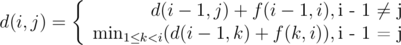Задача А (Div-2). Игрушечные армии
Утверждение первое: пусть пусть первым ходом было убито x солдат, а вторым y, тогда третьим ходом количество убитых будет равно min(n - x, n - y) = n - max(x, y). Значит, общее количество убитых будет равно x + y + n - max(x, y) = n + min(x, y), и именно эту величину нам нужно максимизировать. Рассмотрим ограничения на эти переменные: 0 ≤ x ≤ n, 0 ≤ y ≤ n - x. Значит, нам нужно найти максимум функции f(x, y) = n + min(x, y) в этой области. Понятно, что если мы скажем, что y = n - x (то есть для y примем крайнее положение), то ответ не уменьшится, а значит, можем свести нашу функцию к f(x) = n + min(x, n - x) на отрезке [0, n]. Очевидно, максимум этой функции равен 3· n / 2 в точке x = n / 2.
Ответ: 3· n / 2.
Задача E (Div-1). Две последовательности
Для начала, попробуем нашу задачу решить, не задумываясь об асимптотике. Рассмотрим динамическое программирование, где состояние - это пара (i, j) (а значение - это минимальная суммарная длина двух последовательностей), которое означает, что первая последовательность у нас заканчивается строкой i, а вторая - строкой j. Переходы тогда выглядят следующим образом: мы должны взять элемент с номером v = max(i, j) + 1 и добавить в одну из последовательностей, таким образом перейти в новые состояния (i, v) и (v, j), пересчитав нужным образом значение.
Выпишем более формально, но теперь использовав динамическое программирование "назад", считая, что i > j:
Теперь придумаем окончательное решение. В силу постановки нашей задачи, можно задачу свести к другой динамике - D(i, s), где состояние означает, что одна из последовательностей заканчивается на строку номер i, а вторая - на саму строку s, причем, заметим, что под строкой s будем подразумевать не только строки из входных данных, но и все их суффиксы длиной от 0 до l. Вспомним, что строки у нас бинарные длиной не более 20 символов, а это значит, что строки можно закодировать двоичными числами, в этом случае строка кодируется парой - длиной и самим числом (это строка, если ее интерпретировать как двоичную запись; эта тонкость нужна, т.к. в строках, возможно, присутствуют лидирующие нули, в этом случае разные строки будут переводится в одно и то же число), причем, общее количество пар будет не более 221.
Будем итерироваться по i и поддерживать наш массив со значениями динамики (одномерный, размером 2l). При переходе, нам нужно обновить его в соответствии с формулами выше: по первой нам нужно ко всем элементам массива прибавить величину f(i - 1, i) - это можно сделать, поддерживая дополнительную переменную balance и прибавлять к ней (таким образом, реальное значение элемента i будет равно balance + d[i], хотя в самом массиве значение хранится будет d[i]). А второе обновление еще проще, мы должны перебрать какой длины у нас будет наложение строки на последовательность, взять соотвествующее значение в массиве, и по всем таким перебираемым величинам взять минимум и записать его в соответствующее место в массиве.
Реализовать этот алгоритм можно за асимптотику O(n * l) с требуемой памятью O(n + 2l).