In one problem I was doing, I was getting WA because of some modulo error. In particular, I had a cumulative frequency array which I had defined as:
cf[i]=cf[i-1]+f[i];where f[i] was always positive.
Later, there was a sequence of range queries to answer, so I did:
cout << cf[r]-cf[l-1] for each query; L, R were the range boundaries (both inclusive).
However, the problem stated to report the answer modulo 1000000007, so I changed my queries to:
cout << (cf[r]-cf[l-1]%MOD)%MOD;.
But on seeing the intended solution, I saw that the correct query was :
cout<<(cf[r]-cf[l-1]+MOD)%MOD;
I am unable to understand this, because what I knew was that (a-b)%m = (a%m-b%m)%m
Can please someone explain this to me?
Thanks!! Any help is appreciated.











If (a-b) < 0 then (a-b) % m fails (in C++). (cf[r]-cf[l-1]%MOD) can fail if cf[r] < (cf[l-1]%MOD).
PS: On the other hand you mentioned that the sequence is increasing (which means cf[r] > cf[l-1]). Another place why it failed can be that you need to apply MOD operation on each step, not only when printing the answer, because int overflow can occur.
in maths:(a-b)%m==(a%m-b%m)%m
(10 - 8)% 3 = 1while10%3 - 8%3 = -1. Actually, for a > = b and a, b, m > 0,(a-b)%m = (a%m - b%m + m)%mi think(10-8)%3=1, really? Lolwut?
1+1=10 isn't it :D
In lots of programming languages, a negative number modulo something will be negative. For example, -1 mod 5 would return -1 in many languages. Since we are taking a modulo, we know x%m = (x+m)%m. Therefore, by adding mod, we always make x positive, and so our modulo should behave as expected.
For mod operation you can always do the following:
(a+b) mod m = (a+b+m)%mSo this formula will work for negative and positive values, but you have to be careful about the overflow.
Another way: If you know that
aandbless than m you can apply this:And this is even faster than the first formula.
First of all, I believe that your calculation of
cflooked like this:cf[i] = (cf[i - 1] + f[i]) % MOD;Otherwise your solution is probably wrong, because you have integer overflow. Moreover, integer overflow in signed types (likeint, but notunsigned int) is undefined behavior, that is, your program can do anything if that happen (formally, it can even wipe your hard drive). Don't worry — usually you just get strange wrong answer or runtime error.I don't get what is the reasoning behind writing
(a - b % MOD) % MODinstead of(a - b) % MOD. Would you mind explaining?About the reference solution: you see, if we define reminder as a number from 0 to MOD - 1, then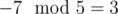 . However, it's not like some CPUs work and if you calculate
. However, it's not like some CPUs work and if you calculate  in C++ on a typical PC, you will most likely get - 2. It's correct in some sense, but it's not what "reminder" means in most problems. So, when you deal with negative numbers or subtractions modulo MOD, you should be careful be negative results. Say, writing
in C++ on a typical PC, you will most likely get - 2. It's correct in some sense, but it's not what "reminder" means in most problems. So, when you deal with negative numbers or subtractions modulo MOD, you should be careful be negative results. Say, writing
(a - b) % MODis unsafe even if both a and b are correct non-negative remainders, becausea - bcan be negative and the whole result would be wrong. However, if we write(a - b + MOD) % MODthen the whole expression on the left would be non-negative and we will get correct result (if there were no integer overflow, of course).Thanks for the reply.
Yes, you are right, I declared cf array as
cf[i]=(cf[i-1]+f[i])%MOD;However, I know for sure that cf does not overflow (there is a solution that does not take modulo to compute it).
I tried both (a%m-b%m)%m and (a-b%m)%m but they did not pass.
Here is the problem links:
http://imgur.com/al93dIH http://imgur.com/79eUkEO
Author’s solution: https://code-snip.herokuapp.com/paste?-JxM86eirwK4RQIP2zsb One of my solutions: https://code-snip.herokuapp.com/paste?-JxU2ly2pqABhLzCcxlB
I've always believed that the reason a%b is negative when a is negative is that we want to maintain the invariant: a = a/b*b + a%b
That is half of the reason. Other half is the way division result is rounded. Rounding towards 0 results in negative values, but rounding down would result in positive values.
- 5 = - 1·3 - 2 rounding to 0
- 5 = - 2·3 + 1 rounding down
Interesting fact, until c++11 direction of rounding (and as a result modulo value) was implementation defined, but starting with c++11 it is guaranteed to round towards zero and negative modulo for negative values.