Good day!
I am an author of the problem C in the first round of Yandex.Algorithm competition and I would like to tell you about the solution of this problem.
I hope you enjoyed the problem and regret about the weakness of the test-set. This trouble was mentioned by the user maksay, whose quadratic solution is successfully passed system tests. I did not consider this case when created tests for the problem and random tests with deep trees could not challenge this solution.
So, let remember statement of the problem. We have the correct binary search tree and the set of request keys. For each request key we consider paths in the tree with one error. These paths are constructed by the search of request key in the tree with one wrong choice of the next vertice. Each wrong choice generate one search path in the tree.
At the beginning solve the problem for one request key. Consider the vertex of the path, after which the error occurred. Suppose that correct search at this vertex goes to the left child but we go to the right. This means that request key lies in key range of the left subtree and we go to the right subtree. Therefore further search of request key goes to the vertex of the right subtree with minimum key. Similar, if correct search goes to the right child but we go to the left, then further search goes to the vertex with maximum key in left subtree.
Count maximum and minimum keys for each subtree of the all tree. This is done by the depth-first search. If we know minimum and maximum keys for all subtrees, there is easy to count answer for given request key. Execute search of the request key and accumulate values of minimum or maximum keys of subtrees where we go with one error.
Now solve the problem for all request keys. Note that the answer for request key depends of only final vertex of the correct search in the tree. Therefore count answer for all leafs of the tree by one depth-first search. For all request keys we need to find final vertex of the search very fast. Put all keys of all vertices of the tree in ordered array. Note that keys of inner vertices and keys of leafs are alternated in this array. So, for each request key find nearest left and right keys in this array using binary search. One of this keys belongs to the leaf. Answer for this leaf would be answer for given request key.
Thus, solution of the problem requires two depth-first searches and k binary searches in array. So, running time is 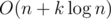 , where n is a number of vertices in the tree and k is a number of request keys.
, where n is a number of vertices in the tree and k is a number of request keys.
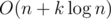 , where n is a number of vertices in the tree and k is a number of request keys.
, where n is a number of vertices in the tree and k is a number of request keys.










`