ACM-ICPC Japanese Alumni Group Summer Camp 2015 Day 4. The problem set was also used in Open Cup GP of Japan.
In short,
- Using Chinese Remainder Theorem, and solve the equation in each pe where
 .
. - Combine the results.
More precisely,
The problem is, "For given N, find the minimum positive integer k, such that for all 0 < a < N, 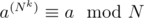 ."
."
For a prime p, 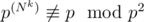 . Thus, if p2 is a divisor of N for some p, then the answer is "-1" (which means there is no such k).
. Thus, if p2 is a divisor of N for some p, then the answer is "-1" (which means there is no such k).
Now, we can assume that N can be represent as p1 * p2 * ... * pr, by some distinct prime numbers pi. (That is, N is square-free number.)
From the Chinese Remainder Theorem, the answer k is the minimum positive integer, such that for all i and for all 0 < a < pi,  .
.
From the well-known theorem called "Fermat's little theorem", such k is the minimum positive integer, such that for all i, 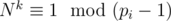 .
.
Now, we'll fix some i, and determine the constraints of k by solving the formula "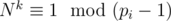 ".
".
Of course, if 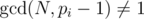 , then there are no such k. (So, the answer is "-1".)
, then there are no such k. (So, the answer is "-1".)
Otherwise, such k is the multiplies of di, where di is the "Multiplicative order of 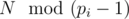 ".
".
That di is a divisor of φ(pi - 1), where φ is the "Euler's totient function". (You can also use the "Carmichael's lambda function" instead of Euler's totient function.)
Now, we want to determine minimum positive integer k, such that for all i, k is the multiply of di. This is of course 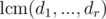 .
.
Summarizing the above,
- Factorize N into p1 * ... * pr, and check whether it is square free.
- For each pi, check
 .
. - For each pi, calculate the di by brute force on the divisors of φ(pi - 1) (or, λ(pi - 1)).
- Report
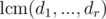 .
.
The sample implementation is available in here: http://jag2015summer-day4.contest.atcoder.jp/submissions/495773










