Hi everybody! It was my first experience of writing problems for TopCoder SRM, hope you liked it. I was a writer of Easy and Medium task in both divisions, subscriber was an author of both Hard tasks. In div1 they were harder than usual, but I hope you still liked them.
Div2 easy
This task was just about implementing exactly what is described in the statement. Looks like Python has a built-in support of set comparison. Usually coders using Python have a disadvantage, but in this task it looks more like an advantage :) There are built-in functions for sets in C++ and Java too, I recommend to learn about them even if you successfully submitted this problem.
Div2 medium
Knowing strings a and b, we can build a reverse mapping q[d] = c, that maps the encoded letter d to it's original corresponding letter c. For letters that do not appear in b, we remember that we don't know their pre-image. After that, we just apply our mapping q to a string y. If some of letters doesn't have a pre-image, we should return "", otherwise we return q(y).
There is an only special case that appears in sample tests: if we know pre-images of all letters except one, we may still uniquely understand what is its pre-image: it is the only letter that doesn't appear in string a.
Div2 hard
This task is an easier version of Div1-hard. In this version it was enough to write a BFS on a graph of all possible states. In this task the state is a set of all already people. Each set can be represented as a binary masks no larger than 218 = 262144 that is small enough to fit in TL.
Div1 easy
A first solution coming to a head works in 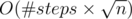 : all we need is to just simulate the process. Suppose we are now standing in number n, the last hour was h, it means that we need to find a first divisor of n or n - 1 larger than f and perform n + + or n – depending on whose (n or n - 1) divisor appears first. Although, one can build a test where number of steps is ~2000, it makes this solution pretty hard to fit in time limit, one of such tests is a last sample test.
: all we need is to just simulate the process. Suppose we are now standing in number n, the last hour was h, it means that we need to find a first divisor of n or n - 1 larger than f and perform n + + or n – depending on whose (n or n - 1) divisor appears first. Although, one can build a test where number of steps is ~2000, it makes this solution pretty hard to fit in time limit, one of such tests is a last sample test.
The key observation is that when we change our number, we don't need to find divisors of a new number from scratch. The well-known divisor finding algorithm consists of two stages: first we consider all divisors smaller than  , then all divisors larger than
, then all divisors larger than  . If we were on the first stage, then we just need to continue iteration from the same place for a new number. If we are on the second stage, we also continue iterating the second stage with a new number. This works in
. If we were on the first stage, then we just need to continue iteration from the same place for a new number. If we are on the second stage, we also continue iterating the second stage with a new number. This works in  since our number can't infinitely increase (it can be shown that it can't move further than 2n, actually it doesn't move further than 100).
since our number can't infinitely increase (it can be shown that it can't move further than 2n, actually it doesn't move further than 100).
The other solution was to cache the divisors for all values of n that happen during the execution.
Div1 medium
The first observation is that an almost-Eulerian graph can be obtained from a unique Eulerian graph. Indeed, if we have an almost-Eulerian graph G that is not Eulerian, then there exists the only pair of vertices u and v that have an odd degree, the only possible original Eulerian graph G' is 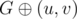 (here
(here  means inverting the specific edge, adding it or removing it). If G is Eulerian itself, then we obviously can't invert some edge keeping it being Eulerian.
means inverting the specific edge, adding it or removing it). If G is Eulerian itself, then we obviously can't invert some edge keeping it being Eulerian.
This means that if there are En Eulerian graphs, then there are exactly 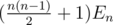 almost-Eulerian graphs: each Eulerian graph G produces itself and all possible
almost-Eulerian graphs: each Eulerian graph G produces itself and all possible 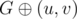 as almost-Eulerian graphs.
as almost-Eulerian graphs.
Now we need to calculate number of Eulerian graphs on n vertices, En. It's well-known that the graph is Eulerian iff it is connected and all its vertices have even degree. The good idea is to first calculate Dn, the number of graphs with all even degrees. If we succeed in it, we can then calculate En by using inclusion-exclusion principle on Dn.
How many even graphs on n vertices are there? The simplest way to understand that is to remove some vertex from it (let's say, a vertex 1) and notice that the graph on remaining vertices 2, ..., n may contain an arbitrary set of edges. Indeed, if there are some odd vertices among them, then when we return vertex 1 back to the graph, we have to connect it to all odd vertices among 2, ..., n. After that all 2, ..., n become even vertices, and 1 itself also becomes even due to handshake lemma. So, the answer is 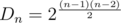 since there may be any possible set of edges between vertices 2, ..., n and all edges from 1 to the rest of the graph may be uniquely determined.
since there may be any possible set of edges between vertices 2, ..., n and all edges from 1 to the rest of the graph may be uniquely determined.
Now how to calculate En. We know that En = Dn - Rn where Rn is number of disconnected even graphs. Suppose that the connected component that contains vertex number 1 consists of k vertices (obviously, 1 ≤ k ≤ n - 1). Then there are 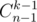 ways to choose k - 1 vertices in this connected component from n - 1 remaining vertices, also there are Ek ways to organize a connected component that has all even degrees and there are Dn - k ways to organize an even graph on the rest of the vertices (note that it may possibly be disconnected if there were 3 or more components in the original graph, that's why we use Dn - k but not En - k here). So, there is a recursive formula:
ways to choose k - 1 vertices in this connected component from n - 1 remaining vertices, also there are Ek ways to organize a connected component that has all even degrees and there are Dn - k ways to organize an even graph on the rest of the vertices (note that it may possibly be disconnected if there were 3 or more components in the original graph, that's why we use Dn - k but not En - k here). So, there is a recursive formula: 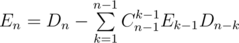 that leads us to an O(n2) DP solution.
that leads us to an O(n2) DP solution.
Div1 hard
I'll describe an approach for this problem very briefly.
What we actually need in this task is to understand how the described process works. We can describe the process in following way. The detective acts almost like a Prim's algorithm: in each step he adds one of the maximal edges between the already visited set and the rest of the vertices in the graph. The only thing that we may adjust is an order of choosing the edges with the equal cost.
At any moment the visited vertices form some part of a maximum spanning tree. Suppose we want to get to vertex x in minimum number of steps. Consider the resulting path between 0 and x. It is a well-known fact that the minimum edge on this number is uniquely defined and is equal to a maximum possible minimum edge among all paths from 0 to x. Suppose the value of this edge is equal to d. We can calculate d by running a Floyd algorithm modification for metric d(u, v) = minimum on path between u and v, that is needed to be maximized.
There are edges of two kinds on a path from 0 to x: those who are equal to d and those who are larger than d. In any situation we prefer larger edges, so when we touch a vertex with some outgoing edges larger than d, we will greedily first visit all those edges. So, let's contract all components connected by edges larger than d.
After contracting all we need is to find a shortest path from 0 to x remembering that each time we visit a vertex, we have to add a size of its connected component described above.











How do you prove that the number can move at max 100 ? My idea was to find divisors for [n-500 , n + 500] , but I didnt submit since I couldnt find a proof for this. I came up with this since it was the easy ques and this approach fit the time limit :P
I can't prove 100, but simple proof that it doesn't move more than 354: before 10^10 there is always at least one prime in every group of 354 consecutive numbers (see wikipedia for prime gaps), and the task will never leave to the right of a prime number.
OK, now it's correct :P
Nice, thanks!
That's an experimental result, although there is an empirical argument that it can't walk further than the average number of divisors of an integer <= 10^12. There are no more than ~2000 divisors for numbers in that range, so it won't walk on a big distance.
Suppose P is the minimum prime just greater than or equal to n. Now the number can't go beyond P and nearest prime will be at a distance of at most 100. isn't it ?
ohh sorry, it's 354 actually.
Thank you for the fast editorial!
What is the maximum number of steps in Div1 250, both theoretically and in the actual test set?
The 5587021440 from examples is 2047 steps.
I managed to find 9777287520 with 2303 steps (I think) but falied to make that a successful challenge.
The numbers that produce the highest number of steps are actually located around the highly composite numbers, so there were several tests (including that you listed) including the one you listed. I don't have a theoretical proof for that fact other that "well, we need to make it hang around the number with many divisors because the divisor function rarely has consecutive high values".
As far as I remember, the number you mention has the maximum possible number of steps.
According to my solution statistics, such tests were not actually included. There are 6983776805 with 1969 steps and 5587021440 with 2047 steps, all others are below 1000. So, the maximal test, in this sense, was not present at all, and the maximal test that was present was in the samples.
Here are the program, input and output I used to check that.
What are the upper bounds of number of all steps and number of steps that we need to compute divisors?
Out of all the reasons why I could fail system test on div1 250...
It turns out I read the example too fast and as a result, I read it wrong.
For some reason I thought "oh yes, employees 2, 3, 4 are not involved in any swaps, and this sample is just giving me 3 free answers, let's hardcode this in so we don't have to think about corner (small) cases".
Oops, lost 69 rating because I tried to save 2 seconds of doing examples by hand.
The bulk of Div1 500 (the number of labeled Eulerian graphs with n nodes) is http://oeis.org/A033678. The first few pages of Graphical Enumeration book mentioned there contain the solution, too.
Personally, I appreciate having to learn how to solve it, it's beautiful. Still, I am a bit surprised that the “almost” condition was considered enough to make it a Div1 500.
We judge the difficulty from how hard to get the idea, instead of how complicated the solution is.
When we preparing SRM670, subscriber suggest to use Tdetective (today's Hard) as Medium. We thought that task is a bit harder for that slot, he argued: "How can it be a Hard since it is just one dijkstra?" but it turns out no one solve it during today's contest.
Today's Medium have a success rate about 10%, so that is hard enough.
What I am saying is not that the solution is difficult to implement but that the major part of it (namely, the number of labeled Eulerian graphs with n nodes) is easy to Google.
For Div1 Medium there should be Ek in the recurrent formula in the last sentence.
I had a different idea for Div 1 easy.
I can't figure out why "the minimum edge on this number is uniquely defined and is equal to a maximum possible minimum edge among all paths from 0 to x". Sorry for my superficial experience.