593A - 2Char
For each letter will maintain the total length of words (cnt1ci), which found it was alone, and for each pair of letters will maintain the total length of words that contains only them (cnt2ci, cj).
For each row, count a number of different letters in it. If it is one, then add this letter to the length of the word. If two of them, then add to the pair of letters word`s length.
Now find a pair of letters that will be the answer. For a pair of letters ci, cj answer is cnt1ci + cnt1cj + cnt2ci, cj. Among all these pairs find the maximum. This is the answer.
The overall complexity is O (total length of all strings + 26 * 26)
593B - Anton and Lines
Note that if a s line intersects with the j th in this band, and at x = x1 i th line is higher, at x = x2 above would be j th line. Sort by y coordinate at x = x1 + eps, and x = x2 - eps. Verify that the order of lines in both cases is the same. If there is a line that its index in the former case does not coincide with the second, output Yes. In another case, derive No. The only thing that can stop us is the intersection at the borders, as in this case we dont know the sorts order. Then add to our border x1 small eps, and by x2 subtract eps, and the sort order is set uniquely. The overall complexity is O(nlogn)
593C - Beautiful Function
One of the answers will be the amount of such expressions for each circle in the coordinate x and similarly coordinate y: 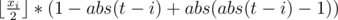
For a = 1, b = abs(t - i), it can be written as 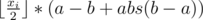
Consider the a - b + abs(a - b):
if a ≤ b, то a - b + abs(a - b) = 0,
if a > b, то a - b + abs(a - b) = 2a - 2b
Now consider what means a > b:
1 > abs(t - i)
i > t - 1 and i < t + 1.
For integer i is possible only if i = t.
That is, this bracket is not nullified only if i = t.
Consider the 2a - 2b = 2 - 2 * abs(t - i) = 2. Then 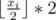 differs from the wanted position by no more than 1, but since all the radiuses are not less than 2, then this point belongs to the circle.
differs from the wanted position by no more than 1, but since all the radiuses are not less than 2, then this point belongs to the circle.
The overall complexity is O(n).
593D - Happy Tree Party
Consider the problem ignoring the second typed requests. We note that in the column where all the numbers on the edges of > 1 maximum number of assignments to 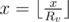 before x will turn into 0 is not exceeds 64. Indeed, if all the Rv = 2, the number of operations can be assessed as log2(x). Hang the tree for some top and call it the root.
before x will turn into 0 is not exceeds 64. Indeed, if all the Rv = 2, the number of operations can be assessed as log2(x). Hang the tree for some top and call it the root.
Learn how to solve the problem, provided that for every v Rv > 1 and no requests of the second type. For each vertex except the root, we have identified it as the ancestor of the neighbor closest to the root. Suppose we had a request of the first type from the top a to b vertices with original number x. We divide the road into two vertical parts, one of which is close to the root, while the other moves away. We find all the edges in this way. To do this, we calculate the depth of each node to the root of the distance. Now we will go up in parallel to the tree of the two peaks, until he met a total. If in the course of the recovery, we have been more than 64 edges, in the substitutions 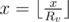 we get x = 0 and we can at the current step to stop the algorithm search. Thus, we make no more than O(log(x)) operations.
we get x = 0 and we can at the current step to stop the algorithm search. Thus, we make no more than O(log(x)) operations.
Let`s turn to the problem, where Rv > 0. We note that our previous solution in this case can work for O(n). Since the passage of the edge with Rv = 1 our value does not change. We reduce this problem to the above consideration. Compress the graph, that is, remove all single edges. To do this, run by dfs root and will keep the deepest edge on the path from the root to the top with Rv > 1.
Let us remember that we have had requests to reduce Rv. We maintain the closest ancestor of Pv c RPv > 1. We use the idea of compression paths. When answer to a request of the first type will be recalculated Pv. We introduce a recursive function F(v). Which returns the v, if Rv > 1, otherwise perform the assignment of Pv = F(Pv) and returns F(Pv). Each edge we will remove 1 times, so in total the call of all functions F(v) running O(n).
Final time is O(logx) on request of the first type and O(1) an average of request of the second type.
593E - Strange Calculation and Cats
Learn how to solve the problem for small t. We use standard dynamic dpx, y, t = number of ways to get into the cell (x; y) at time t. Conversion is the sum of all valid ways to get into the cell (x; y) at time t — 1.
Note that this dp can be counted by means of the construction of the power matrix. Head of the transition matrix, Ti, j = 1, if we can get out of the cell i in a cell j. Suppose we had a vector G, where Gi equal to the number of ways to get into the cell i. Then a new vector G' by dt second G' = G * (Tdt).
So we learned to solve the problem without changes in O (log dt * S3), where dt — at a time, S — area.
Consider what happens when adding or removing a cat. When such requests varies transition matrix. Between these requests constant T, then we can construct a power matrix. Thus, at the moment of change is recalculated T, and between changes in the degree of erecting matrix. The decision is O (m * S3 log dt), m — number of requests











Auto comment: topic has been translated by josdas (original revision, translated revision, compare)
B: There is no need to use eps, if the equal Y1 to sort by Y2(and Y2 by Y1). So all numbers will be int instead of double.
I don't think your solution on E is fast enough :P
How long does it take your solution to run on this test?
It seems that on all of their big testcases time makes big jumps and then increases very little for a while. So the logarithm part is almost always 1.
I wrote a solution which passed their tests in 870ms, but worked on my custom testcase with t[0] = 100000, t[1] = 200000, t[2] = 300000 etc. for 18 seconds.
I still managed to pass that testcase in a bit under 3.5 seconds using the fact that we can take modulo once or maximum twice during 20 multiplications in the third loop of the exponentiation. But the constraints are definitely too big for the solution and the testcases are weak =)
But it will be terrible if author's solution can't pass those tests (Eg. the test I posted in my above comment.)
I regret not coding this solution. I should have coded it, locked and tried hacking others with that test. I wonder which verdict I would received. :P
Didn't see your edit when I replied. We came up with the same thing :D
By the way, differences of 65535 are even better than 100000, they lead to more matrix multiplications. Almost all accepted solutions fail such testcases.
I can barely pass this case, just in time, 3977 ms :)
Contest như cl :)
Please write in English for everyone to understand. Thank you.
Wow, C solution is awesome. And the question too.
For problem B, I think that there's no need to use EPS. The announced message during the contest maybe lead contestants the wrong ways.
My solution is all using int. In general, a Line
Y = a * X + b, because[a, b]are Integers,[X1, X2]are also Integers, so we can sure that[Y1, Y2]are Integers either.So now you have
([Yi1, Yi2]), sort that array.Two lines (i, i + 1) are intersected strictly in range(X1, X2) must have a order that
Yi1 <= Y(i+1)1andYi2 >= Y(i+1)2. Because all lines are distinct, so these pairs are not identical.Remember to use long long int.
I can't realize the fact that only the lines yi and yi+1 will intersect, Even after sorting. Any of the lines could intersect. Can you elaborate a little?
Let me help you.
Let's suppose you have all the lines sorted in Y1 ascending order.
I will refer to the lines as to their Y1 and Y2: Let's suppose we have,in this order,lines [Y11,Y12],[Y21,Y22],[Y31,Y32] and so on.(Therefore Y31>Y21>Y11,etc)
Your question was why we only need to do the process for the consecutive lines,right? Let's suppose that we have no such two consecutive lines.
Therefore,let's suppose lines 3 and 2 don't intersect but 3 and 1 do.That means that we have already checked lines 2 and 1 and they don't intersect,also.
Well then,3 and 1 intersecting means Y31>Y11 and Y32<Y12
Lines 3 and 2 not intersecting means Y31>Y21 and Y32>=Y22.
But that would mean Y12>Y32>=Y22,and Y11<Y21 since that's how we sorted;
That means lines 1 and 2 intersect. But we supposed there are no two consecutive lines to intersect.Contradiction.
That should be it,please message me if you need further help.
What hard contest ! :)
The problem D also solvable with LCA and Heavy Light Decomposition. I have solved it with this method.
Can you explain your solution please?
i choose 1. node root of tree. in heavy light the people use segmenttree on nodes.
but in here, i have edges not nodes. then convert edges to nodes. convert the edge, a node which is one of both nodes of edge and more under then other one. (in here i want to tell you make segmenttree on edges. just it)
example :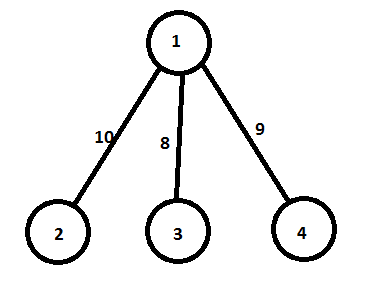
the segmenttree's [2] = 10, [3] = 8 and [4] = 9;
other codes is same as heavy. also to answer queries i find LCA.
i had a problem with overflow. multiply integers with a function which returns 10e18+1 if multiplication bigger than 10e18+1.
Answered.
I just solved D with HLD, in this 14087878 — I handled overflow like this —
which gave WA at 37. When I replaced this with (14087899)-
AC. Can you please tell me why? If overflow happens, shouldn't (x*y) be smaller than x or y?
no. it doesnt have to be smaller than x or y.
Computer handle the multiplication overflow by simply cut the higher bits off. So we couldn't make sure that after cutting off the higher bits, x*y will be smaller than x or y.
However signed integer overflow is undefined behaviour. Compiler can optimize it aggressively and you can't predict what would happen. To be precise, GCC would assume that there is no overflow of signed integers. So it could optimize expression
x * y < xto maybex > 0 ? (y < 1) : (y > 1)which is more fast.Replace
long longwithunsigned long longwould work if MisakaMisakaMisaka ' analysis is correct.Read this for more information.
I discuss with my friend about Problem B , then I found three different ways to solve : 1.I adopt which as same as Tutorial. 2.Zhang make a little change with "sort" , just raplace the "x1 += eps , x2 -= eps" : ~~~~~ struct Line{ int yl, yr, k, b; }l[N];
bool cmp(Line a, Line b){ if(a.yl == b.yl) return a.yr < b.yr; return a.yl < b.yl; } ~~~~~ 3.Bao found that if there is a intersection , then adjacent lines must will make . so just sort , then judge in turn . =_= ...
Cannot understand the solution of the problem D properly. :/
Can someone make it simple and explain?
u should know that floor(floor(x/m)/n) = floor(x/mn). Hence u just need a segment tree to maintain the product of a segment. And since we do this on a tree, heavy-light decomposition is needed.
Thanks. This problem is solved by LCA-DSU by many of the other coders. I checked the solution of waterfalls and it was pretty understandable.
Can somebody explain the approach used
but the product will become too big to be stored in any integer datatype. How do I handle that?
you can use (a*b)/b==b to check whether there is overflow. And if there is, just set the product's value as 1e18 or other big value.
Answered.
For each node i, we simply maintain fa[i], which means the deepest node on its path to root, whose Rv > 1. For the first type of query, we just walk up through the array fa[] and update the value of y (as other edges are useless) , and we at most walk for 64 times. For the second query, after changing the value of Rv to 1, we need to change fa[v] to its father's fa[] (this node is no longer useful). Just like dsu, we will compress the path while visiting these nodes.
You can have a look at my solution 14098546.
What goes on B when we sort Y1 and Y2 in a vector of pairs then check, why do we have to sort them individually ?
What's the intuition for C ? How do you arrive at such an expression?
This is how I came up with my solution.
I ignored all this bla-bla-bla about points being inside or on the border of circles and tried to solve similar problem for points being exactly at the centers of the circles. This condition is stricter than the original one (and might be unsolvable), but if we solve this one, we solve the original one. So I was looking for functions f(t), g(t), such that: f(1) = x[1], g(1) = y[1] f(2) = x[2], g(2) = y[2] ... f(N) = x[N], g(N) = y[N]
Now we can forget that we have 2 different functions f(t) and g(t), and try to solve it only for f(t) and x[1..N]. If we solve it for f(t) and x-coordinates, we will apply the same logic to g(t) and y-coordinates.
The definition and some examples of "correct" functions should tell us that we can generate almost any "saw-looking" function. What is "saw-looking"? Well, not easy to define properly, but here is an example of graph for "abs(5-abs((1-abs(x-1))))-2": https://www.google.com.sg/webhp?ion=1&espv=2&ie=UTF-8#safe=off&q=abs(5-abs((1-abs(x-1))))-2
We can generate a bunch of saw-functions just by changing the coefficients and number of "abs" functions.
Let's forget for now about functions like "x*x" which are also "correct", but these are parabolas, and let's have our fingers crossed we will not need these to solve our problem.
Can we find such "saws", that f(1) = x[1], ..., f(N) = x[N]? My first idea was to generate "saws", such that fK(t) = 0 for all t < K. If we can find such saws, we are almost good to solve the problem. I think I saw a solution that implemented this idea, but I gave up during the round and tried to find something else.
What if find magical fK(t), such that fK(K) = x[K], and fK(t) = 0 for all t != K. If we do this, our problem is solved. When we calculate f(t) = f1(t) + ... + fN(t), all numbers fi(t) will be equal to 0 but one. And f(t) will be equal to ft(t), which will be equal to x[t]. Bingo!
Now we need to find magical fK(t). Interesting observation. If we have saw-looking function s(t), we can generate function s(t) + abs(s(t)), which will be a doubled saw if s(t) >= 0, and zero if s(t) < 0. For example, abs(5-abs((1-abs(x-1))))-2 + abs(abs(5-abs((1-abs(x-1))))-2): https://www.google.com.sg/search?q=abs(5-abs((1-abs(x-1))))-2+%2B+abs(abs(5-abs((1-abs(x-1))))-2)&oq=abs(5-abs((1-abs(x-1))))-2+%2B+abs(abs(5-abs((1-abs(x-1))))-2)
That's where the magic happens. If we take a function 1-abs(t-k), and apply this magic transformation, we will get a function that is equal to 2 if t = k, and equal to zero otherwise.
We are almost there! If we define fK(t) = (1-abs(t-K)) + abs((1-abs(t-K))), and slightly adjust a formula for f(t), we will get the following: f(t) = f1(t)*x[1] + f2(t)*x[2] + ... + fN(t)*x[N] f(1) = 2*x[1] ... f(N) = 2*x[N]
What should we do about this "2"? If x[k] is even, we will just divide x[k] by 2 in the definition of f(t): f(t) = f1(t)*x[1]/2 + f2(t)*x[2]/2 + ... + fN(t)*x[N]/2
But what if x[K] is odd?
This tells us that this definition will work even for odd values: f(t) = f1(t)*x[1]/2 + f2(t)*x[2]/2 + ... + fN(t)*x[N]/2
f(t) will be equal either to x[t] or x[t]-1.
Solved!
In DIV2 B , sorting vector<pair<double,double> > gives TLE while vector<pair<long long,long long> > gives AC ... Can someone explain why this is happening?
Because use scanf() or sync_with_stdio(false). Read the 10^5 double numbers is quite long.
http://codeforces.com/contest/593/submission/14093632
By the way, you have a bag with for(int i = 0; i < n; i++), because when you use v[i + 1] you get vector index out of bounds, but i have no idea why you passed test 8, and my resubmite don't.
http://codeforces.com/contest/593/submission/14093538
P.S. So many local variables...
http://codeforces.com/contest/593/submission/14179073
Problem D I don't know Why I have a wrong answer on test 15. I have found the mistake for 3 days but I can't :( Help me :(((
I used heavy light decomposition.
Why I always get TLE of problem D Happy Tree Party in Test 13?