A div2. In this problem you can simulate the process. You can consider all minutes and in dependence by a color of a current cablecar decrease size of corresponding group of students G by min(|G|, 2), where |G| is size of the group. After that you should determine the first minute t in that all three groups of students will be empty. So t + 30 is an answer. This solution works in O(r + g + b).
Also there is O(1) solution. It is following formula: ans = max(3[(R + 1) / 2] + 27, 3[(G + 1) / 2] + 28, 3[(B + 1) / 2] + 29) where [x] is rounding down.
B div2. It this problem you should write exactly that is written in statement. For every letter you should see a row and a column of the letter. If equal letter was found, current letter sould not be output. You can combine scanning rows and columns and output an answer, for example, this way:
FOR(a,1,n) FOR(b,1,m)
{
bool should_out=true;
FOR(c,1,n) if (c!=a) if (T[a][b]==T[c][b]) should_out=false;
FOR(c,1,m) if (c!=b) if (T[a][b]==T[a][c]) should_out=false;
if (should_out) printf("%c", T[a][b]);
}
This solution works in O(mn(n + m)).
Also here an O(nm)-solution exitsts. In every row and column you can calculate a number of every letter of an alphabet. After that check for output can be done in O(1). You just should check that numbers of entries of considered letter into corresponding row and column equal exactly 1.
C div2 и A div1. Determine a form of all arrangements of diamonds that set of all sums of pairs adjacent cells is invariably. If you remove from the first cell exactly c diamonds, you should add exactly c diamonds into the second cell, remove c diamonds from the third cell and so on. In other words, all valid arrangements can be produced by adding c diamonds into every even cell and removing c diamonds from every odd cell, where c is some integer. c lies in range from 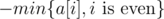 to
to 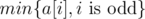 because otherwise number of diamonds in some cell will be less than zero. There is no more valid arrangements.
because otherwise number of diamonds in some cell will be less than zero. There is no more valid arrangements.
Now consider a number of all diamonds in cells as a function of c. If n is even, the sum always is constant. So there is impossible of theft diamonds and answer is 0. For odd n for every c there is c extra diamonds. So, Joe can theft no more than 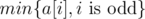 diamonds.
diamonds.
It is easy for undarstanding that for increasing (or decreasing) c by some constant x Joe should do x(n + 1) / 2 moves, but he cannot done it by lass count of moves. In one minute Joe can change c no more than on [m / ((n + 1) / 2)]. Common number of diamonds thet Joe can theft for all time is k[m / ((n + 1) / 2)], but you should take into account a limits for changing of c.
At the end common solution is following: If n is even, answer is 0, otherwise answer is 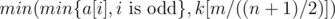 .
.
Be careful fith overflow of 32bit integers. Here you should use an 64bit integers.
D div2 и B div1. Here you can build some miltigraph in which nodes are widgets and edges are relationship of pack()-method. This graph is acyclic. Next, you should do topological sort of nodes. Sizes of widgets should be calculated in the obtained order. At the last, you should sort all nodes by thier names and output an answer.
About implementation.
Parsing of instructions is very easy if you swap charachers '.', ',', '(', ')' by spaces. Now you can just split instructions into strings using spaces as separators.
Multigraph can be saved into matrix. Cell M[i][j] contains integer number that means number of edges from node i to node j. Topological sort can be done by any stupid method. For example, you can choose k times node that has no outgoing edges to unselected nodes, where k is numder of nodes. Every check can be done in O(k2).
You should recalculate sizes of widgets using 64-bit integets (a tip was is statement). In a test like
100
Widget w(100,100)
HBox box
box.pack(w)
box.set_border(100)
HBox a
a.pack(box)
a.pack(box)
HBox b
b.pack(a)
b.pack(a)
HBox c
c.pack(b)
c.pack(b)
...
width of widgets grows exponentially. In jurys' tests maximum length of a side of widgets was 103079215104000. You can get that length by packing 4 widgets everu time instead of 2 widgets.
E div2 и C div1. This problem can be solved by simulation. You can just iterate over all chips and for every of them calculate number of points. But srupid simulate can give O(k3) time solution, where k is total number of chips. It doesn't fit into time limits. For example, try test like
1 5000
RRRR...[2500 times]LLLL...[2500 times]
You can simulate process in 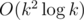 time by using some data structures like std::set, but it doesn't fit into limits too.
time by using some data structures like std::set, but it doesn't fit into limits too.
Similating in O(k2) time is given by following data structure.
For every chip you can save links to chips that is placed up, doun, left and right from the considered chip. Net of links can be built in O(nm). Now, when you simulate process, you can remove chips this way:
Chip->L->R = Chip->R
Chip->R->L = Chip->L
Chip->U->D = Chip->D
Chip->D->U = Chip->U
So, jump from some chip to the next chip in a move can be done in O(1). Now you can simulate every move in O(k).
Remove operation is reversible because every removed chip stores links to all of its neighbours. Therefore you can save links to all removed chips in current move and after restore net of links using following operetions for all removed chips in reversed order
Chip->L->R = Chip
Chip->R->L = Chip
Chip->U->D = Chip
Chip->D->U = Chip
Also you can just build net of links anew for every move.
D div1. Initially lets pump all mines on radius of Death Star and squeeze Death Star into point. Now you should determine an intersection of a ray with obtained figures.
Mine's body with radius r is pumped into ball with radius r + R. Every mine's spike is pumped into union of two balls with radius R and cylinder. One of these balls lies inside of pumped mine's body, therefore you can don't consider it. Let length of spike is r0. Then cylinder will have heigth r0 and radius R. A distance between center of one base of the cylinder and edge of another one equals 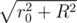 . Following unequation proves that this distance always less than radius of pumped mine's body and cylinder lies inside of the pumped mine's body:
. Following unequation proves that this distance always less than radius of pumped mine's body and cylinder lies inside of the pumped mine's body: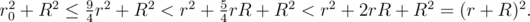
So, you can don't consider the cylinders too. For every spike you should store only ball of radius R with center in a peak of the spike.
Now we have set of balls, we are needed to determine a time in that some point collides with every of those balls. Lets write an equation:
|A + vt - O| = R,
where A is start position of point, v is vector of its velocity, O is center of ball, R is its radius. Lets rewrite equation in scalar variables:
(Ax + vxt - Ox)2 + (Ay + vyt - Oy)2 + (Az + vzt - Oz)2 = R2.
When you expand brackets, you receive some quadratic equation from variable t:
At2 + Bt + C = 0.
You should solve it and choose minimal root (minimal root is time of the first collision of point with the ball, maximal one is time of the second collision). Check than root more than 0.
Now you should determine all times and choose minimum of them. If there are no collisions, answer is -1.
All checking should be done in integer 64bit numbers for absolutely precision.
E div1. Solomon can just create some segments of ice cubes and cut its. Consider a segment with rightmost begin. You can assume that it ends in position of the last demon (you always can cut end of a segment that ends on last demon and add it to current segment). For cutting the last segment you should build "ice bridge" to it. When you are building this bridge, you should create and cut all others segments.
Now iterate over all start positions of the last segment. For every of them you should decrease powers of demons that is covered by this segment and calculate minimal number of moves for destroy all demons (do not forgen about the last segment!).
You can see that for every fallen ice cube you need exactly 3 operations --- go left, create cube, go right. For cutting a segment you need exactly 2 operations --- create cube and destroy one. Therefore all demons should be covered by minimal number of segments that no cube falls on an empty position. It can be done by greedy algorithm.
Total number of operations for every start position of the last segment can be calculated in O(n). Total number of checks is O(n), so we have an O(n2) solution.
After all, answer can be built very easy.










The data structure used in div2 E / div1 C is an extension of Doubly linked list to 2 dimensions, where every node forms a doubly linked list with all the nodes in the same column and another list with all the nodes in the same row.