Problem 0: Richard has been infected with bovine spongiform encephalopathy. Help Kevin understand what he's saying!
Div 2 A
Hint: Just do it! But if you're having trouble, try doing your computations using only integers.
This problem is straightforward implementation---just code what's described in the problem statement. However, floating point error is one place where you can trip up. Avoid it by rounding (adding 0.5 before casting to int), or by doing all calculations with integers. The latter is possible since 250 always divides the maximum point value of a problem. Thus when we rewrite our formula for score as 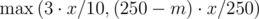 , it is easy to check that we only have integers as intermediate values.
, it is easy to check that we only have integers as intermediate values.
Code: http://codeforces.com/contest/604/submission/14608458
Div 2 B
Hint: Try thinking about a sorted list of cowbells. What do we do with the largest ones?
Intuitively, we want to use as many boxes as we can and put the largest cowbells by themselves. Then, we want to pair the leftover cowbells so that the largest sum of a pair is minimized.This leads to the following greedy algorithm:
First, if k ≥ n, then each cowbell can go into its own box, so our answer is max(s1, s2, ..., sn). Otherwise, we can have at most 2k - n boxes that contain one cowbell. So as the cowbells are sorted by size, we put the 2k - n largest into their own boxes. For the remaining n - (2k - n) = 2(n - k) cowbells, we pair the i th largest cowbell with the (2(n - k) - i + 1) th largest. In other words, we match the smallest remaining cowbell with the largest, the second smallest with the second largest, and so on. Given these pairings, we can loop through them to find the largest box we'll need. The complexity of this algorithm is O(n) in all cases.
To prove that this greedy works, think about the cowbell the the largest one gets paired with. If it's not the smallest, we can perform a swap so that the largest cowbell is paired with the smallest and not make our answer worse. After we've paired the largest cowbell, we can apply the same logic to the second largest, third largest, etc. until we're done.
Code: http://codeforces.com/contest/604/submission/14608465
Div 2 C/Div 1 A
Hint: Is there any easy way to describe the longest alternating subsequence of a string? What happens at the endpoints of the substring that we flip?
Imagine compressing each contiguous block of the same character into a single character. For example, the first sample case 10000011 gets mapped to 101. Then the longest alternating subsequence of our string is equal to the length of our compressed string. So what does flipping a substring do to our compressed string? To answer this, we can think about flipping a substring as flipping two (possibly empty) prefixes. As an example, consider the string 10000011. Flipping the bolded substring 100 00 011 is equivalent to flipping the two bolded prefixes 10000011 and 10000.
For the most part, flipping the prefix of a string also flips the corresponding portion of the compressed string. The interesting case occurs at the endpoint of the prefix. Here, we have two possibilities: the two characters on either side of the endpoint are the same or different. If they are the same (00 or 11), then flipping this prefix adds an extra character into our compressed string. If they are different (01 or 10), we merge two characters in our compressed string. These increase and decrease, respectively, the length of the longest alternating subsequence by one. There is actually one more case that we left out: when the endpoint of our prefix is also an endpoint of the string. Then it is easy to check that the length of the longest alternating subsequence doesn't change.
With these observations, we see that we want to flip prefixes that end between 00 or 11 substrings. Each such substring allows us to increase our result by one, up to a maximum of two, since we only have two flips. If there exist no such substrings that we can flip, we can always flip the entire string and have our result stay the same. Thus our answer is the length of the initial longest alternating subsequence plus  .
.
A very easy way to even simplify the above is to notice that if the initial longest alternating subsequence has length len - 2, then there will definitely be two 00 or 11 substrings. If it has length n - 1, then it has exactly one 00 or 11 substring. So our answer can be seen as the even easier 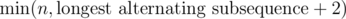 .
.
Code: http://codeforces.com/contest/603/submission/14608473
Div 2 D/Div 1 B
Hint: First there are special cases k = 0 and k = 1. After clearing these out, think about the following: given the value of f(n) for some n, how many other values of f can we find?
We first have the degenerate cases where k = 0 and k = 1. If k = 0, then the functional equaton is equivalent to f(0) = 0. Therefore, pp - 1 functions satisfy this, because the values f(1), f(2), ..., f(p - 1) can be anything in {0, 1, 2, ..., p - 1}.
If k = 1, then the equation is just f(x) = f(x). Therefore pp functions satisfy this, because the values f(0), f(1), f(2), ..., f(p - 1) can be anything in {0, 1, 2, ..., p - 1}.
Now assume that k ≥ 2, and let m be the least positive integer such that 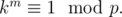 This is called the \emph{order} of
This is called the \emph{order} of  First, plug in x = 0 to find that
First, plug in x = 0 to find that 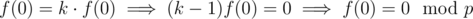 as p is prime, and
as p is prime, and  . Now for some integer
. Now for some integer 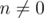 , choose a value for f(n). Given this value, we can easily show that
, choose a value for f(n). Given this value, we can easily show that 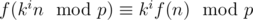 just by plugging in x = ki - 1n into the functional equation and using induction. Note that the numbers n, kn, k2n, ..., km - 1n are distinct
just by plugging in x = ki - 1n into the functional equation and using induction. Note that the numbers n, kn, k2n, ..., km - 1n are distinct  , since m is the smallest number such that
, since m is the smallest number such that 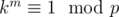 . Therefore, if we choose the value of f(n), we get the value of m numbers (
. Therefore, if we choose the value of f(n), we get the value of m numbers (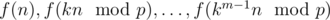 ). Therefore, if we choose f(n) of
). Therefore, if we choose f(n) of 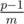 integers n, we can get the value of all p - 1 nonzero integers. Since f(n) can be chosen in p ways for each of the
integers n, we can get the value of all p - 1 nonzero integers. Since f(n) can be chosen in p ways for each of the 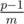 integers, the answer is
integers, the answer is 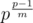 .
.
Another way to think about this idea is to view each integer from 0 to p - 1 as a vertex in a graph, where n is connected to 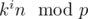 for every integer i. If we fix the value of f(n) for some n, then f also becomes fixed for all other vertices in its connected component. Thus our answer is p raised to the the number of connected components in the graph.
for every integer i. If we fix the value of f(n) for some n, then f also becomes fixed for all other vertices in its connected component. Thus our answer is p raised to the the number of connected components in the graph.
Code: http://codeforces.com/contest/603/submission/14608476
Challenge: How quickly can we find m? For this problem we let O(p) pass, but faster methods certainly exist. (This is a very open-ended question.)
Div 2 E/Div 1 C
Hint: Is there a way to determine the winner of a game with many piles but looking at only one pile at a time?
We'll use the concepts of Grundy numbers and Sprague-Grundy's Theorem in this solution. The idea is that every game state can be assigned an integer number, and if there are many piles of a game, then the value assigned to that total game state is the xor of the values of each pile individually. The Grundy number of a state is the minimum number that is not achieved among any state that the state can move to.
Given this brief intro (which you can read more about many places), we have to separate the problem into 2 cases, k even and odd. Let f(n) denote the Grundy number of a pile of size n. By definition f(0) = 0.
If k is even, then when you split the pile of size 2n into k piles of size n, the resulting Grundy number of that state is  as k is even. Given this, it is easy to compute that f(0) = 0, f(1) = 1, f(2) = 2, f(3) = 0, f(4) = 1. Now I will show by induction that for n ≥ 2, f(2n - 1) = 0, f(2n) = 1. The base cases are clear. For f(2n - 1), the only state that can be moved to from here is that with 2n - 2 cows. By induction, f(2n - 2) = 1 > 0, so f(2n - 1) = 0. On the other hand, for 2n, removing one stone gets to a state with 2n - 1 stones, with Grundy number f(2n - 1) = 0 by induction. Using the second operation gives a Grundy number of 0 as explained above, so the smallest positive integer not achieveable is 1, so f(2n) = 1.
as k is even. Given this, it is easy to compute that f(0) = 0, f(1) = 1, f(2) = 2, f(3) = 0, f(4) = 1. Now I will show by induction that for n ≥ 2, f(2n - 1) = 0, f(2n) = 1. The base cases are clear. For f(2n - 1), the only state that can be moved to from here is that with 2n - 2 cows. By induction, f(2n - 2) = 1 > 0, so f(2n - 1) = 0. On the other hand, for 2n, removing one stone gets to a state with 2n - 1 stones, with Grundy number f(2n - 1) = 0 by induction. Using the second operation gives a Grundy number of 0 as explained above, so the smallest positive integer not achieveable is 1, so f(2n) = 1.
The case where k is odd is similar but requires more work. Let's look at the splitting operation first. This time, from a pile of size 2n we can move to k piles of size n, with Grundy number  as k is odd. So from 2n we can achieve the Grundy numbers f(2n - 1) and f(n). Using this discussion, we can easily compute the first few Grundy numbers. f(0) = 0, f(1) = 1, f(2) = 0, f(3) = 1, f(4) = 2, f(5) = 0. I'll prove that for n ≥ 2, f(2n) > 0, f(2n + 1) = 0 by induction. The base cases are clear. Now, for n ≥ 3, since a pile of size 2n + 1 can only move to a pile of size 2n, which by induction has Grundy number f(2n) > 0, f(2n + 1) = 0. Similarly, because from a pile of size 2n, you can move to a pile of size 2n - 1, which has Grundy number f(2n - 1) = 0, f(2n) > 0. Now computing the general Grundy number f(n) for any n is easy. If n ≤ 4, we have them precomputed. If n is odd and n > 4, f(n) = 0. In n is even and n ≥ 6, then f(n) is the minimal excludent of f(n - 1) = 0 and f(n / 2) (because n - 1 is odd and ≥ 5, so f(n - 1) = 0.) We can do this recursively,
as k is odd. So from 2n we can achieve the Grundy numbers f(2n - 1) and f(n). Using this discussion, we can easily compute the first few Grundy numbers. f(0) = 0, f(1) = 1, f(2) = 0, f(3) = 1, f(4) = 2, f(5) = 0. I'll prove that for n ≥ 2, f(2n) > 0, f(2n + 1) = 0 by induction. The base cases are clear. Now, for n ≥ 3, since a pile of size 2n + 1 can only move to a pile of size 2n, which by induction has Grundy number f(2n) > 0, f(2n + 1) = 0. Similarly, because from a pile of size 2n, you can move to a pile of size 2n - 1, which has Grundy number f(2n - 1) = 0, f(2n) > 0. Now computing the general Grundy number f(n) for any n is easy. If n ≤ 4, we have them precomputed. If n is odd and n > 4, f(n) = 0. In n is even and n ≥ 6, then f(n) is the minimal excludent of f(n - 1) = 0 and f(n / 2) (because n - 1 is odd and ≥ 5, so f(n - 1) = 0.) We can do this recursively,
The complexity is O(n) in the k even case and 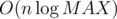 in the k odd case.
in the k odd case.
Code: http://codeforces.com/contest/603/submission/14608484
Div 1 D
Hint: It seems like this would be O(n3) because of triples of lines. Can you reduce that with some geometric observations? Think of results from Euclidean geometry relating to 4 points lying on the same circle.
First, we will prove a lemma, known as the Simson Line:
Lemma:
Given points A, B, C, P in the plane with D, E, F on lines BC, CA, and AB, respectively such that 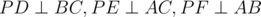 , then P lies on the circumcircle of
, then P lies on the circumcircle of 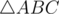 if and only if D, E, and F are collinear.
if and only if D, E, and F are collinear.
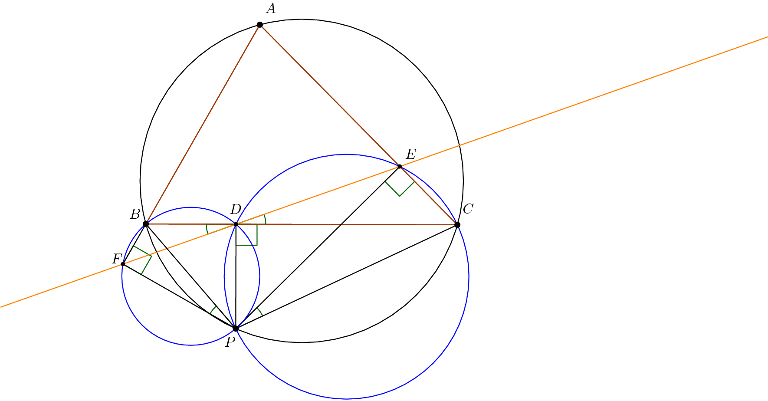
Proof:
Assume that the points are configured as shown, and other other configurations follow similarly. Recall that a quadrilateral ABCP is cyclic if and only if 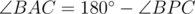 . Note that this implies that a quadrilateral with two opposite right angles is cyclic, so in particular quadrilaterals AEPF, BFPD, CDPE are cyclic. Because
. Note that this implies that a quadrilateral with two opposite right angles is cyclic, so in particular quadrilaterals AEPF, BFPD, CDPE are cyclic. Because
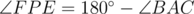
we get that ABPC is cyclic if and only if 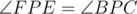 , if and only if
, if and only if 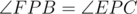 .
.
Now note that 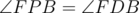 (again since BFPD is cyclic) and
(again since BFPD is cyclic) and 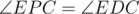 , so
, so 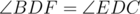 if and only if
if and only if 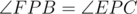 , if and only if ABPC is cyclic. Thus the lemma is proven.
, if and only if ABPC is cyclic. Thus the lemma is proven.
This lemma provides us with an efficient way to test if the circumcircle of the triangle formed by three lines in the plane passes through the origin. Specifically, for a line  , let Xi be the projection of the origin onto
, let Xi be the projection of the origin onto  . Then
. Then  form an original triangle if and only if Xi, Xj, and Xk are collinear. Thus the problem reduces to finding the number of triples i < j < k with Xi, Xj, Xk collinear. The points Xi are all distinct, except that possibly two lines may pass through the origin, so we can have up to two points Xi at the origin.
form an original triangle if and only if Xi, Xj, and Xk are collinear. Thus the problem reduces to finding the number of triples i < j < k with Xi, Xj, Xk collinear. The points Xi are all distinct, except that possibly two lines may pass through the origin, so we can have up to two points Xi at the origin.
Let us first solve the problem in the case that all points Xi are distinct. In this case, consider each i, and store for each slope how many points Xj with i < j the line Xi Xj has this slope. This storage can be done in O(1) or 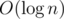 , depending on how hashing is done. Note also that we must consider a vertical line to have the valid slope
, depending on how hashing is done. Note also that we must consider a vertical line to have the valid slope  . If
. If 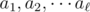 are the number of points corresponding to the distinct slopes
are the number of points corresponding to the distinct slopes 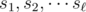 through Xi (for points Xj with i < j), then for Xi we add to the total count
through Xi (for points Xj with i < j), then for Xi we add to the total count
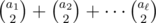
If the Xi are not distinct, we only encounter an issue in the above solutions when we consider the slope through points Xi and Xj where Xi = Xj. In this case, for any third k, Xi, Xj, and Xk are collinear. So when considering slopes from Xi in the original algorithm, we simply run the algorithm on all slopes other than the one through Xj, and simply add n - 2 to the count afterwards to account for the n - 2 points which are collinear with Xi and Xj.
Running the above, we get an algorithm that runs in O(n2) or 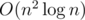 .
.
Another approach which doesn't involve the Simson line follows a similar idea: we want to find some property f(i, j) between points Xi and Xj such that the triangle formed by indices i, j, k is original if and only if f(i, j) = f(i, k). Then we can use the same argument as above to solve the problem in O(n2) or 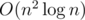 . Instead of using the slope between points i, j as the property, suppose
. Instead of using the slope between points i, j as the property, suppose  and
and  meet at some point P, and let O be the origin (again O = P is a special case). Then we let f(i, j) be the angle between
meet at some point P, and let O be the origin (again O = P is a special case). Then we let f(i, j) be the angle between  and OP. Because of the properties of cyclic quadrilaterals explained above, the triangle is original if and only if f(i, j) = f(i, k), up to defining the angle as positive or negative and modulo
and OP. Because of the properties of cyclic quadrilaterals explained above, the triangle is original if and only if f(i, j) = f(i, k), up to defining the angle as positive or negative and modulo 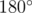 . Following this approach carefully, we can finish as before.
. Following this approach carefully, we can finish as before.
Code: http://codeforces.com/contest/603/submission/14608489
Div 1 E
Hint: What is a necessary and sufficient condition for Kevin to be able to pave paths so that each edge is incident to an odd number of them? Does this problem remind you of constructing a minimum spanning tree?
We represent this problem on a graph with pastures as vertices and paths as edges. Call a paving where each vertex is incident to an odd number of paved edges an \emph{odd paving}. We start with a lemma about such pavings:
A connected graph has an odd paving if and only if it has an even number of vertices.
For connected graphs with even numbers of vertices, we can prove this observation by considering a spanning tree of the graph. To construct an odd paving, start from the leaves of the tree and greedily pave edges so that each vertex but the root is incident to an odd number of paved edges. Now consider the graph consisting only of paved edges. Since the sum of all vertex degrees in this graph must be even, it follows that the root is also incident to an odd number of paved edges, so the paving is odd.
Now we prove that no odd paving exists in the case of an odd number of vertices. Suppose for the sake of contradiction that one existed. Then the sum of the vertex degrees in the graph consisting only of paved edges would be odd, which is impossible. Thus no odd paving exists for graphs with odd numbers of vertices.
Note that this observation turns the degree condition into a condition on the parity of connected component sizes. We finish the problem using this equivalent condition.
Suppose we only want to solve this problem once, after all m edges are added. Then we can use Kruskal's algorithm to build a minimum spanning forest by adding edges in order of increasing length. We stop once each tree in the forest contains an even number of vertices, since the graph now satisfies the conditions of the lemma. If there are still odd-sized components by the time we add all the edges, then no odd paving exists. This algorithm, however, runs in  per query, which is too slow if we want to answer after adding each edge.
per query, which is too slow if we want to answer after adding each edge.
To speed things up, we maintain the ending position of our version of Kruskal's as we add edges online. We do this using a data structure called a link-cut tree. This data structure allows us to add and delete edges from a forest while handling path and connectivity queries. All of these operations take only 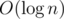 time per operation. (A path query asks for something like maximum-weight edge on the path between u and v; a connectivity query asks if u and v are connected.)
time per operation. (A path query asks for something like maximum-weight edge on the path between u and v; a connectivity query asks if u and v are connected.)
First, let's look at how we can solve the online minimum spanning tree problem with a link-cut tree. We augment our data structure to support finding the maximum-weight edge on the path between vertices u and v in 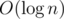 . Adding an edge then works as follows: If u and v are not connected, connect u and v; otherwise, if the new edge is cheaper, delete the maximum-weight edge on the path between u and v and add the new edge. To make implementation easier, we can represent edges as vertices in the link-cut tree. For example, if u and v are connected, in the link-cut tree they would be connected as u--e--v, where e is a vertex representing edge u--v.
. Adding an edge then works as follows: If u and v are not connected, connect u and v; otherwise, if the new edge is cheaper, delete the maximum-weight edge on the path between u and v and add the new edge. To make implementation easier, we can represent edges as vertices in the link-cut tree. For example, if u and v are connected, in the link-cut tree they would be connected as u--e--v, where e is a vertex representing edge u--v.
We solve our original problem with a similar idea. Note that the end state of our variation on Kruskal's is a minimum spanning forest after adding k edges. (We no longer care about the edges that are longer than the longest of these k edges, since the answer is monotonically decreasing---more edges never hurt.) So when we add another edge to the forest, we can use the online minimum spanning tree idea to get the minimum spanning forest that uses the old cheapest k edges and our new edge. Note that inserting the edge never increases the number of odd components: even linked to even is even, even linked to odd is odd, odd linked to odd is even.
Now, pretend that we got this arrangement by running Kruskal's algorithm, adding the edges one-by-one. We can "roll back" the steps of the algorithm by deleting the longest edge until deleting another edge would give us an odd-sized component. (If we started with an odd-sized component, we don't delete anything.) This gives us an ending position for our Kruskal-like algorithm that uses a minimal number of edges so that all components have even size---we're ready to add another edge. ("But wait a minute!" you may say. "What if edges have the same weight?" In this case, if we can't remove one of possibly many longest edges, then we can't lower our answer anyway, so we stop.)
Note that all of this takes amortized 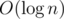 time per edge. The path queries and the insertion of the new edge involve a constant number of link-cut tree operations. To know which edge to delete, the set of edges currently in the forest can be stored easily in an STL set sorted by length. When adding an edge, we also pay for the cost of deleting that edge, so the "rolling back" phase gets accounted for. Therefore, this algorithm runs in
time per edge. The path queries and the insertion of the new edge involve a constant number of link-cut tree operations. To know which edge to delete, the set of edges currently in the forest can be stored easily in an STL set sorted by length. When adding an edge, we also pay for the cost of deleting that edge, so the "rolling back" phase gets accounted for. Therefore, this algorithm runs in 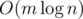 .
.
You may have noticed that executing this algorithm involves checking the size of a connected component in the link-cut tree. This is a detail that needs to be resolved carefully, since link-cut trees usually only handle path operations, not operations that involve subtrees. Here, we stop treating link-cut trees as a black box. (If you aren't familiar with the data structure, you should read about it at https://courses.csail.mit.edu/6.851/spring12/scribe/L19.pdf ) At each vertex, we track the size of its virtual subtree, as well as the sum of the real subtree sizes of its non-preferred children. We can update these values while linking and exposing (a.k.a. accessing), allowing us to perform root-change operations while keeping real subtree sizes. To get the size of a component, we just query for the real subtree size of the root.
Since the implementation of this algorithm can be rather challenging, here is a link to a documented version of my code:










Auto comment: topic has been updated by pi37 (previous revision, new revision, compare).
Whoah, Simson's line in D, nice :).
I used better known condition on whether 4 points ABCD lie on a circle: . Fix one line l and consider other line k and look at angle formed by k and line connecting origin and
. Fix one line l and consider other line k and look at angle formed by k and line connecting origin and  . Then count pairs of equal angles among angles formed by choosing all possible k's. However one should be very careful to consider proper angles (directed ones). So I needed to check whether some angles are equal. However on doubles it can be dangerous. Firstly I got ε = 10 - 9 in my solution, but my assert failed on 10th test. So I lowered it to 10 - 6, but then it failed on 3rd test! So I tried to do it on ints, but it occured that I needed integers of size up to 1032, so I abandoned that approach. As my last hopeless guess, I changed ε to 10 - 12 and it finally passed pretests and then systests :)! Estimating needed precision under pressure is not a very pleasant task :P.
. Then count pairs of equal angles among angles formed by choosing all possible k's. However one should be very careful to consider proper angles (directed ones). So I needed to check whether some angles are equal. However on doubles it can be dangerous. Firstly I got ε = 10 - 9 in my solution, but my assert failed on 10th test. So I lowered it to 10 - 6, but then it failed on 3rd test! So I tried to do it on ints, but it occured that I needed integers of size up to 1032, so I abandoned that approach. As my last hopeless guess, I changed ε to 10 - 12 and it finally passed pretests and then systests :)! Estimating needed precision under pressure is not a very pleasant task :P.
Btw when I've read statement my immediate idea was to use inversion (many circle passing through one point), I was disappointed when I discovered that this is not bringing anything good :P.
Yeah, unfortunately inversion is a bit hard to make work when you have so many lines already, because they all map to circles through the same point, which is what you're trying to get rid of :P
If you really want to solve it with inversion (ignoring lines passing through the origin, which can be dealt with separately) you get that the lines map to n circles C1, C2, ... Cn with centers O1, O2, ... On. Then i, j, k are the indices corresponding to an original triangle iff Oi, Oj, Ok, and the origin is concyclic-this is of course just the inverted version of the Simson line, but it can also be proven directly with angle chasing. So if the origin is O, we can fix each Oi and cycle through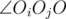 like the other solution, but this one is definitely harder :)
like the other solution, but this one is definitely harder :)
Yes, I solved it in this way. I think this one is quite complicated and time-consuming.
I was using prefix reversal twice to construct a dp but could not pass it :(...was Div2c possible with a dp solution ??
Yes, you can check my submission
http://codeforces.com/contest/604/submission/14593396
I did it with an awful DP. I don't know how to link submissions, but I kept track of 3 variables: i (the length of the prefix begin considered), j (0 or 1, the last character in the longest alternating sequence), and k, where k=0 means no flips, k=1 means inside a flip, and k=2 means the flip is done.
The recurrence isn't interesting, but it passed system tests!
Yes. I did it using dp. A position can be in one of three subsequences(till p — 1 where p is the first position that get changed, from p to q which is the last position changed, and from q + 1 to the end). You keep dp[i][j][k] = max length of a alternating subsequence formed by numbers on positions till i, the last value being j and i being in group k. You can check my source for more details
Yes. This my solution
Just feel that freaking pain... 14601989 14603923
Btw, OEIS -> 4,6,16,20,24,28,36 -> google{Sprague-Grundy sequence G(i-Mark({1}, {2}))} is ugliest way to solve the problem. Why you ever make problems that can be solved in such way?
Simson's line in D is a bad solution to be the official one. I mean, the problem after you use that is trivial, so then the whole problem becomes "do you know this obscure theorem?", and that's not really what we're going for here...
I posted this one because it was the first I thought of, and an interesting geometric way to do it (hopefully people can learn some geometry from this!)
But I agree with you that this shouldn't be the only one, so I'll post a different solution too.
I was div2 this contest :( . But I read D and it was preety cool and Swistakk's solution seems ok (and I guess that you can prove somehow the equivalence). And Simson's line is not that obscure. In my opinion, it's really nice
As a mathematician, I usually think 'this is trivial if you know the right data structure', like the link-cut tree in E, although that one still isn't trivial, even if you know link-cut trees. Mathematical problems are a nice alternation to those. Also, you might be able to come up with the required theorems/lemma's yourself, if you don't yet know them.
The complexity of Div 2 B is actually
O(n - k), and notO(n log n)as the input is already sortedFor Div 2 B, sorting is NOT needed because it is guaranteed in the problem statement that the sizes of the cowbells are sorted in non-decreasing order!! Therefore, the overall time complexity should be O(n).
Guys, about div 2 B, a different question
"Given weights s1, s2, ..., sn" and size of each box is M, what is the minimum number of boxes needed such that all weights are inside some box and each box can't hold more than 2 weights"?
Looks like the greedy algorithm of maintaining two markers left and right and pairing leftmost (current smallest) and rightmost(current largest) also works here.
Can anyone provide a proof? I attempted a wrong greedy approach which was just use weights while sum <= M, but of course this will fail if weights = 1, 1, 2, 2 and M = 3. My approach will do {1, 1}, {2}, {2}, whereas {2, 1}, {2, 1} is optimal using only two boxes.
It's the problem A (data packing) from here
https://code.google.com/codejam/contest/3014486/dashboard
I really likes the idea of HINTS in the beginning of each problem explanation :), helps a lot when we get stuck but we don't want to know the solution right away :) ..
Hopes it will continue :)
Auto comment: topic has been updated by pi37 (previous revision, new revision, compare).
Can somebody explain the solution for div2-C? any particular observations or some kind of formal proof would help. ty :D in advance.
Yes, of course :)
http://codeforces.com/contest/604/submission/14609888
The main idea is to compress the string, information was stored in vector bin. So bin.first stands for 0 or 1, and bin.second stands for quantity of corresponding digit. At first, let's denote len = bin.size() is the length of alternative sub in the given string. Then we do like this: Let's denote a = quantity of values such that their 'second' are >= 2; and b = quantity of values such that their 'second' are > 2; If b > 0 or a >= 2 then the answer will be len+2; else, the answer will be len + a;
I think in the end of Div.1 B tutorial, you should write that "our answer is p raised to the the number of connected components in the graph, not included vertex 0".
Why gcc and g++ make different output under same code??
(AC)gcc submission : http://codeforces.com/contest/604/submission/14612151
(WA)g++ submission : http://codeforces.com/contest/604/submission/14612157
It's because of the floating point.
ans must have been something like 4.999999 and it became truncated.
14612452
Thanks for this contest and the editorial!
The link for Link-Cut Trees contained an extra '.'
Plz fix this.
I solved Div 2 C/Div 1 A using dynamic programming. I feel my solution is easier to think about, so I post my explanation of the solution here.
HINT: Observe that if the single inversion condition was not given, the problem can quite easily be done in O(n) using DP state prev, index where prev = {0, 1}. The transition is O(1). Now we just have to account for the inversions.
To account for the inversions, using condition that only exactly 1 substring may be inverted, we can define each part of the sequence to be either present before the inversion, in the inversion, or after the inversion. Let us let this be denoted by another variable in the DP state named status = {0, 1, 2} such that 0 denotes that the index is not a part of the inversion and instead precedes it, 1 that it is a part of the inversion, and 2 that the it follows the inversion.
The next important observation is that when we transition between states such that status changes, we do not need to do anything other than passing the opposite of the prev value. This is because the inversion length remains same even without any other change, and the work of inverting, is essentially same as inverting the prev element. This might be a little unclear, think about it deeply to understand fully.
Now DP may be implemented in using O(n) time, with 6*n space. The state is DP(index, prev, status). The transition takes O(1) time and is somewhat trivial and left as an exercise to the reader.
Code: 14616518
I liked this dp solution more than the one mentioned in the editorial. Code : 14631653
Have you tried clicking on the code in the editorial? I'm fairly sure that your code is not more compact that the one linked in the editorial...
here
UPD: The above poster initially said that his code was more compact than our solution, but he now deleted the comment.
Lol ! My bad. Time to edit.
Brilliant DP, you save my brain
Hi everyone,
Please can someone explain me the solution for Div2 D. I could understand till f( ((k^i)*n) % p ) =( (k^i) * f(n) ) % p. But after that I could not understand how we have (p-1)/m choices for each value of n. Please help.
Try drawing a graph on the numbers 1, 2, ..., p - 1 and connect x and See what happens. Do this for k = 3, p = 11 or something.
See what happens. Do this for k = 3, p = 11 or something.
Why f(2) = 2 in div2 E ?I think it almost the whole day but still can't understand...
In the case where k is even, look at a pile of size 2. It can transition to two states: 1 pile of size 1, or two piles of size 1.
In 1 pile of size 1, the Grundy number is f(1) = 1. In the case where you have two piles of size 1, the Grundy number is So from a pile of size 2, you can reach states with Grundy numbers 0, 1. So f(2) = 2 by the definition of minimal excludant.
So from a pile of size 2, you can reach states with Grundy numbers 0, 1. So f(2) = 2 by the definition of minimal excludant.
Thanks a lot! I get it:).How ever I have classes all day . So I only have time for coding in midnight. What a pity(>﹏<)
can anyone please explain me div2c/div1a problem i dont get it ..:(
First we can only increas at most 2 elements in the initial string.Because you only can inverse a substring. You can find only the end point have posibility to increase ans if and only if they are same to their neighbor.(left end point s[i]equals s[i-1] and right s[r] equals s[r+1]). So we only need to find the string 11 or 00 in the most left position and right position . If there are 2 , then increase ans 2 ; increase ans 1 if there are 1. and 0 for none :)
Verdict is WA on TC 2 but my code works fine on my PC and its giving correct answer for TC2. I crosschecked it on even different online IDEs and its still correct. Don't know whats wrong with CF. Can anyone check this one? http://codeforces.com/contest/604/submission/27927286 Submission id : 27927286
Declare the arrays globally. I tried and it gave correct answer on both test 1 and test 2.
Just in case if anyone wants a recursive DP solution of div2C : 76280888
Iterative version for div 2 C/div 1 A.....here.