Now that we know how to sieve properly, let's look at hacks to the Eratosthenes sieve to get some other interesting sieves.
Introducing a problem
Let's say we want to count the number of divisors of a number. One way is to check all numbers up to √n and check if n divides that number. The other way is to get its prime factorization and get the product of (exponent + 1) through combinatorics. Either method is O(√n) on average, thus O(n√n) if done for all numbers up to n.
But what if a problem asks us to print the number of divisors of all numbers from 1 to 10^7 under 3 seconds? An O(n√n) algorithm will be too slow! When I tried counting divisors using the square root method, it ran for about 61 seconds on my computer. That definitely won't run in time.
Fortunately, we can tweak the Eratosthenes sieve to count the number of divisors more efficiently and elegantly. And you will see that this technique works not only for number of divisors, but also for generating sum of divisors, totient function, biggest prime divisor, basically all functions that have to do with divisors!
Divisor Sieve O(n log n)
int divisors[n + 1];
for (int i = 1; i <= n; ++i)
for (int j = i; j <= n; j += i)
++divisors[j];
OK, so what's up with this rather short code? This short code generates the number of divisors of all numbers less than or equal to n. Oh wow, just solved our problem! But wait, aren't we too rushed? Does this code even work? And how does it even work in the first place? How did we come up with O(n log n)? Don't worry, we'll answer those questions one by one.
Correctness
We want to count the number of divisors of a number. On another perspective, we can instead start from the divisor then increment the count of all its multiples. Do that for all divisors, we now have all divisor counts of all numbers up to n.Hurray.
Complexity
Now that we have proved that the algorithm is correct, how are we sure that the complexity is O(n log n) when it looks like O(n^2)? The answer is because we are summing a harmonic series. The inner loop runs ⌊n / i⌋ iterations, therefore, the total number of iterations is:
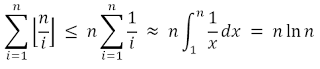
If you know calculus, the count just approximates to the Riemann sum of the harmonic series, which we can integrate to get n log n. Mathemagic at its finest.
In general, O(n log n) for n = 10^7 runs for approximately 1.700s on a normal computer, and even faster on online judges that do cloud computing. This already solves our problem, and heck, with really short code!
Sum of Divisors Sieve O(n log n)
int sumdiv[n + 1];
for (int i = 1; i <= n; ++i)
for (int j = i; j <= n; j += i)
sumdiv[j] += i;
We can also use this technique to get sum of divisors. Just increment by the divisor instead of just incrementing by 1.
Euler Totient Sieve O(n log log n)
int totient[n + 1];
for (int i = 1; i <= n; ++i) totient[i] = i;
for (int i = 2; i <= n; ++i)
if (totient[i] == i)
for (int j = i; j <= n; j += i)
totient[j] -= totient[j] / i;
This technique could also generate the Euler totient function, where totient[a] is the number of positive integers less than a that is relatively prime to a. It's O(n log log n) because it does the inner loop only if the number is prime (see prime harmonic series).
You might ask why it's totient[j] -= totient[j] / i. This is due to the nature of the Euler totient function, which needs some background of number theory to prove. This wonderful blog entry by PraveenDhinwa provides a good explanation of it if you want the extensive proof.
Biggest Prime Divisor Sieve O(n log log n)
int big[n + 1] = {1, 1};
for (int i = 1; i <= n; ++i)
if (big[i] == 1)
for (int j = i; j <= n; j += i)
big[j] = i;
We can tabulate the biggest prime divisor per number. This is useful for pruned prime checking (when big[p] == p) and easier prime factorization. You don't need to iterate through all the primes to prime factorize anymore, you just need to a single while loop, something like while (n > 1) { factors.push_back(big[n]); n /= big[n]; }.
There are many more extensions of the wonderful Eratosthenes sieve. If you know some interesting ones, please let me know as well so I can add it (and credit you) in this blog.
Disclaimer: I was the one who named the "sieves" so they're not official names or anything. Moreover, they're not technically sieves anymore (sieves are filters, but the functions above are number generators), but I thought the sieve label was cool so I put it, if you don't mind.











(https://www.codechef.com/problems/SMPLSUM) This is a really good problem where you can use these concepts
Given L and R, how to find number of divisors of all the numbers between L and R ? Given 1<=L<=R<=(10^12) and (L-R)<=(10^5)
What is the source of the problem?
Lol
He is trying to ask from a live contest Here
I dont know why people ask like this during the contests. Do they read rules of the contest and still ask?
PS:This is not first time I am seeing such question.
Deleted Comment
P.S Sent and deleted after teja349's comment :)
I am very sorry for it friends. Will make sure I don't do anything like this in future. I am a budding programmer, struggling my way through the competitive world and learning stuffs. Thank you teja349 and Batman for pointing me out. Awesome community, I will make sure I do my best in future. Cheers..
All the Best!!!
https://codeforces.com/problemset/problem/1529/D Good question to apply the concepts learned
Looking for the Mobius function precomputation using sieve...
Can someone pls provide it?