Topic : Counting Divisors of a Number
Pre Requisites : Basic Maths , 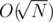 Factorisation , Primality testing
Factorisation , Primality testing
Motivation Problem :
There are T test cases. Each test case contains a number N. For each test case , output the number of factors of N.
1 < = T < = 10
1 < = N < = 1018
Note : 1 and N are also treated as factors of the number N.
Solution :
Naive Solution — 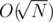 Factorisation
Factorisation
The most naive solution here is to do the 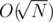 factorisation. But as we can see, it will surely receive the Time Limit Exceeded verdict. You may try to compute the prime numbers till required range and loop over them , but that too exceeds the usual limit of 108 operations. Some optimisations and heuristics may allow you to squeeze through your solution, but usually at the cost of a few TLE's.
factorisation. But as we can see, it will surely receive the Time Limit Exceeded verdict. You may try to compute the prime numbers till required range and loop over them , but that too exceeds the usual limit of 108 operations. Some optimisations and heuristics may allow you to squeeze through your solution, but usually at the cost of a few TLE's.
Supposing you fit in the above description and cannot think of anything better than the naive solution, I would like to present to you a very simple algorithm which helps you count the number of divisors in 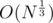 , which would be useful for this kind of questions. This algorithm only gives us the count of factors, and not the factors itself.
, which would be useful for this kind of questions. This algorithm only gives us the count of factors, and not the factors itself.
Firstly, let's do a quick recap of how we obtain the 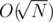 algorithm for any number N :
algorithm for any number N :
We write N as product of two numbers P and Q.
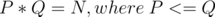
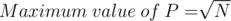
Looping over all values of P gives us the count of factors of N.
Before you move forward to the next section, it would be useful if you try to come up with an algorithm that finds the count of factors in 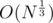 . As a hint, the way of thinking is same as that of getting to the
. As a hint, the way of thinking is same as that of getting to the 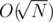 algorithm.
algorithm.
Counting factors in 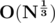
Let's start off with some maths to reduce our 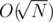 factorisation to
factorisation to 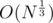 for counting factors :
for counting factors :
We write N as product of three numbers P, Q and R.
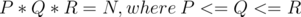
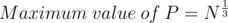
We can loop over all prime numbers in range 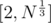 and try to reduce N to it's prime factorisation, which would help us count the number of factors of N.
and try to reduce N to it's prime factorisation, which would help us count the number of factors of N.
To know how to calculate divisors using prime factorisation, click here.
We will split our number N into two numbers X and Y such that X * Y = N. Further, X contains only prime factors in range 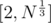 and Y deals with higher prime factors (
and Y deals with higher prime factors (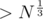 ). Thus, gcd(X , Y) = 1. Let the count of divisors of a number N be denoted by the function F(N). It is easy to prove that this function is multiplicative in nature, i.e., F(m * n) = F(m) * F(n), if gcd(M,N) = 1. So, if we can find F(X) and F(Y), we can also find F(X * Y) or F(N) which is the required quantity.
). Thus, gcd(X , Y) = 1. Let the count of divisors of a number N be denoted by the function F(N). It is easy to prove that this function is multiplicative in nature, i.e., F(m * n) = F(m) * F(n), if gcd(M,N) = 1. So, if we can find F(X) and F(Y), we can also find F(X * Y) or F(N) which is the required quantity.
For finding F(X), we use the naive trial division to prime factorise X and calculate the number of factors. Once this is done, we have Y = N / X remaining to be factorised. This may look tough, but we can see that there are only three cases which will cover all possibilities of Y :
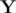 is a prime number : F(Y) = 2.
is a prime number : F(Y) = 2.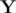 is square of a prime number : F(Y) = 3.
is square of a prime number : F(Y) = 3.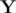 is product of two distinct prime numbers : F(Y) = 4.
is product of two distinct prime numbers : F(Y) = 4.
We have only these three cases since there can be at max two prime factors of Y. If it would have had more than two prime factors, one of them would surely have been 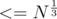 , and hence it would be included in X and not in Y.
, and hence it would be included in X and not in Y.
So once we are done with finding F(X) and F(Y), we are also done with finding F(X * Y) or F(N).
Pseudo Code :
N = input()
primes = array containing primes till 10^6
ans = 1
for all p in primes :
if p*p*p > N:
break
count = 1
while N divisible by p:
N = N/p
count = count + 1
ans = ans * count
if N is prime:
ans = ans * 2
else if N is square of a prime:
ans = ans * 3
else if N != 1:
ans = ans * 4
Checking for primality can be done quickly using Miller Rabin. Thus, the time complexity is 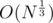 for every test case and hence we can solve our problem efficiently.
for every test case and hence we can solve our problem efficiently.
At this point, you may think that in a similar way, we can reduce this to 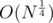 by handling some cases. I have not thought much on it, but the number of cases to be handled are high since after trial division N could be factorised into one, two or three primes. This is easy enough to code in contest environment, which is our prime objective.
by handling some cases. I have not thought much on it, but the number of cases to be handled are high since after trial division N could be factorised into one, two or three primes. This is easy enough to code in contest environment, which is our prime objective.
This trick is not quite commonly known and people tend to make bugs in handling the three cases. A problem in regionals which uses this trick directly :
You can try also this technique on problems requiring 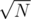 factorisation for practice purposes.
factorisation for practice purposes.
Hope you found this useful! Please suggest more problems to be added as well as any edits, if required.
Happy Coding!











Good one :) (Y)
You can't really call this "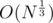 factorization" though, you only get the exponents, not the factors.
factorization" though, you only get the exponents, not the factors.
Agreed, that's why I put the title as "Counting Divisors". For the sub heading, I couldn't think of anything short and simple, so I went ahead with that. What could it be changed to?
Edit : I edited the post so that it isn't misleading anymore!
Looks good now, good work :).
No wait I missed some cases, ignore :P
What is N here?
N = 101 * 101 * 97.
Ah, I see, we don't necessarily have a prime factor less than the 4th root of the number
Auto comment: topic has been updated by himanshujaju (previous revision, new revision, compare).
To check if N is prime or not at the end of your algorithm you have to use O(sqrt(n)) algorithm...
Read up on Miller Rabin, I mentioned that explicitly in the post.
Ok...tnx...I'll read about it
You mentioned the following part --
We have only these three cases since there can be at max two prime factors of Y.If it would have had more than two prime factors, one of them would surely have been , and hence it would be included in X and not in Y.Could you please explain this part a bit in detail. I am still now sure about why there can be at max two prime factors for Y and not 3 or more.
Suppose N has 3 primes factors left after the trial division is done. So, N = p1 * p2 * p3.
Now , p1 , p2 and p3 all have to be greater than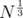 or else they would have been found in the trial division. Their product will be greater than N , which is not possible and hence we contradict what we started with.
or else they would have been found in the trial division. Their product will be greater than N , which is not possible and hence we contradict what we started with.
Try a few examples in pen and paper and read this proof again in case you still don't understand. Don't hesitate to reply for any clarifications.
What is a good way for checking whether a given number is a square?
I'm using this:
.
It checks whether n is a power of two, not a square.
Sorry guys I accept my mistake, is there a way to remove the comment
Someone please provide code for Miller-Rabin primality test. Thanks!
This provides a nice explanation as well
Explanation was good but the code was not fully correct, plz can someone provide the code.
I tried solving the problem using Miller-Rabin as you said. The thing is: when we are limited to ~ 64 bits, doing an exponentiation a^d (mod n) may give overflow. This happens because, if n is too large (like 10^18), the value of a^d will overflow before we can apply the modulus operator (applying it when it is less than n won't help). Is there any way to overcome this or do we need to work with bigger types?
I use this to avoid overflow (taken from topcoder tutorial on primality) :
2015:
`
__int128is a non-standart GCC extension. For example, Microsoft has no plans to implement it in MSVCcan u provide links to some spoj problem that uses this technique?
Unfortunately, I know only one question yet. You can use this on any question where logic for counting factors also passes. Havnt been solving on SPOJ recently, so no idea.
logic for counting factors also passes. Havnt been solving on SPOJ recently, so no idea.
The Pollard-rho algorithm can give the factorization of n in O(n1 / 4) time.
When Y consist of two prime or Y is a prime how can i check it. Thanks in Advance.
suppose Y<=10^18.
iterate over all primes from 2 to 10^6 and keep dividing Y by them meanwhile keep a count of factors.
After this step either you have found the solution or the Y left contains prime factors > 10^6 .
NOTE : now notice that Y cant have more than two prime factors at this step because factors left are already greater than 10^6 .
Am I allowed to translate it to Chinese with your name on it?
Sure! With/without name doesn't matter much :)
please can you explain why F(y) ={ 2 , 3 , 4 } in the three cases !! I understand why we have only three cases but I can't understand who we get F(y) value .. thanks in advance
Can you please share your accepted code for the above Problem.
Can someone elaborate on how we can check if Y is any of the three cases? I can't see this through!
Check if Y is a prime number by using Miller Rabin test.
If it fails, check if the sqrt of Y is prime by using the same test.
If that fails too, then the number must belong to the third case.
Did u solve the above problem Vicennial?-
upd: solved by removing the sqrt() fun
ok. suppose, we want to check nod of a prime number and this number is n>10^6; so,in your pseudo code, the number failed to go through in 1st while loop; after it comes [ if N is prime ] this condition. but we stored prime only up to 10^6. since the number can't go through while loop and the value of the number (n) cannot be changed, how I check the number is prime or not???? how it passes this [ if N is prime ] condition???
Example, if a number is 50761746622, what is it's output??
You don't use the sieve to check if the result is prime. You use Rabin-miller probabilistic primality testing to check if it is prime. Look up "Rabin-Miller" and go to wikipedia to read about it. It is a way to check with high probability that a number is prime or not.
If N is a prime number greater than 1e17 then Y=N. So, how to check whether Y is prime or Y is a square of prime or Y is product of two prime? (Initially it is not known that N is prime greater than 1e17)
Fermat's primality test
I have written the for this topic, You can check it here : http://codeforces.com/blog/entry/62105
Pollard's rho algorithm can do the factorization in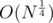 complexity
complexity
implementation any?
This one is the same as described one..
i submitted this code on this problem and i got WA do you know what the wrong ?
my code : 69619960
I know this is necroposting but we can reduce the complexity downto $$$O(N^{\frac{1}{4}})$$$ or generalized to $$$O(N^{\frac{1}{k}})$$$ (though I am not sure about the time complexity)
Let $$$N = X \times Y$$$ for $$$1 \leq X \leq N^{\frac{1}{4}} < Y \leq N$$$
Yes, it is possible, for $$$A, B, C$$$ distint primes
1) $$$Y = A$$$ is a prime $$$\rightarrow F(Y) = 2$$$
2) $$$Y = A^2$$$ is a square of prime $$$\rightarrow F(Y) = 3$$$
3) $$$Y = A^3$$$ is a cube of prime $$$\rightarrow F(Y) = 4$$$
4) $$$Y = A \times B$$$ is a squarefree semiprime $$$\rightarrow F(Y) = 2 \times 2$$$
5) $$$Y = A \times B \times C$$$ is a sphenic number $$$\rightarrow F(Y) = 2 \times 2 \times 2$$$
6) $$$Y = A^2 \times B$$$ is a cubefree product of square of a prime and a prime $$$\rightarrow F(Y) = 3 \times 2$$$
What is the complexity of the the function (anyDivisor of n) , Also what you do in it
It is $$$Õ\left(\sqrt{_\sqrt{n}^{\text{ }}}\right) = Õ\left(n^{1/4}\right)$$$ for which $$$Õ(n) = O\left(n \text{ polylog } n\right)$$$
In my implementation, you can optimize them in certain ways to optimize further for general cases. (For examples: deterministic miller rabin, $$$O(1)$$$ modulo multiplication, reduce amount of modulo operations).
I was explaining that if there is an algorithm better than pollard rho exists, let it be $$$O(f(n))$$$ then we can count divisors by making $$$N = X_1 \times X_2 \times ... \times X_k$$$, for $$$1 \leq X_1 \leq N^{1/k} \leq \frac{N}{X_1} \leq N$$$ then check for each case whether $$$X_i = X_j$$$ are the same prime or not (each yelling a different $$$F(Y)$$$ value mentioned earlier in my comment)
Ohh it is pollard rho I never have its implementation and now i have
Thanks
We don't really need to use Miller-Rabin test, because there are no Carmichael numbers with two prime factors. we can use Fermat test instead.
Why not use Pollard's rho algorithm?