A naive solution works in O(nmk). This solution stores all the start positions into an array and next iterates over all commands and shifts positions in needed directions. After every move it checks that all positions lie on the exit cell.
This solution doesn't fit into time limits.
An author's solution speed up the naive solution with using of bit masks.
All current positions of robot you should store in rectangular bit mask of size n × m. This mask should provide following operations:
1. Shift left, right, up, down.
2. Binary operations AND and OR.
3. Compare with another mask.
All these operations can be realized so that they will work in O(nm / 32) time. You can use array of 32-bit integers of size n × m / 32 or std::bitset in C++.
How to emulate process?
At first, you should create a mask base that has 1-bit for every passable cell and 0-bit otherwise.
Now you should create sevaral additional masks for all four directions: up1, up2, left1, left2, down1, down2, right1, right2. Masks with index 1 store cells that lie near wall, ans masks with index 2 store all other cells of mask base.
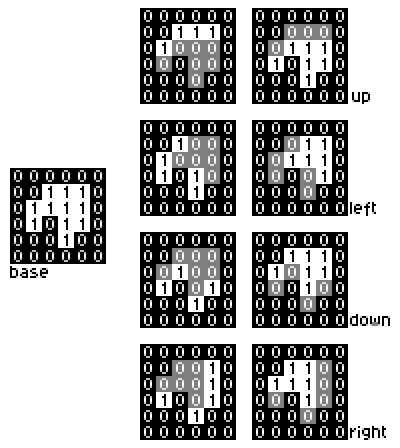
Also you should create mask E that has only one 1-bit in the exit cell.
Let all current positions of robor are given by mask T. Split T into 2 sets of positions: all ones that lie near wall (the first set) and all other ones (the second set). Now you should shift all positions in the second set and next merge two sets into one. The finish set gives new mask T. This transformation in operations with masks looks like:
T = ((T and up1) or shift_up(T and up2));
You can transform T analogically for other three directions.
Now you should iterate over all commands and do transformations. On every step you should compare T with E. As soon as they are equal, you should output number of a command after that it happened. If always T and E are unequal, you should output -1.
This solution has complexity O(nmk / 32). Author's solutions on C++ and Java without any serious optimizations work in 0,9 sec and 2,3 sec correspondingly.










