Some of you made the mistake of demanding an article on one of my favorite topics. (DP)

Note that the article might be simple for a big part of you as it is intended for the general public. .
Cutting to the chase
As a young programmer, I heard about DP from contests. Searched it on Google. Urban Dictionary gave unsatisfying results. Then I searched for Dynamic Programming on Wiki and found that:
"dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions — ideally, using a memory-based data structure"
Sounds pretty general, huh? Let's get there step by step.
Lights, camera, action
Breaking a problem into subproblems does not seem as obvious as there are many many ways to look at it. You can imagine this as a setting for some action. The setting can be really everything: a house, a string, a graph and so on. At each moment some actions happens. If the actions are limited we can have an overview of them and represent them somehow.
We call the representation of a setting at some moment a state. For short you can regard the whole thing as a film: more frames one after the other that are bound. The frames are the states and we need to figure out what to store and how to get from start to end. In some sense you are a director and make a film in each problem. (Of course, you have budget and deadline, but we'll get there latter) Now let's put on our first film:
An Unexpected Journey
The "world" will be New Zealand. But to be fair, we'll call it just "The Shire" and we'll represent it as 2D matrix:
+--+--+--+--+
| | | | |
+--+--+--+--+
| | | | |
+--+--+--+--+
| | | | |
+--+--+--+--+
| | | | |
+--+--+--+--+
Now let's add some inhabitants. Call them Bilbo and Gollum. Now they are placed in this world:
+--+--+--+--+
| G| | | |
+--+--+--+--+
| | |B | |
+--+--+--+--+
| | | | |
+--+--+--+--+
| | | | |
+--+--+--+--+
So far so good. Now we need a sensible representation of those two and other possible inhabitants. In this scenario the coordinates would be fair enough. Therefore we have B(2, 3) and G(1, 1).
1 2 3 4
+--+--+--+--+
1 | G| | | |
+--+--+--+--+
2 | | |B | |
+--+--+--+--+
3 | | | | |
+--+--+--+--+
4 | | | | |
+--+--+--+--+
Our world seems somehow still. So let's add some action. So Gandalf goes to Bilbo and says: "I'm looking for someone to share in an adventure." and the hobbit starts moving in 4 possible directions: N, S, E, W.
1 2 3 4 1 2 3 4 1 2 3 4
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
1 | G| | | | 1 | G| | | | 1 | G| | | |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
2 | | |B | | 2 | | | | | 2 | | |B | |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
3 | | | | | 3 | | |B | | 3 | | | | |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
4 | | | | | 4 | | | | | 4 | | | | |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
1 2 3 4 1 2 3 4 1 2 3 4
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
1 | G| | | | 1 | G| | | | 1 | G| | | |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
2 | | | |B | 2 | | | | | 2 | | | | |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
3 | | | | | 3 | | | |B | 3 | | | | |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
4 | | | | | 4 | | | | | 4 | | | |B |
+--+--+--+--+ +--+--+--+--+ +--+--+--+--+
Now that we added frames Bilbo seems to be moving around. Now we have to add time, so a possible representation of Bilbo's journey would be:
Place[t] = (x, y)
Therefore, Bilbo is at coordinates (x, y) at time stamp t. Now, having the representation of a single frame we have to bind around the frames. We know Bilbo's directions in order "SNESS" and his initial state (2, 3). Now we only need to find Bilbo's position at each step. We know that at each step he only moves once according to the direction indicated, so the new position can be found just by looking at the last position and the direction. Finding how to jump from a state to the other is called recurrence relation (all transitions look the same in some way, they recur).
Place[t+1] = | current_direction == 'N' = (Place[t].x - 1, Place[t].y)
| current_direction == 'S' = (Place[t].x + 1, Place[t].y)
| current_direction == 'W' = (Place[t].x, Place[t].y - 1)
| current_direction == 'E' = (Place[t].x, Place[t].y + 1)
My precious
You did not forgot Gollum, right? Not being as smart as Bilbo, he can only move down and right. And he starts from cell (1, 1) and wants to go to (4, 4). Suppose we want to find out how many ways are there for him to get there.
We can describe Gollums state as (x, y, t) and we want to know in how many ways he arrived in this state. Therefore our transitions would look like (x, y, t) -> (x2, y2, t2), more specifically (x, y, t) -> (x + 1, y, t + 1) and (x, y, t) -> (x, y + 1, t + 1).
Observe there is time dimension as he travels just down and right, therefore is a single moment in time he can arrive in a certain cell. This seem trivial, but in fact is very important. Often we care just about certain parameters as other can be deduced from the context. In this context time is t = x + y - 2. So our transitions can actually discard t.
The only thing we need to do is to store the data in each state and to transfer it into the new state. How we transfer data? The number of possibilities of arriving in a cell (x, y) are limited to arriving from (x - 1, y) and (x, y - 1). Therefore our recurrence would look like:
waysToArrive[x][y] = waysToArrive[x-1][y] + waysToArrive[x][y-1]
So, that's how things work so far... Now, let's try to discuss some general approaches...
Why is DP hard?
People often find DP hard because they do not look for certain things that appear in a lot of classic dynamic programming. Also, they often try to find a magical unicorn in the front yard. Sorry, they look for a recurrence before clearly establishing their states and data to be stored. There are three thing that I think are very important.
State reduction
The first thing that appears in a lot of problems is the concept of state reduction. We always need to look for unnecessary information we store in a state or even in the data we store. For example, an obvious state reduction is the t = x + y - 2 one.
To put more empathy on this, let's take a better example. You have an array of ints and querys that ask for sum on interval (l, r).
The obvious solution is to define:
sm[l][r] = sum on interval (l, r) where l <= r
sm[l][r] = | l == r = el[l]
| otherwise = sm[l][r-1] + el[r]
Now the observation that you have to make is that: sm[l][r] = sm[1][r] - sm[1][l-1]. We can see that in the right side is always an 1 in the first argument, so it is not useful any more. Therefore just define sm2[l] = sum on interval (1, l) and you're done.
State expansion
Let's say now we want to track Bilbo's ways of moving from point A to B. Now we have 4 directions. Even if you would be tempted to use just (x, y) as a state, now the time stamp t is necessary.
In some problems you can't find the recurrence just because you just do not have enough data.
Suppose you have an array and you want to find sum on many intervals. Let's take the obvious solution and
Frame smart
Each "frame" transition has it's own way of change. For example a graph BFS traversal is like a wave propagation. You have to look for those specific features that describe are specific to your particular problem. The BFS case transition if much simple to model using a queue as an aid structure.
1, 2, 3... GO!
I did not mentioned the general, well-known trick. Just start the problem. If you found a solution(it does not matter how bad it is, or if it is only a particular case), you have material to reduce, expand and frame smart on.
Let's say we have the interval sum problem but in 2D. A great start is to do it slow. Or, even better, try it in 1D. You'll get some insight and have an idea how to start.
For 1D, to find sm[l][r](red) we extract sm[1][l-1](green) from sm[1][r](yellow).

The same principle can be applied for 2D as follows:
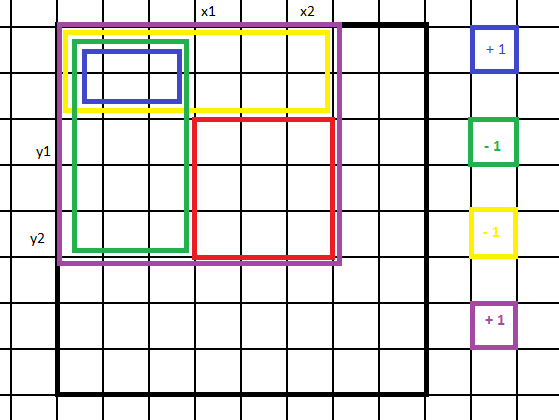
Conclusion
In my opinion all problems have some DP view, so you just have to search for it. The more experience you have the more patterns you see.
The crucial thing is to regard DP not just as a own standing topic, but just as a pattern that occurs in more problems, so you can use it in your own advantage.
PS
Thank you for reading and please state your opinion on my tutorial. (or, more specifically, on my writing style and how useful you find the material presented) Any suggestions for next tutorial are welcome.
You can find my previous article here.
Hope you enjoyed!











was expecting this from your previous post s comments .........
the next topic iam expecting from you is HLD ..... :p
Is on the queue, but I have something little different before in plan.
Amazing, thank you so much
Dude your tutorials are awesome