625A - Guest From the Past
Idea author: collaboration, preparation: feldsherov.
If we have at least b money then cost of one glass bottle is b - c. This means that if a ≤ b - c then we don't need to buy glass bottles, only plastic ones, and the answer will be  . Otherwise we need to buy glass bottles while we can. So, if we have at least b money, then we will buy
. Otherwise we need to buy glass bottles while we can. So, if we have at least b money, then we will buy 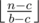 glass bottles and then spend rest of the money on plastic ones. This is simple O(1) solution.
glass bottles and then spend rest of the money on plastic ones. This is simple O(1) solution.
625B - War of the Corporations
Idea author: gustokashin, preparation: thefacetakt.
Lets find leftmost occurrence of the second word in the first one. We need to add # to remove this occurrence, so where we would like to put it? Instead of the last symbol of this occurrence to remove as many others as we can. After that we will continue this operation after the new # symbol. Simplest implementation of this idea works in O(|S|·|T|), but with the power of string algorithms (for example, Knuth–Morris–Pratt algorithm) we can do it in O(|S| + |T|) time.
Hint/Bug/Feature: in Python language there is already function that does exactly what we need:
print(input().count(input()))
625C - K-special Tables
Idea author: Elena Andreeva, preparation: wilwell.
Lets fill our table row by row greedily. We want to have maximal possible number on k-th place in the first row. After it we need at least n - k numbers greater than ours, so its maximum value is n2 - (n - k). If we select it then we are fixing all numbers after column k in the first row from n2 - (n - k) to n2. On the first k - 1 lets put smallest possible numbers 1, 2, ... , k - 1. If we do the same thing in the second row then in the beginning it will have numbers from k to 2(k - 1), and from k-th position maximum possible values from n2 - (n - k) - (n - k + 1) to n2 - (n - k + 1). And so on we will fill all rows. With careful implementation we don't need to store whole matrix and we need only O(1) memory. Our algorithm works in O(n2) time.
625D - Finals in arithmetic
Idea author: Sender, preparation: Sender.
Lets say that input has length of n digits, then size of answer can be n if we didn't carry 1 to the left out of addition, and n - 1 otherwise. Lets fix length m of our answer and denote i-th number in the representation as ai. Then we know 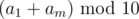 from the rightmost digit of the sum. Lets figure out what does
from the rightmost digit of the sum. Lets figure out what does 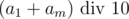 equals to. If the remainder is 9, it means that
equals to. If the remainder is 9, it means that 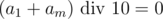 , because we can't get 19 out of the sum of two digits. Otherwise the result is defined uniquely by the fact that there was carrying 1 in the leftmost digit of the result or not. So after this we know a1 + am. It doesn't matter how we divide sum by two digits, because the result will be the same. After this we can uniquely identify the fact of carrying after the first digit of the result and before the last digit. Repeating this m / 2 times we will get candidate for the answer. In the end we will have O(n) solution.
, because we can't get 19 out of the sum of two digits. Otherwise the result is defined uniquely by the fact that there was carrying 1 in the leftmost digit of the result or not. So after this we know a1 + am. It doesn't matter how we divide sum by two digits, because the result will be the same. After this we can uniquely identify the fact of carrying after the first digit of the result and before the last digit. Repeating this m / 2 times we will get candidate for the answer. In the end we will have O(n) solution.
If you've missed the fact that every step is uniquely defined, then you could've wrote basically the same solution, but with dynamic programming.
625E - Frog Fights
Idea author: Elena Andreeva, preparation: iskhakovt.
We want to efficiently simulate the process from the problem statement. Lets have a data structure with times of key events that could've happened during simulation (some frog removed other frog from the board). Lets remove earliest event from our data structure and apply it to the board, make a critical jump. After that the speed of the first frog will decrease and we will be forced to recount times of collision of this frog this its 2 neighbors. This data structure could be set from C++, TreeSet from Java or self-written Segment Tree. To quickly find out who are we gonna remove from the board after the jump lets store double-linked list of all frogs sorted by their positions. Technical part is to calculate time of the collision, but it can be easily done with the simple notion of linear movement of two points on a line. There could be at max n - 1 collisions, so whole solution will be  .
.










Thanks for nice editorial!
Can anybody help explain or give intuition as to why is the formula for A that? The n-c bit.
Lets say that we reserve c coins for later, then we can spend b - c coins plus reserve on the bottle and get the reserve back, so the reserve stays untouched. And after we bought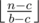 glass bottles we can't buy another one, because n1 - c < b - c, which is the same as n1 < b.
glass bottles we can't buy another one, because n1 - c < b - c, which is the same as n1 < b.
Also, some people used
floor( (n-b)/(b-c) ) + 1. Is it the same as that formula? It does give AC on the system tests.
http://codeforces.com/contest/625/submission/15870223
Its the same formula and will give AC if you add the condition if(b<=n)
Yeah, I was a little slow. Thanks for appreciating slow learners with negative contribution Codeforces community!
Also, thanks for clarifying mate! :)
"Lets say that we reserve c coins for later, then we can spend b - c coins plus reserve on the bottle and get the reserve back, so the reserve stays untouched."
I am sorry, but I don't understand that sentence. I've reread it several times and still don't see how it comes that the numerator is n - c. Could you, please, give a little bit more detail?
what is the dynamic programming solution for D ?
dp[how many digits from both sides we are already passed][is there a carry to the left][is there a carry from the the right], and to move to the next position we will iterate over the sum of the left digit and the right digit, which we are passing now.
can you please illustrate how are we getting ans for 867 -> ans(285) and 165 -> ans( 87 ) and 111 (ans->0) using above mentioned tutorial for problem D
Problem A soln — >
if (b-c) <= a
equation reduces to
here is the code 15886431
How did you add 1 to
RHSfromk > (n - b) / (b - c)to make them equal?you have made a mistake , it should be
and i have added one to make it strictly greater
thanks, got it!
np!
Lets have a data structure with times of key events that could've happened during simulation (some frog removed other frog from the board)
How do I calculate this list of events in less than O(N*N) ? I am really confused and I think that to calculate all different collisions I would need to calculate collision time of each frog to each other frog. How can I handle it?
You need to calculate the events only for the neighbors of each frog, It can be done with a bidirectional linked list.
Notice, that the order of the frogs doesn't change during the game, some of them are just knocked out.
dammit. I almost had A . Same logic. Only blunder I made was forgetting b can be greater than N :/
Same here. :(
I'd like to thank the hacker of my Problem A for rescuing 300+ points. It's never a good idea to get hacked by system tests.
+1. I wish I was hacked instead of FST.
My solution for Problem D with dp is this -
Let the answer be a 5 digit number then it is written like this.
a4 * 10^4 + a3 * 10^3 + a2 * 10^2 + a1 * 10^1 + a0 * 10^0
Then its reverse is —
a0 * 10^4 + a1 * 10^3 + a2 * 10^2 + a3 * 10^1 + a4 * 10^0
The sum of the 2 numbers is —
(a0 + a4) * (10^0 + 10^4) + (a1 + a3) * (10^1 + 10^3) + (a2 + a2) * (10^2 + 10^2)
This means that a0 and a4 contributes to the 0th place and 4th place of the number to be made, where if a0 + a4 >= 10 then it would give a carry over to the 1st and 5th place.
Similiarly, a1 and a3 contributes to the 1st and 3rd place of the number to made, where if a1 + a3 >= 10 then it would give a carry over to the 2nd and 4th place.
Also we know that at max the carry over will be of at max 1 only.
Intuition -> 99999...9999 + 99999...9999 (Here also only a carry over of at max 1 takes place)
Now we have also established relationship between (a0, a4) and (a1, a3), ie.
If((a0 + a4) % 10 == 4th place) then a1 + a3 < 10, this is because the carry over given by a1 + a3, wouldve disturbed the equality on the 4th place.
Otherwise, If((a0 + a4 + 1) % 10 == 4th place) then a1 + a3 >= 10, this is because the carry over given by a1 + a3 is necessary for the equality on the 4th place.
Also,
If(a0 + a4 >= 10) then (a1, a3) gets a carry over on the 1st place, but NOT on the 3rd place.
Else if(a0 + a4 < 10) then (a1, a3) doesn't get a carry over on the 1st place.
Now our dp[i][greater_than_equal_to_ten][carry_over_till_here] = true, If for any (a, b), 0 <= a, b <= 9, we can make a number from i to len-i-1, where the carry over on the left place given by previous state is (carry_over_till_here) and the number (a, b) is restricted to either be >= 10 or < 10 so as to support the previous state's right place.
Net complexity — (N * 2 * 2) (number of dp states) * (10 * 10) time taken to solve a dp ==> O(N*400)
For clear understanding or to handle the corner case where i == n/2, refer my code ==> 15894317
If u could add some comments to your soln , it would be grt
Here. 15898045
In prob D how to determine if there was carry or not? I didnt understand the line "Let us figure out what does \sout.....equals to"
can anybody explain editorial for probelm E. what is mean of "times of key events that could've happened during simulation"
In this case the key event will be elimination of a frog. see the line reads "(some frog removed other frog from the board)". So here we store time of elimination of frog with other details.
maxA->number of plastic bottles maxB->number of glass bottles
otherwise: suppose we have n=14 rubles , b=8 rubles for each glass bottle at each c from 1 to 7
we can see that at c=1, valid n are 14 at c=2, valid n are 14 at c=3, valid n are 14,9 at c=4, valid n are 14,10 at c=5, valid n are 14,11,8 at c=6, valid n are 14,12,10,8 at c=7, valid n are 14,13,12,11,10,9,8
if we want to know number of valid values of n so we conclusion this equation : (n=14, b=8) length of numbers = n-b+1 then divide it over b-c we need ciel value so we add denominator-1 so equation will be (n-b+1 + b-c-1) / (b-c) save this value at maxB->number of glass bottles
reminder rubles we can buy plastic bottles with it total cost of glass bottles = number of glass bottles* cost of glass bottles = maxB * (b-c)
maxA->number of plastic bottles = ( total rubles — total cost of glass bottles ) / cost of plastic bottle = ( n-maxB*(b-c) ) / a
Does anyone have the correct codes for this contest?
Problem A:
Why can't we say if b — c < a then ans = n / (b — c)? Why c is subtracted from n so the formula became (n — c) / (b — c)?
In case (b — c) < a and N >= b:
While the condition (N — b + c >= b) holds we have to do N -= b, N += c.
Say that we do those operations k times:
it's clear that (Nk — (b — c)) < b and Nk >= b, otherwise we would do more than k operations.
So, in the end we just do Nk -= b without Nk += c.
It means that we did k operations N = N — b + c and 1 operation N = N — b:
So, in order to calculate the result without case handling ( N -= (b — c) or N -= b )
we assume that we do k + 1 operations of this type: N = N — b + c.
But now we know that N has 1 extra c. so, that's why we subtract c from N.
Hope it makes sense.