626A - Robot Sequence
We can simulate Calvin’s path on each substring, and check if he returns to the origin.
Runtime: O(n3)
626B - Cards
Note that if we have exactly one card of each color, we can always make all three options (by symmetry). Thus, if we have at least one of each color, or at least two of each of two colors, we can make all three options. The remaining cases are: if we only have one color, that’s the only possible final card; if we have one of each of two colors, we can only make the third color; if we have at least two of one color and exactly one of a second, we can only make the second or third color (e.g. sample 2).
Runtime: O(1)
626C - Block Towers
There are a variety of ways to do this problem. Here is one way: if the answer is X, there must be at least n multiples of 2 below X, at least m multiples of 3 below X, and at least n + m multiples of 2 or 3 below X. These conditions are actually sufficient, so we need to find the smallest X such that 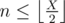 ,
, 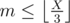 , and
, and 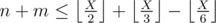 . We can do this with a linear search, or with an explicit formula.
. We can do this with a linear search, or with an explicit formula.
Runtime: O(1)
626D - Jerry's Protest
We do this algorithm in two phases: first, we compute the probability distribution of the difference between the winner and loser of each round. This takes O(n2) time. Then, we can iterate over the 2 differences which Andrew wins by and compute the probability that Jerry has a greater total using with suffix sums.
Runtime: O(n2 + amax2)
626E - Simple Skewness
We can show that any subset with maximal simple skewness should have odd size (otherwise we drop the larger middle element: this decreases the median by more than it decreases the mean, assuming the mean is larger than the median).
Let’s fix the median at xi (in the sorted list), and set the size of the set to 2j + 1. We’d like to maximize the mean, so we can greedily choose the largest j elements below the median and the largest j elements above the median: xi - j, ..., xi - 1 and xn - j + 1, ..., xn.
Now, notice that by increasing j by 1, we add in the elements xi - j - 1 and xn - j, which decrease as j increases. Thus, for a fixed i, the overall mean is bitonic in j (it increases then decreases), so we can binary search on the marginal utility to find the optimum.
Runtime: 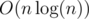
626F - Group Projects
This is a dynamic programming problem. Notice that the total imbalance of the groups only depends on which students are the maximum in each group and which are the minimum in each group. We thus can think of groups as intervals bounded by the minimum and maximum student. Moreover, the total imbalance is the sum over all unit ranges of the number of intervals covering that range. We can use this formula to do our DP.
If we sort the students in increasing size, DP state is as follows: the number of students processed so far, the number of g groups which are currently “open” (have a minimum but no maximum), and the total imbalance k so far. For each student, we first add the appropriate value to the total imbalance (g times the distance to the previous student), and then either put the student in his own group (doesn’t change g), start a new group (increment g), add the student to one of the g groups (doesn’t change g), or close one of the g groups (decrement g).
Runtime: O(n2k)
626G - Raffles
First, note that the marginal utility of each additional ticket in a single raffle is decreasing. Thus, to solve the initial state, we can use a heap data structure to store the optimal raffles.
Now, after each update, we can show that the distribution should not change by much. In particular, after one ticket is added to a raffle, Johnny should either remove one ticket from that raffle and place it elsewhere, not change anything, or, if the raffle was already full, put one more ticket in to keep it full. Similarly, after a ticket is removed, Johnny should either do nothing, remove one ticket to stay under the maximum, or add one ticket. (The proofs are fairly simple and involve looking at the “cutoff” marginal utility of Johnny’s tickets.) All of these operations can be performed using two heaps storing the optimal ticket to add and the optimal ticket to remove.
Runtime: 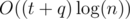










Thanks for this tutorial.
Hi, I would like to know, what kind of theory about probabilities and suffix sums I should read to have the bases to understand problem D editorial?. Thank you. I am asking for keywords to search about
You calculate the total number of the states of the game, which is (n * (n — 1) / 2) ^ 3. Then you calculate the number of the states which helps Jerry win. The answer is the second number / the first number.
While calculating the second number, we first get how many times each difference appear in the difference array. And then we iterate through the array over 2 differences (which are the first and second round), now we only need to find how many number bigger than X exist in this array, and a SUFFIX sum of this array helps.
EDIT: it should have been suffix sum. sorry for the mistake.
The total number should be (n * (n — 1) / 2) ^ 3.
now we only need to find how many number bigger than X
What is X ? and why do you use prefix sum?
X is sum of the "2 differences" of the previous rounds. We can use prefix sum to calculate how many numbers are less than or equal to X, and the result is [total number of possible matches] — [prefix sum]. Or you can use suffix sum to calculate it directly.
I meant that we only had to deal with finding number of elements which are bigger than X in an array.
Specifically, X in this problem stands for the sum of 2 differences you iterated on.
I think I understood the solution. I will review from simple to complex.
In N ways. Each way has one different number.
A total of N*(N-1) ways because we can not repeat numbers otherwise it would be N*N
We can say that each of the N*(N-1) chances, will have a opposite twin. For example for the case first=2, second=3, I can say it exist another case first=3, second=2. So on this view each twin group has two chances and in one of these the first beat the second. The final conclusion is that in the half of the ways of choosing two cards it happens that the first wins against the second. N*(N-1)/2
In each game there is a custom winner. We must note that it doesn't not affect who is the winner in each game, only the fact that in only 50% of the chances of each game it will occur that the target player wins. So as in each game it exists N*(N-1)/2 games where our target player wins against the other. The total amount of chances is (N*(N-1)/2)^3
The statement says that A wins 2 games, B wins 1, but then that the sum of B numbers i higher that the sum of A games. This is equivalent to say that first A wins the two first games and the sum of the difference of these two games is less that the difference number that B has to win the third game against A.
So first we'll get the frequency of each difference to occur in the first game. We can get it in O(N*N) if we iterate about each possible number for the first, and then about each possible second number that must be lower than first (because A wins the first game). So we have just calculated how many times a difference can occur over the total amount of different chances for one game. The cool idea is that if we iterate about each pair of difference values then we would be building all the differences for a pair of games that can exist. As we know the frequency of each of these two differences we can also calculate the amount of pair of games that has that two differences (Afreq * Bfreq) over the amount of possible ways of making these two games (N*(N-1)/2). But this is not enough. We need to get of these amount of games that has these two differences, how many of them will be followed by a game that its difference is higher than the sum of the two differences. We can use again the frequency array to the that number!! By iterating it from Adif+Bdif to the last number and sum all the frequencies, or faster, by first computing in O(N) how many games will have a difference higher than any X difference value. So If we multiply the values of Afreq*Bfreq and the amount of games that has a difference higher than Adif+Bdif We would get the amount of games where the first two get these two differences and then are followed by a game that has a higher difference than the sum of the first two. If we sum all the values of each pair of possible difference values for the first two games we will get the amount of different games that make valid what statement says, over the total amount of three games that is (N*(N-1)/2)^3. If we divide the two numbers we get the answer!
So that's all! I will try to code it EDIT: Yay! It works! 16024610 I tried to make it as clear as possible
How did you arrive at (n * (n — 1)) ^ 3? Edit. Correct me if I'm wrong. First two rounds Andrew can take n balls, but Jerry should now only take n-1 in order to lose, and in the third round it's the other way around. So for each round there's n*(n-1) such instances. Edit2. But since we count number of ways to do that, shouldn't it be nC2 for each round. It's also reflected in your code where you take (n * (n — 1) / 2) ^ 3?
Yes you are right, sorry for making a confusion. The
/2was gone while copy-pasting.Another solution for B: By realizing that you don't need more than 2 cards of each type, you can reduce size of string s less than or equal to 6, and it's possible to run a brute-force to find the final cards.
My submission: 16012250
Problem
Bcan be solved also by dynamic programming or bfs .Can anyone describe dynamic programming OR DFS based solution for Problem B?
all possible search space is 200*200*200 which you can try it all using DFS,BFS.
you have 6 option in each move so just try them all, and any time if you reach only one color save it.
Code with BFS, it's a little messy but you will get the idea. http://codeforces.com/contest/626/submission/16004077
Here is a BFS solution :
http://codeforces.com/contest/626/submission/15997121
Here is what I did for D, The denominator was obvious, (n*(n-1)/2)^3 (All game states possible where Andrew gets 2 higher and Jerry gets 1 higher) So basically, Let these be the balls picked Andrew -> a,b,c Jerry -> d,e,f
Where a>d, b>e, and f>c, but since the total of d+e+f should be greater than a+b+c hence, f-c > b-e + d-a
So my diff arrays stores the count of all differences possible after sorting the array, After which, we can mantain a defeats array (def), So def[x] stores the number of pairs that can be defeated by a (f-c) greater than x. After which I simply iterate lower differences for every diff[i], and cumilate the def of each j<i, to the number of ways. Now ways would be the numerator.
626D Code
Great explanation! But can't understand why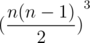 instead of
instead of 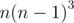 .
.
BTW Probably there should be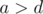 instead of
instead of 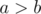
How many ways can you take two numbers from n numbers each round?
nC2.That's
n!/((n-2)!*2!), i.en(n-1)/2Like @DVRazor mentioned, we need to pick 2 numbers out of N, and since we don't care about order, since the person who gets the greater number is already decided, hence, nC2, and not nP2.
Also, yes. I meant a>d, thanks for the correction. Edited.
Problem B has a neat solution, I've found here 15992405. If the string consists only of one card type, then it's the answer, otherwise we count number of cards of each type in the string, if it's not equal to n-1 where n — length of a string, then we can get it at the end.
I didn't get this part in explanation of F "Moreover, the total imbalance is the sum over all unit ranges of the number of intervals covering that range. We can use this formula to do our DP." What do you mean by unit ranges of number of intervls?
That should be parsed as:
First sort the students by time to finish their piece.
Unit ranges are the differences between time of the (i - 1)-th and the i-th student. In the DP solution you have g open intervals. If you are about to add the i-th student you are expanding all open intervals (they ended in ai - 1, now they`ll end at ai). So, after you add the i-th student the total imbalance is increased by g * (ai - ai - 1) because each open inteval grows ai - ai - 1.
Let me know if I was not clear enough.
Can't understand why each interval is expanding? But each element can only be in one interval, right?
We are expanding each open interval because we are are adding only Unit ranges in each DP state.For eg.:
Suppose there is an open interval with max element a(i-2) and we want a grouping to be considered such that the above interval has next element a(i) in it.Thus we have to add a total imbalance of a(i) — a(i-2) . And since we have added imbalance of a(i-1) — a(i-2) (though element a(i-1) is not in the interval)earlier we only need to add imbalace of a(i) — a(i-1).
Thank you so much, now I see what does "unit ranges" means
Please someone explain the solution for problem E in more detail (may be with some examples or mathematical formulas).
A question regarding problem C.
How does dropping the
largestmiddle element decrease the median? It could also increase it, if the different with the next element is much greater than the difference with the previous one.Could you please elaborate on that?
You might have misunderstood the sentence I think.
Dropping the bigger median would leave the smaller one as the new median.
A quick example:
[1, 2, 3, 4] => Median = (2 + 3) / 2 = 2.5
(Drop 3)
[1, 2, 4] => Median = 2
Yes indeed, I've understood that sentence completely another way :) Thanks!
Can anyone explain please problem F : why we add (g + 0, + 1, -1) * (a[i] — a[i — 1]) , if we insert current a[i] only in one group ?
Does someone know if this solution for problem E is correct? It tests all sizes of the subset for the first 1000 distinct medians and for other possible medians it tests sizes smaller than 1000.
Kinda heuristic optimization in SQRT-decomposition style. I'm also very interested whether the hack-test exist.
In problem E, how do we prove that the overall mean is bitonic in j?
Also, can we say that if for some median a[i], the optimum length(for maximum mean) is 2*j+1; then for median a[i+1], the optimum length <= 2*(j+1)+1? This solution uses two-pointer with this idea.
I also used a similar idea, but during the contest I had a terrible logic bug which was hard for me to detect, then I realized what was wrong, anyways the main idea is the following, if the median is x[i], and lets say we are taking all elements from [l,i] and [r,N) into the optimal sequence, of course i-l=N-r.
Then for x[i+1], if the optimal answer requiered a smaller l, it would also imply a smaller r, both of the values in those positions would be smaller or equal than the current values in positions l and r, respectively, because of that we realize there don't exist two numbers which if we add them to the sequence we would get a higher average, because if they existed we would have already have them in x[i], as such if what we have in x[i] is optimal, then by moving l to the left in x[i+1] we would only be decreasing the skewness.
Not sure if I explained it correctly, at least that's what I though during the contest, but sadly my condition see if I should move l to the right or not was wrong, I was comparing it to the skewness of the previous i, instead of comparing it to the skewness gained by increasing l.
Heres my submission: 16028701
I think the following shows the mean is bitonic. Let A_j be the cumulative average with 2*j+1 values, we note that A_j is a weighted average of A_{j-1} and x_j:=(a[i-j]+a[N-j])/2.
Then A_j will be strictly less than A_{j-1} only when x_j < A_{j-1}. At the first point where this happens, we will get x_j < A_j < A_{j-1}. But then x_{j+1} <= x_j < A_j, so we will also have x_{j+1} < A_{j+1} < A_j, so the A_j will continue decreasing strictly by induction.
Can somebody explain problem F's editorial "we first add the appropriate value to the total imbalance (g times the distance to the previous student)" . Why is it g times the distance from the previous student? Shouldn't it be different for different cases described in the editorial?
The problem C What does it mean by "and at least n + m multiples of 2 or 3 below X" ?
if n==1 and m==1, the answer should be 3 but (n+m)*2=4, (n+m)*3=6, they aren't below 3
So can someone explain this? Thanks
2 is a multiple of 2, 3 is a multiple of 3, so we have 2 multiples of 2 or 3 below 3.
Thanks, but this can be explained as "if the answer is X, there must be at least n multiples of 2 below X, at least m multiples of 3 below X"
still don't get it "and at least n + m multiples of 2 or 3 below X"
For example, n = 3, m = 2. If X = 6, there are 3 multiples of 2 (2, 4, 6) and 2 multiples of 3 (3, 6) below 6, but X = 6 is not a correct answer. Number of multiples of 2 or 3 below 6 is just 4 (2, 3, 4, 6) which is less than n+m=5.
please explane me why set{2 3 4 6} multiply with 4? how u got 4?
Hi. In the third inequality, I didn't understand why its an inequality instead of an equality. Shouldn't the number of multiples of 2 or 3 be exactly equal to n + m?
Never mind. Got it.
In fact, I think I don't get the -X/6 part
Let A be the set of multiples of 2, B be the set of multiples of 3 below X.
Number of multiples of 2 or 3: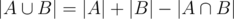 . Here
. Here  is the set of multiples of both 2 and 3, which are multiples of 6.
is the set of multiples of both 2 and 3, which are multiples of 6.
WOW, thank you for putting this so simple! Finally understood
Someone in my room has an O(n) solution for Problem A: http://codeforces.com/contest/626/submission/15999516
Can someone explain how it works?
Hey, I did something similar I believe, But in n^2. 626A Code It is pretty self explanatory, So, I kept a track of the x and y positions and then used a n^2 loop to see the number of times it repeats. What this person did instead was he mantained a map with (x,y) as key. So in O(n), he had the number of times any position is reached. Next he just iterated this map and added val*(val-1)/2 , where val is the number of times key (x,y) repeated.
Thanks, but the part I don't get is why for each
(x, y)that is visited (lets say forktimes), it addsC(k-1, 2)possible answers to the ways we can choose substrings that start and end at(0, 0)?So, let's say you reached a point (x,y) 4 times. So your map with key(x,y) will have the value 4. Let's say for the sake of understanding, that these 4 values were at Steps 1 3 5 and 7. So we have 4 options where we can choose 2 from. But the key here is, that since our choices are unordered (first number has to be smaller than second, for the substring), we use nC2 and not nP2.
Actually it's .
.
Well, he could've used unordered_map and it would be O(n)
Could someone, please, explain the following code: solution to 626C — Block Towers?
It looks damn beautiful, but I can't comprehend the whole idea behind it :(
You do binary search to find the answer. For that you need to check whether a candidate (here: mid) is ok. How to do it? Firstly you count number of sizes divisble by 3 but not by 2 (x3) and then similarly x2. Then you have some sizes that are divisble by 6 remaining- you can use them to either of groups and you only have to check if there are sufficiently many of them.
If you want to see a solution with the same idea but without binary search, see this one
Thank you.
One more question :)
Do you know how the upper bound is chosen to be
u = (n + m) * 6? Specifically, I don't understand the multiplier6.So let's show a constuction that uses only those numbers from 1.. 6*(n+m):
Those sets are disjoint and each of them consists of n+m numbers what is enough for us. Obviously, those multiplier 6 is not the tightest one, but who cares — it's under log from bin_search :)
Ok, now I understand the thought pattern behind this number :)
Lol, I pretty much overkilled problem B. I used 3 DPs — dpR[cntr][cntb][cntg], dpB[cntr][cntb][cntg] and dpG[cntr][cntb][cntg] which tell me whether I can remain with each color if I have cntr 'R's, cntb 'B's and cntg 'G's :D
I won't consider this an overkill. This solution is very straight forward and the very first solution came in my mind when I saw the problem. On the other hand, the other solution depends on some observations which may take some time to come up with.
Another solution to problem E which complexity is O(n):16032191 For each x(i) in the sorted list, put x(i) and x(n-length+1) to the set(current set size is length*2+1), continually remove two elements from the set until the mean of these two elements is larger than mean of overall elements in the set.
why " continually remove two elements from the set until the mean of these two elements is larger than mean of overall elements in the set." Is there any proof?
Problem A can be done with O(n^2) Here is the link: http://codeforces.com/contest/626/submission/15994678
Someone has described linear solution — link
can anyone prove it? Problem E: - We can show that any subset with maximal simple skewness should have odd size (otherwise we drop the larger middle element: this decreases the median by more than it decreases the mean, assuming the mean is larger than the median).
I don't why 。。。。 THANKS !
Assume for the sake of contradiction that a subset of size n (n ≥ 2 even) is maximal. Then, let μ be the mean, let x1 and x2 be the center elements, and let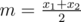 be the median. We know that μ - m ≥ 0, as this is maximal. Now, after dropping x2, the median decreases to x1 by
be the median. We know that μ - m ≥ 0, as this is maximal. Now, after dropping x2, the median decreases to x1 by 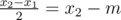 . The mean decreases to
. The mean decreases to 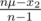 , which is a decrease by
, which is a decrease by 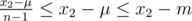 . Thus, the median decreases by more than the mean, so dropping x2 made it a better subset, a contradiction.
. Thus, the median decreases by more than the mean, so dropping x2 made it a better subset, a contradiction.
Can someone please explain the dp solution of F in little more detail?
Let's define a[i] : i'th person's value and dp[i][j][k] : when i'th person get in, and there are j groups left "open", k is the total imbalance. Here, "open" means that more people can(must) get in that group. As defined (dp), we cannot exactly figure out minimum value in each group. So, we should accumulate value despite not included in some group. For example, we can write one of the repetitions like this.
dp[i+1][j+1][k+j*(a[i+1]-a[i])]=dp[i][j][k].
It means that when (i+1)'th person get in "new group" and let it still "open". And the reason I accumulated j*(a[i+1]-a[i])is that each group is still "open", so it must receive more people, so when they are included, we can apply sum of imbalance by just adding another (a[p+1]-a[p]) since I've been doing a[i]+(a[i+1]+a[i+2]....values are included but not in group in reality+....+a[p])+a[p+1]
another case is dp[i+1][j][k+j*(a[i+1]-a[i])=dp[i][j][k]
It symbolizes (i+1)'th person get in "new group" and close that group immediately. Likewise, we can write two more. when (i+1)'th person get in one of the existed groups but not closing it, and get in one of the existed groups and close that group. we can get answer by seeing dp[n][0][0~max]. Start at dp[1][0][0]=1, dp[1][1][0]=1. Hope it'll be of help.
http://codeforces.com/contest/626/submission/19043064
Can someone help and point out where is my flaw for test case 12? :/
I tried to keep to long long instead of a double for the final result to evade floating point issues, but it seems that I have considered some of the boundary cases wrongly.
Problem C can be solved using a binary search code 87427076