1. Clothes (A Div-2)
In this problem constraints are allow to look throw all triples of clothes. For every triple one can check if all elements of tripe areturn out to match with others, and anong those triples find one whith minimal cost.
2. Sum of digits (B Div-2)
Initial number consist of no more then 100000 digits. Therefore after first transform resulting number will be no more then 900000, and then it will constist of no more then 6 digits. Thus after next transform number will be no more then 54 and so it will be two-digit or one-digit. Sum of digits of a two-digit number no more, then 18, and sum of digit of such number no more, then 9.
Thus Gerald can't do nore, then 4 transforms. First transform one can implement one simple pass throw symbols of given string. Following operations take very little time.
3. Homework (C Div-2, A Div-1)
Lets count up the number of entries to string of every letter. Let Gerald choose x letter and lose them. Obvious thet if he lose x rarest letters then overall number of losed letter do not increase, and then if he can lose some x lettes, he can lose x rarest ones. Thus it's easy to determine if Gerald can loses x letters. And now to calculate the answer one only need to find the minimal such x, so Gerald can lose x letters.
4. Buses (D Div-2, B Div-1)
For every slop from 0 to n lets calculate kx - number of ways come to them. Consider the i-th bus. Number of ways come to stop ti applied i-th bus is uqual to number of way to embus to i-th bus.
One can embus to i-th bus on the stops si, si + 1, ..., ti - 1. Thus number of ways come to stop ti in the i bus is equal to sum ksi + ksi + 1 + ... + kti - 1. Finally, lets note that overall number of way to come to stop ti is the sum of numbers of ways to come to stop ti on every bus.
It's remained two problems. First problem: 0 ≤ n ≤ 109. Therefore all kx not climb in memory limit. But we need to know only non-zero kx. For instance, one can gripe coordinates: create list of all occured stops (and also stops 0 and n), sort this list, delete the repeated stops and replace all numbers of stops they indexes in this list. After this operations all number of stops not exceed 200001, and all kx are climb to the memory.
Second problem: if we will use loop "for" for counting sum ksi + ksi + 1 + ... + kti - 1, asymptotic of time of working will be O(m^2). There is an easy way to solve this problem: one can create and update array sum[], such that sum[i] = k[0] + k[1] + ... + k[i - 1], by another words, sum[0] = 0, sum[i + 1] = sum[i] + k[i].
Then munber of ways to come to stop ti using bus i is equal to sum[ti] - sum[si].
So time complexity is O(m \cdot log(m)), memory complexity is O(m).
5. Vectors (E Div-2, C Div-1)
Lets formulate the problem in complex number.
Consider complex numbers a = xA + iyA, b = xB + iyB and c = xC + iyC. One can do operation A → A + C and A → iA.
If we apply this transform some times in some order to A, we will get number A· ik + aC + biC - cC - idC for some non-negative integers k, a, b, c, d or, in another words, A· ik + aC + biC for k = 0, 1, 2, 3 and some integers a, b. Since k can be equal only 0, 1, 2 or 3, sufficiently to get to know is one can to represent B - A, B - iA, B + A or B + iA in the form of aC + biC.
Then, how to determine, is one can to represent some complex number D in the such form? One can represent equation D = aC + biC in the form of linear real equation system:
a· xC - b· yC = xD
a· yC + b· xC = yD
To solve this system - is standart tehnical problem.
6. Castle (D Div-1)
Remunerate vertexes in such a way, that start Gerald vertex have got number 0.
Consider that vertex 0 is the root of tree, and lets consider its children. Let Gerald first go to vertex x. Then he must to travel throw hole subtree, otherwise he will not visit all vertex in subtree. Then he come back to 0 and go to some next its child.
Lets try to calculate looked for value for hole tree when we know all subtree values. If we can to do it, we can solve problem using dynamyc programming on the tree.
Lets vertex 0 have n children. Lets i-th subtree have ki offspring (inclusive i-th child of 0).
Let the hole tree consist of N vertexes.
Lets Ti is the doubled sum of lenght all edges in i-th subtree, inclusive edge between 0 and its i-th child. It is the time to travel throw hole i-th subtree, starting in 0 and returning to 0.
Finally, lets ti is answer to problem on i-th subtree. At once we add to this time length of edge between 0 and its i-th child.
Lets Gerald travel throw all subtrees in order 1, 2, ..., n. What is average time of finding the treasure?
Treasure can be in first subtree with probability 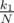 . Then average time of finding the treasure will be t1.
. Then average time of finding the treasure will be t1.
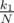 . Then average time of finding the treasure will be t1.
. Then average time of finding the treasure will be t1.Treasure can be in second subtree with probability 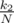 . Then average time of finding the treasure will be T1 + t2.
. Then average time of finding the treasure will be T1 + t2.
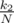 . Then average time of finding the treasure will be T1 + t2.
. Then average time of finding the treasure will be T1 + t2.And so on. Thus, average time of finding the treasure will be

Can we decrease this time? Lets swap i and i + 1 subtrees. Then item ki + 1Ti disappear from sum and appear item kiTi + 1. Sum will chenge to kiTi + 1 - ki + 1Ti. Sum will decrease, if kiTi + 1 - ki + 1Ti < 0, in ather words 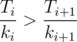 .
.
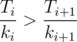 .
.Therefore, one can't decrease average time, if subtrees are sorted by increasing value 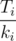 .
.
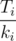 .
.So, we must to sorted trees in this order and traveling from them in this order.
7. Candies and Stones. (E Div-1)
Essence of problem is that there is a board n × m in cell of wich placed numbers. And one must go from cell (0, 0) to cell (n - 1, m - 1), doing moves to one cell up and right (that is, increasing by 1 on of coordinates), maximizing sum o number on the cell in the path.
Gerald's problems is determine m + n - 1 cells of optimal path. Lets start with search one, middle cell. Lets 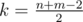 . What cell of board can be k-th in path? It is cell, sum of coordinate of wich is equal to k, thus, it is diagonal of doard. And then we can calculate, what maximum sum Gerald can collect, came to every cell in the diagonal, by dynamic programming in lower triangle. And the same way, we can calculate, what maximum sum Gerald can collect, came to cell (n-1,m-1), starting from every cell in the diagonal. Sumed up this to values, we calculate, what maximum sum Gerald can collect, came to from cell (0, 0) to cell (n - 1, m - 1), travel throw every cell in the diagonal. And now we will find cell (x, y), in wich maximum is reached. It is k-th cell of the path. We used time O((n + m)2) and memory O(n + m).
. What cell of board can be k-th in path? It is cell, sum of coordinate of wich is equal to k, thus, it is diagonal of doard. And then we can calculate, what maximum sum Gerald can collect, came to every cell in the diagonal, by dynamic programming in lower triangle. And the same way, we can calculate, what maximum sum Gerald can collect, came to cell (n-1,m-1), starting from every cell in the diagonal. Sumed up this to values, we calculate, what maximum sum Gerald can collect, came to from cell (0, 0) to cell (n - 1, m - 1), travel throw every cell in the diagonal. And now we will find cell (x, y), in wich maximum is reached. It is k-th cell of the path. We used time O((n + m)2) and memory O(n + m).
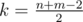 . What cell of board can be k-th in path? It is cell, sum of coordinate of wich is equal to k, thus, it is diagonal of doard. And then we can calculate, what maximum sum Gerald can collect, came to every cell in the diagonal, by dynamic programming in lower triangle. And the same way, we can calculate, what maximum sum Gerald can collect, came to cell (n-1,m-1), starting from every cell in the diagonal. Sumed up this to values, we calculate, what maximum sum Gerald can collect, came to from cell (0, 0) to cell (n - 1, m - 1), travel throw every cell in the diagonal. And now we will find cell (x, y), in wich maximum is reached. It is k-th cell of the path. We used time O((n + m)2) and memory O(n + m).
. What cell of board can be k-th in path? It is cell, sum of coordinate of wich is equal to k, thus, it is diagonal of doard. And then we can calculate, what maximum sum Gerald can collect, came to every cell in the diagonal, by dynamic programming in lower triangle. And the same way, we can calculate, what maximum sum Gerald can collect, came to cell (n-1,m-1), starting from every cell in the diagonal. Sumed up this to values, we calculate, what maximum sum Gerald can collect, came to from cell (0, 0) to cell (n - 1, m - 1), travel throw every cell in the diagonal. And now we will find cell (x, y), in wich maximum is reached. It is k-th cell of the path. We used time O((n + m)2) and memory O(n + m).Then we make recursive call on subproblems. In other word, will find optimal path from cell (0, 0) to cell (x, y) and from cell (x, y) to cell (n, m).
It is evident, this solution take memory O(n+m). Why it tkae time O((n+m)^2)?
Lets n + m is r.
Once we are find middle cell of path of length k. Twice we are find middle cell of path of length  . Four times we are find middle cell of path of length
. Four times we are find middle cell of path of length 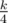 . And so on. Therefore, time of program working will be
. And so on. Therefore, time of program working will be 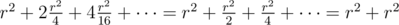 . Thus, this solution take time O((n + m)2).
. Thus, this solution take time O((n + m)2).
 . Four times we are find middle cell of path of length
. Four times we are find middle cell of path of length 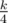 . And so on. Therefore, time of program working will be
. And so on. Therefore, time of program working will be 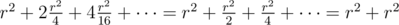 . Thus, this solution take time O((n + m)2).
. Thus, this solution take time O((n + m)2).










I think you are right.^_^
so the space is still
O(nm), but you split it in half (or a quarter), so that it takes25MB, and then compute the rest? Feels like the recursive solution, but you split it only once or so and the dp is simpler (its not a diagonal row). I'm not sure if i get your idea.I came up with a very similar solution. First I find all the cells of the middle diagonal and then use DP to find the cell inside the diagonal that also belongs to the optimal path. Then using DP and a bitset<200000000> I find the optimal path from the upper left corner to the cell in the diagonal (this is the first half). I do the same thing to find the optimal path from the cell in the diagonal to the lower right corner (this is the second half). I join both halves and the full path is totally recovered. Here is my submission: http://codeforces.com/contest/101/submission/31324561
tkae should be take.
I think this is the Smallest Solution for the B problem
Nice solution... a little way to make it faster is by adding ths line before for loop :-
s.erase(remove(s.begin(),s.end(),'0'), s.end());
This helps in removing the unwanted '0' from the string which dosent add to change the sum
what is the use of subtracting v from the lower_bound iterato vector<pair<int,int> v ; int l = lower_bound(v, v + i, pii(v[i].second, 0)) — v;
I keep running into problems where I hit a wall because the input is too big for what I know how to handle in Java.
Question B is one of those problems. I am using longs and they still aren't long enough for the digits in the input.
Is this a sign that the answer has to be found with another language or is there a technique I don't know about?
Try using strings instead :)
I am not getting problem D.
Im also finding the solution very difficult to understand
Here is how I solved:
Let dp[x] be the number of ways to get to stop x. dp[0] = 1. So, for every bus i, you can do: $$$dp[t_i] = \sum_{s_i \leq j < t_i} dp[j]$$$. But we have a problem here, since $$$1 \leq t_i \leq 10^9$$$. You can use coordinate compression to handle this. You also can't compute this sum naively. I did it with a segment tree. Here is my submission for details.
242922518 my approach to the problem was to create a string consisting of integer characters, and adding the integer value of them to the variable called sum and after the summation is finished, converting the sum to the string and go on while the string.size() is bigger than 1 since the number we want is one digit.
sorry for my bad english, I hope this solution helps someone someday. Gl to all on their journeys.
I like the B problem easy implementation but i strugled to find the solution
can anyone provide the solution for Homework (C Div-2, A Div-1) i am a beginner to CP but this question looked interesting for greedy algorithm. i am having some difficulty in implementing it. Answer to this will help me a lot, Thanx:)