Author thanks adamax for translation this article into English.
Introduction
After Codeforces Beta Round #11 several participants expressed a wish to read something about problems similar to problem D of that round. The author of this article, for the purpose of helping them, tried searching for such information, but to his surprise couldn't find anything on the Internet. It is not known whether the search was not thorough or there's really nothing out there, but (just in case) the author decided to write his own article on this topic.
In some sense this article may be regarded as a tutorial for the problem D from Beta Round #11.
In this article quite well-known algorithms are considered: the search for optimal Hamiltonian walks and cycles, finding their number, check for existence and something more. The so-called "dynamic programming over subsets" is used. This method requires exponential time and memory and therefore can be used only if the graph is very small - typically 20 vertices or less.
DP over subsets
Consider a set of elements numbered from 0 to N - 1. Each subset of this set can be encoded by a sequence of N bits (we will call this sequence "a mask"). The i-th element belongs to the subset if and only if the i-th bit of the mask equals 1. For instance, the mask 00010011 means that the subset of the set [0... 7] consists of elements 0, 1 and 4. There are totally 2N masks, and so 2N subsets. Each mask is in fact an integer number written in binary notation.
The method is to assign a value to each mask (and, therefore, to each subset) and compute the values for new masks using already computed values. As a rule, to find the value for a subset A we remove an element in every possible way and use values for obtained subsets A'1, A'2, ... , A'k to compute the value for A. This means that the values for Ai' must have been computed already, so we need to establish an ordering in which masks will be considered. It's easy to see that the natural ordering will do: go over masks in increasing order of corresponding numbers.
We will use the following notation:
bit(i, mask) - the i-th bit of mask
count(mask) - the number of non-zero bits in mask
first(mask) - the number of the lowest non-zero bit in mask
(a?b: c) - returns b if a holds, or c otherwise.
The elements of our set will be vertices of the graph. For the sake of simplicity we'll assume that the graph is undirected. Modification of the algorithms for directed graphs is left as an exercise for the reader.
1. Search for the shortest Hamiltonian walk
Let the graph G = (V, E) have n vertices, and each edge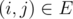 have a weight d(i, j). We want to find a Hamiltonian walk for which the sum of weights of its edges is minimal.
have a weight d(i, j). We want to find a Hamiltonian walk for which the sum of weights of its edges is minimal.
Let dp[mask][i] be the length of the shortest Hamiltonian walk in the subgraph generated by vertices in mask, that ends in the vertex i.
The DP can be calculated by the following formulas:
dp[mask][i] = 0, if count(mask) = 1 and bit(i, mask) = 1;
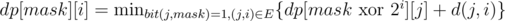 , if count(mask) > 1 and bit(i, mask) = 1;
, if count(mask) > 1 and bit(i, mask) = 1;
dp[mask][i] = ∞ in other cases.
Now the desired minimal length is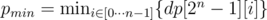 . If pmin = ∞, then there is no Hamiltonian walk in the graph. Otherwise it's easy to recover the walk itself. Let the minimal walk end in the vertex i. Then the vertex j ≠ i, for which
. If pmin = ∞, then there is no Hamiltonian walk in the graph. Otherwise it's easy to recover the walk itself. Let the minimal walk end in the vertex i. Then the vertex j ≠ i, for which 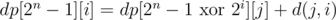 , is the previous vertex in the path. Now remove i from the set and find the vertex previous to j in the same way. Continuing this process until only one vertex is left, we'll find the whole Hamiltonian walk.
, is the previous vertex in the path. Now remove i from the set and find the vertex previous to j in the same way. Continuing this process until only one vertex is left, we'll find the whole Hamiltonian walk.
This solution requires O(2nn) of memory and O(2nn2) of time.
2. Finding the number of Hamiltonian walks
Let the graph G = (V, E) be unweighted. We'll modify the previous algorithm. Let dp[mask][i] be the number of Hamiltonian walks on the subset mask, which end in the vertex i. The DP is rewritten in the following way:
dp[mask][i] = 1, if count(mask) = 1 and bit(i, mask) = 1;
 , if count(mask) > 1 and bit(i, mask) = 1;
, if count(mask) > 1 and bit(i, mask) = 1;
dp[mask][i] = 0 in other cases.
The answer is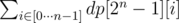 .
.
This solution requires O(2nn) of memory and O(2nn2) of time.
3. Finding the number of simple paths
Calculate the DP from the previous paragraph. The answer is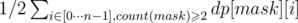 . The coefficient 1 / 2 is required because each simple path is considered twice - in both directions. Also note that only paths of positive length are taken into account. You can add n zero-length paths, of course.
. The coefficient 1 / 2 is required because each simple path is considered twice - in both directions. Also note that only paths of positive length are taken into account. You can add n zero-length paths, of course.
This solution requires O(2nn) of memory and O(2nn2) of time.
4. Check for existence of Hamiltonian walk
We can use solution 2 replacing the sum with bitwise OR. dp[mask][i] will contain a boolean value - whether there exists a Hamiltonian walk over the subset mask which ends in the vertex i. DP is the following:
dp[mask][i] = 1, if count(mask) = 1 and bit(i, mask) = 1;
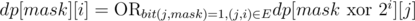 , if count(mask) > 1 and bit(i, mask) = 1;
, if count(mask) > 1 and bit(i, mask) = 1;
dp[mask][i] = 0 in other cases.
This solution, like solution 2, requires O(2nn) of memory and O(2nn2) of time. It can be improved in the following way.
Let dp'[mask] be the mask of the subset consisting of those vertices j for which there exists a Hamiltonian walk over the subset mask ending in j. In other words, we 'compress' the previous DP: dp'[mask] equals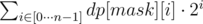 . For the graph G write out n masks Mi, which give the subset of vertices incident to the vertex i. That is,
. For the graph G write out n masks Mi, which give the subset of vertices incident to the vertex i. That is, 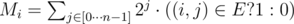 .
.
DP will be rewritten in the following way:
dp'[mask] = 2i, if count(mask) = 1 and bit(i, mask) = 1;
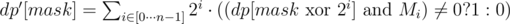 , if count(mask) > 1;
, if count(mask) > 1;
dp'[mask] = 0 in other cases.
Pay special attention to the expression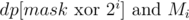 . The first part of the expression is the subset of vertices j, for which there exists a Hamiltonian walk over the subset mask minus vertex i, ending in j. The second part of the expression is the set of vertices incident to i. If these subsets have non-empty intersection (their bitwise AND is non-zero), then it's easy to see that there exists a Hamiltonian walk in mask ending in the vertex i.
. The first part of the expression is the subset of vertices j, for which there exists a Hamiltonian walk over the subset mask minus vertex i, ending in j. The second part of the expression is the set of vertices incident to i. If these subsets have non-empty intersection (their bitwise AND is non-zero), then it's easy to see that there exists a Hamiltonian walk in mask ending in the vertex i.
The final test is to compare dp[2n - 1] to 0.
This solution uses O(2n) of memory and O(2nn) of time.
5. Finding the shortest Hamiltonian cycle
Since we don't care at which vertex the cycle starts, assume that it starts at 0. Now use solution 1 for the subset of vertices, changing the formulas in the following way:
dp[1][0] = 0;
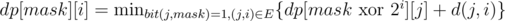 , if i > 0, bit(0, mask) = 1 and bit(i, mask) = 1;
, if i > 0, bit(0, mask) = 1 and bit(i, mask) = 1;
dp[mask][i] = ∞ in other cases.
So dp[mask][i] contains the length of the shortest Hamiltonian walk over the subset mask, starting at 0 and ending at i.
The required minimum is calculated by the formula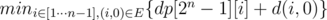 . If it equals ∞, there is no Hamiltonian cycle. Otherwise the Hamiltonian cycle can be restored by a method similar to solution 1.
. If it equals ∞, there is no Hamiltonian cycle. Otherwise the Hamiltonian cycle can be restored by a method similar to solution 1.
6. Finding the number of Hamiltonian cycles
Using ideas from solutions 5 and 2 one can derive a DP calculating the number of Hamiltonian cycles requiring O(2nn2) of time and O(2nn) of memory.
7. Finding the number of simple cycles
Let dp[mask][i] be the number of Hamiltonian walks over the subset mask, starting at the vertex first(mask) and ending at the vertex i. DP looks like this:
dp[mask][i] = 1, if count(mask) = 1 and bit(i, mask) = 1;
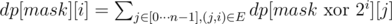 , if count(mask) > 1, bit(i, mask) = 1 and i ≠ first(mask);
, if count(mask) > 1, bit(i, mask) = 1 and i ≠ first(mask);
dp[mask][i] = 0 otherwise.
The answer is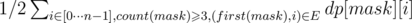 .
.
This solution requres O(2nn2) of time and O(2nn) of memory.
8. Checking for existence of Hamiltonian cycle
We can modify solution 5 and, using the trick from solution 4, obtain an algorithm requiring O(2nn) of time and O(2n) of memory.
Exercises
CFBR11D
CCTOOLS
P.S. This article may be extended and fixed in future. The author would be grateful for supplementing the Exercises section and for pointing out any mistakes and inaccuracies.
Introduction
After Codeforces Beta Round #11 several participants expressed a wish to read something about problems similar to problem D of that round. The author of this article, for the purpose of helping them, tried searching for such information, but to his surprise couldn't find anything on the Internet. It is not known whether the search was not thorough or there's really nothing out there, but (just in case) the author decided to write his own article on this topic.
In some sense this article may be regarded as a tutorial for the problem D from Beta Round #11.
In this article quite well-known algorithms are considered: the search for optimal Hamiltonian walks and cycles, finding their number, check for existence and something more. The so-called "dynamic programming over subsets" is used. This method requires exponential time and memory and therefore can be used only if the graph is very small - typically 20 vertices or less.
DP over subsets
Consider a set of elements numbered from 0 to N - 1. Each subset of this set can be encoded by a sequence of N bits (we will call this sequence "a mask"). The i-th element belongs to the subset if and only if the i-th bit of the mask equals 1. For instance, the mask 00010011 means that the subset of the set [0... 7] consists of elements 0, 1 and 4. There are totally 2N masks, and so 2N subsets. Each mask is in fact an integer number written in binary notation.
The method is to assign a value to each mask (and, therefore, to each subset) and compute the values for new masks using already computed values. As a rule, to find the value for a subset A we remove an element in every possible way and use values for obtained subsets A'1, A'2, ... , A'k to compute the value for A. This means that the values for Ai' must have been computed already, so we need to establish an ordering in which masks will be considered. It's easy to see that the natural ordering will do: go over masks in increasing order of corresponding numbers.
We will use the following notation:
bit(i, mask) - the i-th bit of mask
count(mask) - the number of non-zero bits in mask
first(mask) - the number of the lowest non-zero bit in mask
(a?b: c) - returns b if a holds, or c otherwise.
The elements of our set will be vertices of the graph. For the sake of simplicity we'll assume that the graph is undirected. Modification of the algorithms for directed graphs is left as an exercise for the reader.
1. Search for the shortest Hamiltonian walk
Let the graph G = (V, E) have n vertices, and each edge
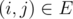 have a weight d(i, j). We want to find a Hamiltonian walk for which the sum of weights of its edges is minimal.
have a weight d(i, j). We want to find a Hamiltonian walk for which the sum of weights of its edges is minimal.Let dp[mask][i] be the length of the shortest Hamiltonian walk in the subgraph generated by vertices in mask, that ends in the vertex i.
The DP can be calculated by the following formulas:
dp[mask][i] = 0, if count(mask) = 1 and bit(i, mask) = 1;
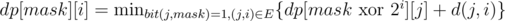 , if count(mask) > 1 and bit(i, mask) = 1;
, if count(mask) > 1 and bit(i, mask) = 1;dp[mask][i] = ∞ in other cases.
Now the desired minimal length is
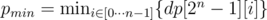 . If pmin = ∞, then there is no Hamiltonian walk in the graph. Otherwise it's easy to recover the walk itself. Let the minimal walk end in the vertex i. Then the vertex j ≠ i, for which
. If pmin = ∞, then there is no Hamiltonian walk in the graph. Otherwise it's easy to recover the walk itself. Let the minimal walk end in the vertex i. Then the vertex j ≠ i, for which 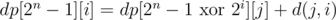 , is the previous vertex in the path. Now remove i from the set and find the vertex previous to j in the same way. Continuing this process until only one vertex is left, we'll find the whole Hamiltonian walk.
, is the previous vertex in the path. Now remove i from the set and find the vertex previous to j in the same way. Continuing this process until only one vertex is left, we'll find the whole Hamiltonian walk.This solution requires O(2nn) of memory and O(2nn2) of time.
2. Finding the number of Hamiltonian walks
Let the graph G = (V, E) be unweighted. We'll modify the previous algorithm. Let dp[mask][i] be the number of Hamiltonian walks on the subset mask, which end in the vertex i. The DP is rewritten in the following way:
dp[mask][i] = 1, if count(mask) = 1 and bit(i, mask) = 1;
 , if count(mask) > 1 and bit(i, mask) = 1;
, if count(mask) > 1 and bit(i, mask) = 1;dp[mask][i] = 0 in other cases.
The answer is
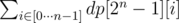 .
.This solution requires O(2nn) of memory and O(2nn2) of time.
3. Finding the number of simple paths
Calculate the DP from the previous paragraph. The answer is
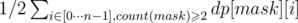 . The coefficient 1 / 2 is required because each simple path is considered twice - in both directions. Also note that only paths of positive length are taken into account. You can add n zero-length paths, of course.
. The coefficient 1 / 2 is required because each simple path is considered twice - in both directions. Also note that only paths of positive length are taken into account. You can add n zero-length paths, of course.This solution requires O(2nn) of memory and O(2nn2) of time.
4. Check for existence of Hamiltonian walk
We can use solution 2 replacing the sum with bitwise OR. dp[mask][i] will contain a boolean value - whether there exists a Hamiltonian walk over the subset mask which ends in the vertex i. DP is the following:
dp[mask][i] = 1, if count(mask) = 1 and bit(i, mask) = 1;
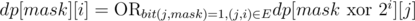 , if count(mask) > 1 and bit(i, mask) = 1;
, if count(mask) > 1 and bit(i, mask) = 1;dp[mask][i] = 0 in other cases.
This solution, like solution 2, requires O(2nn) of memory and O(2nn2) of time. It can be improved in the following way.
Let dp'[mask] be the mask of the subset consisting of those vertices j for which there exists a Hamiltonian walk over the subset mask ending in j. In other words, we 'compress' the previous DP: dp'[mask] equals
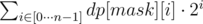 . For the graph G write out n masks Mi, which give the subset of vertices incident to the vertex i. That is,
. For the graph G write out n masks Mi, which give the subset of vertices incident to the vertex i. That is, 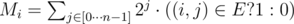 .
.DP will be rewritten in the following way:
dp'[mask] = 2i, if count(mask) = 1 and bit(i, mask) = 1;
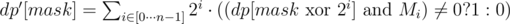 , if count(mask) > 1;
, if count(mask) > 1;dp'[mask] = 0 in other cases.
Pay special attention to the expression
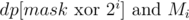 . The first part of the expression is the subset of vertices j, for which there exists a Hamiltonian walk over the subset mask minus vertex i, ending in j. The second part of the expression is the set of vertices incident to i. If these subsets have non-empty intersection (their bitwise AND is non-zero), then it's easy to see that there exists a Hamiltonian walk in mask ending in the vertex i.
. The first part of the expression is the subset of vertices j, for which there exists a Hamiltonian walk over the subset mask minus vertex i, ending in j. The second part of the expression is the set of vertices incident to i. If these subsets have non-empty intersection (their bitwise AND is non-zero), then it's easy to see that there exists a Hamiltonian walk in mask ending in the vertex i.The final test is to compare dp[2n - 1] to 0.
This solution uses O(2n) of memory and O(2nn) of time.
5. Finding the shortest Hamiltonian cycle
Since we don't care at which vertex the cycle starts, assume that it starts at 0. Now use solution 1 for the subset of vertices, changing the formulas in the following way:
dp[1][0] = 0;
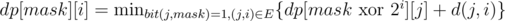 , if i > 0, bit(0, mask) = 1 and bit(i, mask) = 1;
, if i > 0, bit(0, mask) = 1 and bit(i, mask) = 1;dp[mask][i] = ∞ in other cases.
So dp[mask][i] contains the length of the shortest Hamiltonian walk over the subset mask, starting at 0 and ending at i.
The required minimum is calculated by the formula
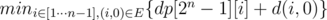 . If it equals ∞, there is no Hamiltonian cycle. Otherwise the Hamiltonian cycle can be restored by a method similar to solution 1.
. If it equals ∞, there is no Hamiltonian cycle. Otherwise the Hamiltonian cycle can be restored by a method similar to solution 1.6. Finding the number of Hamiltonian cycles
Using ideas from solutions 5 and 2 one can derive a DP calculating the number of Hamiltonian cycles requiring O(2nn2) of time and O(2nn) of memory.
7. Finding the number of simple cycles
Let dp[mask][i] be the number of Hamiltonian walks over the subset mask, starting at the vertex first(mask) and ending at the vertex i. DP looks like this:
dp[mask][i] = 1, if count(mask) = 1 and bit(i, mask) = 1;
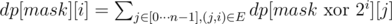 , if count(mask) > 1, bit(i, mask) = 1 and i ≠ first(mask);
, if count(mask) > 1, bit(i, mask) = 1 and i ≠ first(mask);dp[mask][i] = 0 otherwise.
The answer is
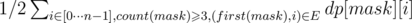 .
.This solution requres O(2nn2) of time and O(2nn) of memory.
8. Checking for existence of Hamiltonian cycle
We can modify solution 5 and, using the trick from solution 4, obtain an algorithm requiring O(2nn) of time and O(2n) of memory.
Exercises
CFBR11D
CCTOOLS
P.S. This article may be extended and fixed in future. The author would be grateful for supplementing the Exercises section and for pointing out any mistakes and inaccuracies.











For example
пусть пока повисит тут. потом, возможно, добавлю. возможно в новый раздел:)
Maybe I will view your problem in fiture article:)
it is very old paper:)
is an example problem for part 5.
Could you please further explain the recurrence in the first example (finding a shortest Hamiltonian walk)?
The following paper is potentially useful as reference:
"A Dynamic Programming Approach to Sequencing Problems" by Michael Held and Richard M. Karp, 1962. [citation, download]
It contains lots of preliminary analysis and at least the DP approaches described in 1. and 5. of your post. I believe the algorithm is actually called "Held–Karp algorithm" in academic literature, but it was described independently by Bellman et al. in another paper.
A list of optimal algorithms for TSP with better runtime complexity can be found here.
can't open first link it requires e-mail for link sites.can u help me and give pdf file?
Took me two seconds to find another PDF source: http://people.cs.vt.edu/~gback/ICPCHandbook/book/copiesfromweb/held-karp-jsiam-1962.pdf
you're welcome.
In 4th section's second dp formulation second part, the condition stated is count(mask)>1 only. Isn't bit(mask, i) == 1 condition should also be included?
can anybody give me link to its implemented code for any of the above part. Rest I got stuck at bit masking in implementation. Thanks in advance whoever will give link.
My solution for task D of CF beta round 11.
Btw,am i the only one who can't see the solution of others in this contest?i can't even open my solution.
me too, something is wrong today, I can't open submission code, including myself, now I can only open my "official" submissions.
Yes also just encountered this problem. Why I try to open my own solution I get "You are not allowed to view the requested page" error.
I actually have theory now for why this is. I think problem D might have been used in the VK Cup Finals — Trial Contest, and so they blocked solutions so we could not see submission from people in that contest.
In first Section, consider a graph with only two vertices and one edge of weight say w then the answer computed by the process, comes to be w but expected asnwer is 2*w as for a hamiltonian walk the starting and ending vertices must be same.
In the 7th section, how are those paths included in the answer where we use vertices v < first(mask). This means, if our bit representation of mask is 1101000, and we want to count no. of paths starting at first(mask)=3(3rd bit, 0-based indexing from right to left) and ending at vertex v=5(0-based indexing from right to left), how will paths like the one starting from vertex 3 to vertex 5 with vertex 0 on the way(and similar) be counted if we use the dp meaning given in section 7?
In a hamiltonian walk the vertices might repeat. On the other hand, in a simple path repetition of vertices is not allowed. How is it that using the same dp for ques 3 which was used for ques 2 works? Any insights would be highly appreciated.
i think it is actually hamiltonian 'path' and not hamiltonian 'walk'.
Isn't checking for hamiltonian path obvious when atleast 2 nodes are attached to each other?
Great Post. Cleared all the doubts regarding "Hamiltonian". Thanks a lot.
in problem 2, is the graph complete?
I think in the first two problem author is talking about Hamiltonian path, not about Hamiltonian walk. Please correct me if I am wrong. Thanks!
I think so.
Link to HackerEarth practice problems.
I noticed a minor issue(maybe typo) in the transition of the DP state in P4 : Checking the existence of the Hamiltonian walk in $$$O(2^{n} \cdot n)$$$, since I'm writing a comment anyway let me explain with a little more detail which smol idea help us optimize it from $$$O(2^{n} \cdot n^2)$$$ to $$$O(2^{n} \cdot n)$$$ .
Idea — Since we only need a binary (yes/no) answer for each vertex $$$j$$$ in $$$mask$$$ to see whether it can reach $$$i$$$, we can use mask $$$X$$$ to store all that information instead of using $$$j$$$ (which is iterating over all $$$n$$$), this saves us extra $$$O(n)$$$.
Def. — $$$dp'[mask]~=~X$$$, $$$X$$$ is a subset of the $$$mask$$$, where the set-bits in $$$X$$$ indicate the vertices that allow for a successful Hamiltonian Walk across $$$mask$$$ which ends at the set-bit vertex.
Transition — For $$$i$$$-th bit that is set in $$$mask$$$ , we need to know whether $$$dp'[mask \oplus 2^{i}]$$$'s successful Walks can reach $$$i$$$-th vertex, for that we need to precalculate $$$M_{i}$$$, $$$M_{i} = $$$ mask made of vertices that are incident to $$$i$$$. If $$$M_{i}$$$ and $$$dp[mask \oplus i]$$$ share vertices we can extend our successful Walk towards $$$i$$$ and set $$$dp'[mask]$$$'s $$$i$$$-th bit as $$$1$$$.
Base — $$$dp'[2^{i}] = 2^{i}$$$ for every $$$i \le n$$$.
I'm not really sure but shouldn't the part were you wrote " Mi= mask made of vertices that are incident to i . If Mi and dp[mask⊕i] share vertices " shouldn't it be mask xor pow(2,i) ?