150E - Freezing with Style
If there exists a path with the median ≥ k, for some k, then there exists a path with the median ≥ q, for each q ≤ k. That means we can use binary search to calculate the answer. So now the task is: is there any path with the median greater or equal to Mid ?
We will calc the edge as + 1 if it's wight ≥ Mid, or as - 1 in other case. Now we only need to check if there exists a path with legal length and the sum greater than or equal to zero.
Let's denote some node V as a root.
All paths can be divided into two types: that contains v, and that do not. Now we are to process all first-type paths and run the algorithm on all subtrees. That is so-called divide-and-conquer strategy.
We can trivially show that it is always possible to choose such vertex v that all it's subtrees will have size less than or equal to the size of the whole tree. That means that each node will be proccessed in LogN trees max.
So, if we solve the task for one level of recursion in O(F(N)), we'll solve it in time O(F(N) * log2(N)) on the whole.
First, lets get O(N * Log(N)). For each node we shall calc it's deepness, cost of the path to the root ans the first edge (the number of the root's subtree). It will be better now to use 2 and 0 as the edges costs, instead of -1 and 1. Now we shall process root's subtrees one by one. For each node we want to know if there exists a node u in any other subtree such that the
Unable to parse markup [type=CF_TEX]
and cost[v] - deep[v] + cost[u] - deep[u] ≥ 0. To do that we need to know the maximum of the function (cost[u] - deep[u]) with the deep values between max(0, L - deep[v]) and R - deep[v] inclusive. To achieve O(N * log(N)) you need only to use segment tree.To achieve an AC contestants were to write all code optimally, or to think of one more idea. It is possible to have O(N) on one level of recursion and O(N * log2(N)) in total if you sort roots subtrees in non-decreasing order and use any structure that can answer getmax query on all segments of length (R - L + 1) and all prefixes and suffixes.
Best of luck to you in upsolving this problem!
150D - Mission Impassable
In this problem you have to use dynamic programming. For our convenience we will calulate three type of values:
Best[l][r] — best result player can achieve on the segment [l, r].
Full[l][r] — best result player can achieve on the segment from [l, r] if he fully destroys it.
T[l][r][Len] — best result player can achieve on the segment from [l, r] and remain the palindrome of length len and only it.
Now solution:
Full[l][r]. Let's look which move will be the last. This will be removing the palindrome of length len and c[len] ≥ 0. What is the best result we can achieve? c[len] + T[l][r][len].
Best[l][r]. Either we will destroy all subtring from l to r, either there exists a letter which we did not touch. That means that all our moves lies fully to the left or fully to the rigth to that position. So Best[l][r] = Full[l][r] or Best[l][r] = Best[l][m] + Best[m + 1][r] for some m, l ≤ m < r.
T[l][r][len]. len = 0, len = 1 — two special cases, which is easy to solve without any dynamic. In other case, let's take a look on the left-most position. It either will lie in the result string or not. If not, then let's find the first position which does. Denote it as m (l < m ≤ r). Everything what lies to the left need to be fully deleted. So the answer is Full[l][m - 1] + T[m][r][len] (for l < m ≤ r). Similarly, for the right-most letters. If it does not lies in the result string we remove everything to the right and our result is T[l][m][len] + Full[m + 1][r] (for l ≤ m < r). The last option: both left-most and rigth-most letters lies in the result string. It is possible only if s[l] = s[r]. So our result is T[l + 1][r - 1][len - 2] (only if s[l] = = s[r]).
150C - Smart Cheater
First lets use the linearity of expected value and solve task independently for each passanger.
For each path segment (route between neighboring stations) we calculate expected value of profit in case we do not sell a ticket for this segment. In case we sell it the expectation of profit is 0.
Now we only need to find the subsegment of segment [a, b] of maximal sum for each passanger.
That's easy to do by the segment tree, we only need to calc four values for each node:
best — the maximal sum of elements on some subsegment
max_left — the maximal sum on prefix
max_right — the maximal sum on suffix
sum — the sum of all elements
150B - Quantity of Strings
We can offer you two solitions:
You can build a graph with positions in sting as a nodes and equality in any substring of length k as edges. Lets denote e the number of components in the graph. The answer is me.
Analyze four cases:
- k = 1 or к > n, the answer is mn.
- k = n, the answer is m(n + 1) / 2.
- k mod 2 = 1, any string like abababab... is ok, so the answer is m2.
- k mod 2 = 0, all symbols coincide and the answer is m.
150A - Win or Freeze
if Q is prime or Q = 1 than it's victory.
We loose if: Q = p * q or Q = p2, where p and q are prime.
It is quite obvious that it is always possible to move in bad position in any other case. That means all other numbers grants us the victory.
We only have to check if Q has a divisor of the loose type. We can easily do it in O(sqrt(Q)) time.
151B - Phone Numbers
In this task you were to implement the described selection of the maximum elements.
151A - Soft Drinking
Soda will be enough for gas = (K * L) / (N * l) toasts.
Limes will last for laim = (C * D) / N toasts.
Salt is enough for sol = P / (p * N) toasts.
Total result: res = min(gas, laim, sol).











For 150B, i think if you give a "k > n case" in the sample , it will reduce lots of misunderstanding.
Can someone give a more detailed explanation for 150B in the cases when k%2=0 and k%2=1.Its not clear for me
Before we check whether k is odd or even(k%2 == 1 or k%2 == 0), we check following two conditions.
k = 1 or к > n, the answer is mn. k = n, the answer is m(n + 1) / 2.
So we know the current k is 0 < k < n
Let's look at the case when k%2 == 1 Let a = an arbitrary character from "m" possible characters. b = an arbitrary character other than "a" from "m" possible characters
If k is odd, a substring whose length is k out of following string is always a palindrome. String : abababababa Substring k=3 => aba or bab k=5 => ababa or babab ... you see the pattern. So we have (m * (m-1)) possible patterns. Now, also remember that a string consisting of same characters are also allowed. string : aaaaaaa substring k=3 =>aaa k=5 => aaaaa And we have "m" number of such strings.
So answer is m*(m-1) + m = m*(m-1+1) = m*m
Let's see what happens when k is even. If k is even, only allowed strings are the ones that consist of same characters. There are m such strings. So answer for (k%2 == 0) is m
Thanks for the explanation :)
I actually failed 150B because of case k > n, and I still don't understand why it is regard the same as k == 1.
case where k == 1 is trivial. The answer is all possible strings.
However, in case k > n, I think the answer should be 0 because you cannot make a SUBSTRING whose length is LONGER than the ORIGINAL string. Also, by definition, a substring is a part of a string, not extended version of a string.
Let's take an example. Let's say n == 5 and k == 7. You have strings made out of "m" selection of characters, and the strings' lengths are always 5. How can you possibly make a substring whose length is 7 from one of strings whose length is 5?
If I am wrong, please help me understand why all possible strings are regarded as palindrome when k > n.
All 0 k-substrings of any string is palindromes.
So any string is correct.
What do you mean by "0 k-substrings of any stirng" ?
Could you please explain with a litte bit more detail?
There are 0 substrings of length
k.All of them are palindromes because Any statement about empty set is truth
Thx.I get it now. :-)
http://en.wikipedia.org/wiki/Vacuous_truth
Let's solve your example (n = 5, k = 7) step by step. Let's check every possible string (let m be 2) if it satisfies the condition.
Let's look on string abaab. Condition is that every substring of length 7 of string abaab is palindrome. Set of such substrings S is empty, it's obvious. So the condition "every element x of S is palindrome" is true.
If you still don't believe me, let's look another way. If condition of type "every element a in set B satisfies condition C" is false, that means, that exists some element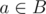 that don't satisfy condition C. In out example, if string abaab doesn't satisfy our condition, then there exist some substring x of our string, that x isn't palindrome. But you can't choose such x: there is no substring of length 7 in our string. So the proposition of that abaab doesn't satisfy condition is false. So this condition is true for abaab, so we have to include abaab to answer.
that don't satisfy condition C. In out example, if string abaab doesn't satisfy our condition, then there exist some substring x of our string, that x isn't palindrome. But you can't choose such x: there is no substring of length 7 in our string. So the proposition of that abaab doesn't satisfy condition is false. So this condition is true for abaab, so we have to include abaab to answer.
Such proof is correct for every string of length n on m-alhpabet, so answer is mn.
i like these problems, but that editorial for 151B is sort of ...
Hi everyone. For 150C can anyone explain details of the point 1 and 2 of this problem?
First lets use the linearity of expected value and solve task independently for each passanger.
For each path segment (route between neighboring stations) we calculate expected value of profit in case we do not sell a ticket for this segment. In case we sell it the expectation of profit is 0.
Can someone help me out with the graph approach of problem 150B, the other approach is straight forward but I can't wrap my head around the graph one, thanks!!
Refer to this link, its a similar problem. https://discuss.codechef.com/t/magical-strings-editorial/11926
Thanks sir ! Your Comments Really Help me alot
thank you GOD ..........your comment helped whole coder community alot
The markdown seems to be broken.
211135796
Div2 D, here is the first solution based on DSU.
what is Div2B , the logic is easy enough but it took me more than an hour just to get the output format right.