I am sorry for mistakes in English and I will be glad if you tell me about them.
168A - Wizards and Demonstration Аuthor PavelKunyavskiy.
In this task, it was necessary to write exactly what has been described in statement. In particular, it was necessary to have 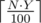 people, who come to the meeting. For this it was necessary to create
people, who come to the meeting. For this it was necessary to create 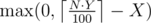 clones.
clones.
168B - Wizards and Minimal Spell Аuthor PavelKunyavskiy.
In this problem you had to write exactly what has been described in statment too. Read lines one by one. Also keep the last block of lines that are not amplyfying. If the next line is amplyfying (which can be checked by linear search), we print the last block, if any, and the line itself. Otherwise, remove all spaces from the string and add to the last block. It only remains to distinguish between an empty block and a block of empty lines.
167A - Wizards and Trolleybuses Аuthor Alex-Gran.
This was the first problem where you had a little bit away from translating statements to a programming language. Because acceleration trolleybuses are all the same and they can slow down immediately, the answer for the next trolleybus is the maximum of the time when it would come if it were not to stop when he reach the rest trolleybuses which was traveling in front of him and the arrival time of the previous trolleybus.
It remains only to calculate the arrival time of each trolleybus if ignore others. Here, the easiest way to analyze two cases. If 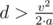 , then trolley should accelerate as long as it can and the answer is equal to
, then trolley should accelerate as long as it can and the answer is equal to 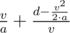 . Otherwise the trolley should accelerate all the time and the answer is equal to
. Otherwise the trolley should accelerate all the time and the answer is equal to 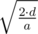 .
.
167B - Wizards and Huge Prize Author PavelKunyavskiy.
This problem can be solved using dynamic programming.
Let d[i][j][m] — the probability we won j of first i days and get bags total capacity of m. For convenience, we assume that the bag is also a prize and the prize is a bag of capacity 0. To do that, retaining a task we must add 1 to all a[i]. Then from d[i][j][m] we can go to the d[i+1][j+1][m+a[i]] with probability p[i]/100, and to d[i+1][j][m] with probability 1-p[i]/100. The answer will be the sum of d[n+1][j][m] for all j,m such that L ≤ j ≤ m + k. This solution works for 2004, and do not fit into the time limit.
It remains to note that if we have over 200 places for prizes, it does not matter how many exactly. So we need to calculate states with m ≤ 200 and now solution works for 2003.
167C - Wizards and Numbers Author Alex-Gran.
Consider the position (a, b). Let a < b. From this there is a move to 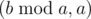 . Recursively check if this position is a winning or a losing. If it is losing, then (a, b) exactly winning. Otherwise, no one will take the remainder. So everyone will subtract from larger number nonnegative degree of smaller. Then the left to learn to solve such problem. You can subtract the nonnegative powers of a from x, and player who cannot move losses. And solve it for
. Recursively check if this position is a winning or a losing. If it is losing, then (a, b) exactly winning. Otherwise, no one will take the remainder. So everyone will subtract from larger number nonnegative degree of smaller. Then the left to learn to solve such problem. You can subtract the nonnegative powers of a from x, and player who cannot move losses. And solve it for 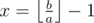 . This problem can be solved as follows. If a is odd, then all odd number are wining. In other all the numbers, giving an odd residue modulo a+1 or -1 residue on the same module are wining. This can be easily proved by induction.
. This problem can be solved as follows. If a is odd, then all odd number are wining. In other all the numbers, giving an odd residue modulo a+1 or -1 residue on the same module are wining. This can be easily proved by induction.
167D - Wizards and Roads Author PavelKunyavskiy.
This was the first really hard problem in the contest. One of the challenges was to understand the statement. I hope that we had written the statement as clear as it possible in this problem.
Consider this graph. In particular, we consider more closely the point with the largest y.
1) It is connected with the highest points on the left and right of it.
2) It is not connected to all other points.
3) It is inside all corners on points from different sides of it.
All three of these properties are seen quite clearly in the pictures.
So,
1) Building roads on the left and right sides are independent.
2) The graph is a tree.
Once a graph is a tree, the maximum matching in it can be found greedy, or with a simple dynamic. But it works in linear time, which clearly is not enough to answer all of 105 queries.
But this is not just a tree! Those who know what it is probably already noticed, that it is Cartesian tree (also known as treep). This allows to get a tree for the subsegments in time which is O(h), counting all the necessary dynamics, where h is the height of the tree.
Well, since the city built at random points (the method for the construction of cities guarantees this), the height of the tree h = O(K + logN).
167E - Wizards and Bets Author Dmitry_Egorov.
This task was about the pathes from the sources to sinks. For this pathes there was a condition which made them dependent — they should not interfere at vertexes. But in any combinatorics is much easier when everything is independent. So we should try to get rid of the condition of the absence of crossings at the vertices. It is very easy — just forget about it. Lets understand why the answer will not change: Suppose that a certain set of ways in which the two paths intersect. We show that taking into account this way, we at the same time take into account an another with the opposite sign. To do this, change the endings for paths that intersect. The signum of the permutation in this case has changed, so this set of paths is taken into account with the opposite sign and their sum is 0.
How can it helps us? If we fix the permutation, the number of sets of paths that it corresponds well to the product of the number of paths for each pair of corresponding source and sink.
Suppose that from the i-th source in the j-th sink there are cntij paths. This value can be calculated by depth-first-search and simple dynamic.
Then the answer is
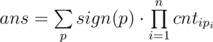
. This value is called the determinant of matrix cnt, which can be calculated using Gauss method in O(S3) time where S is the number of sinks and sources.
And we had to remember about isolated vertexes. Deleting one of them either do not change the answer or multiply the answer by -1.
It remains to see that after deleting all isolated vertexes 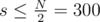 , and 3003 fine fits into TL.
, and 3003 fine fits into TL.











Would you please submit writers' solutions on Codeforces? So we can learn from the code.
In B-DIV-1, Those who missed min(200, now + a[i]) and used now + a[i], and got WA on test-27, minus this post.
Div2 B, Wrong answer on test 20
Checker Log wrong answer Eoln expected, EOF found(line 1575,character 0)
What does it mean?
You need EOLN( i.e "\n"), and maybe text after it, but your answer is ended
Maybe you print less lines than needed
Probably that you are not outputting the last end of line character under some conditions.
Thanks all. Got it.
I used in.hasNext() before. Once I changed it to in.hasNextLine(), it passed.
Not very sure about the difference for this test case.
168A, it was necessary not to forget avoid division by 0, when Y = 0, you should correct the post, because the problem statement says Y >= 1
In Problem B of Div 1, why this case has the right answer of 0.93 not 1.0 ?
1 0 0
7
-1
In my opinion, we can always perform well in 0 round whatever the result of the first tour is, is that correct ? Thanks!
During the contest my opinion is same with yours. But now I understand .In this problem ,the one must play all the tours. then at all , if he won at least l and he can take all prices back home ,it will be consider perfect. So in this case , if he won he can't take the price home so isn't perfect, But if he lost , it will be consider perfect...
Thanks for your comments. However, I still have a silly question. If we only consider perfect win, why the sample input
3 1 0
10 20 30
-1 -1 2
gives 0.3? The only valid way is to lose the first two rounds and win the last one, of which the probability is 0.9 * 0.8 * 0.3 ?In that case last round's award — bag of size 2 compensates first two rounds, so if you win in the last round you can do whatever you want on first two, because now you have bag which can carry all other awards.
Thank you. This makes sense now.
I approached the problem the same way you did — I assumed that I can carry a "huge prize" after a tour win only if I have room in bags for it at that point. I got 0.216 for that case as well.
The worst part is that I tried to fix my code to produce 0.3 still maintaining the same assumption. It took me a while to realize that all it matters is to have enough room in bags after all tours.
Now when I read the statement I am not sure how I misunderstood it, but a lot of other people did — maybe the explanation of the sample should have been a bit more verbose.
Exactly! I always think that I should be able to take all the prize home right after each round... Thank you!
Can somebody throw more light on solution for 167C - Волшебники и числа as to how one obtains the relation to solve the subproblem of subtracting a non-negative degree of smaller number from the larger one?
Let's say the larger number is B, the smaller one is A. If A is odd, the case is pretty simple -- after each turn B % 2 changes, so we win if and only if B%2 = 0.
If A is even, we win if B % (A+1) is even. To prove it we need to prove that each winning state has a move to a losing state, and that any move from the losing state only goes to a winning state.
If B % (A+1) is even, we can always make it odd by subtracting one, if B % (A+1) is not zero, or by subtracting A, if it is zero. That proves that from every winning state there's a move into a losing state.
If B % (A+1) is odd, any turn will make it odd. This can be proven by induction: If you subtract A^0=1, B % (A+1) will obviously become even. Let's say we have proven that subtracting A^k changes oddness. Since subtracting A^k * (A+1) obviously doesn't change oddness (since it is divisible by A+1), subtracting A^(k+1) = A^k * (A+1) — A^k does change it. That proves that from any losing state you can only move to a winning state.
Thanks,I got that..,but I am still confused as the two moves(b->bmoda && b-a^k) are being taken independently to solve the problem.I mean after changing b->bmoda one can take b->b-a^k so why is that not being considered?
Actually you can prove that every turn B % (A+1) must change odd/even, because you can only take A^k for some k>=0, and it is A^k = (A+1 -1)^k = p*(A+1) + (-1)^k which is +1 or -1 when mod (A+1). In the end it is zero, so you win iff B % (A+1) is even. See rng_58's solution.
+/-1 in general doesn't change odd/even for B%(A+1), if A is even. If B%(A+1) = 0, then (B-1)%(A+1) = A -- oddness doesn't change.
thanks for pointing the error. The statement should read: let m = B % (A+1) if m is even, then there is a move that will make it to odd else m is odd, then every move will make it even
Proof: If m is even, then either m=0 or m>0 for m=0, we can take a move of A, then m become B-A = 1 mod (A+1) it is odd for m>0, we can take a move of 1, then m become B-1 = even-1 = odd mod (A+1)
If m is odd, then any move is of the form A^k = (A+1 -1)^k = (-1)^k mod (A+1) So after the move m become odd — (-1)^k = even mod (A+1)
If %(a+1),I can get accepted but what's wrong with %(a-1) (a-1>1) ? It get wa when test b=449843221913123719 a=16 (test 3)
Let's define function F[x]={0,1}: when stat x can make first win F[x]=0,else F[x]=1;
if F[x]=0,there must be a k (k>=0&&b-a^k>=0) makes F[x-a^k]=1;
if F[x]=1,for all k (k>=0&&b-a^k>=0) F[x-a^k]=0;
When F[x]=(x%(a-1))&1.
if F[x]=0. x%(a-1) must be a even,and for all k:
(x-a^k)%(a-1) =x%(a-1) — (a^k)%(a-1) =even + odd= odd
if F[x]=1. x%(a-1) must be a odd,and for all k:
(x-a^k)%(a-1) =x%(a-1) — (a^k)%(a-1) =odd + odd= even
so F[x]=(x%(a-1))&1 satisfy two condition above. What's wrong with this function? Please tell me ,Thx!
(double post)
in 168b, if the input is
#
#
how should the output is ? i think the right is :
#
#
but my code generate:
#
#
and it's accepted (even if tested after the contest), because that kind of test case is not appear,
the test case itself is just 11, if possible, add hacking after contest too
sry for my bad english
I'll tell you big secret: we can't see difference between your three test datas.
i mean, if the input is #(two new line)#, the output in my mind is supposedly #(two new line)#, but my code generate #(one new line)# and accepted
what is the right answer for that ? thx for the reply
From the problem statement: Note that empty lines must be processed just like all the others: they must be joined to the adjacent non-amplifying lines, or preserved in the output, if they are surrounded with amplifying lines on both sides (i.e. the line above it, if there is one, is amplifying, and the line below it, if there is one, is amplifying too).
So, two consecutive empty lines should be joined into one.
Why answer for the first test is 0.3 ?
3 1 0
10 20 30
-1 -1 2
we need to lose first two days (the probabily of this event is 0.9 * 0.8) and win 3 day so finish probability is 0.9 * 0.8 * 0.3
and in pretests 5 we have
1 0 0
7
-1
so the probability that we lose first day is 0.93 and this is the answer.
I can't understand if we don't count lose probabily in example test, why we need to count it in pretest 5?
Thanks
You don't have to lose first two games. If you win the third game, you will have a bag big enough to fit any presents from first two days, should you win any.
I can't not understand the problem description because of my poor English... What a easy problem , however, so little people got accepted...
Div2 B..
Thanks!
What's the expected output format of test case 3 for div2 B? My result has 4 lines and 2 characters as described:
newline
# with newline
newline
# with newline
I got a error saying "expected EOLN" but didn't find out any bug myself. Can someone help me?
What you mentioned is not what you are printing to the output. Look at the judgement protocol carefully. The third line has two spaces in the input and you are printing these two spaces in the output as well instead of removing them — you can see that when you mark the lines. So the judge is expecting an EOLN but finds a space instead.
why is my comment written with so big letters ?
You can edit your post. Instead of pasting your code, you could give the link to it (you can retrieve the link by clicking the upper right "#" when you open the code).
Anyway, on Codeforces you can't use the function
system(), just delete it before submitting the code!For some reason, I am not able to see the codes of "168B — Wizards and Minimal Spell". Even I can't see my own code!! I've got "Wrong Answer of Test 1" verdict btw.
Am I the only one facing this problem?
In problem 167B — Wizards and Huge Prize editorial, it says "The answer will be the sum of $$$d[n+1][j][m]$$$ for all $$$j,m$$$ such ...".
I have the question about this: What if there are some $$$d[n + 1][j + 1][m + ...]$$$ that will include $$$d[n + 1][j][m]$$$ (What I means is they are not distinct to each other), so can we just sum all of them so simply like that?.
I learned that: Only if all the events A, B, C, .. are pairwise distinct, $$$P(A + B + C + ...) = P(A) + P(B) + P(C) + ...$$$. So how are all the $$$d[n + 1][j][m]$$$ are pairwise distinct anyway?
Sorry for my bad English, thanks for reading <3 <3.
Anybody can help me :<< ?
Any..body kind in this awesome Codeforces community :< ?
I suspect the reason nobody has answered so far is that nobody has looked at this editorial for about 3 years.
d[n+1][j][m] is the probability that, at the end, you have won exactly j contests, and have exactly m bags. You can't have won both exactly j and exactly k contests unless j and k are equal, and you can't have exactly m1 and exactly m2 bags unless m1 and m2 are equal, so these events are clearly distinct from each other.
Thank you for clarify it out <3 <3. At first, I was thinking $$$d[n + 1][j + 1][m + X]$$$ can include $$$d[n + 1][j][m]$$$ somehow but it turned out to be wrong.
Love you <3 for answering my question.
Can someone please explain the part
For convenience, we assume that the bag is also a prize and the prize is a bag of capacity 0. To do that, retaining a task we must add 1 to all a[i]in div1 B's editorial ?d[i][j][m] is the probability that, you have participated in contests of first 'i' days , you have won exactly j contests, and have exactly m bags. Now this m is the total capacity you gain after all the contests.
So if we assume a prize is a bag, it will not contribute to the overall capacity. Since a[i]=-1, we add one to make it zero and from d[i][j][m] we can go to the d[i+1][j+1][m+a[i]] (capacity remains then same if we win a prize),
Now we are also assuming bag is a prize and going from d[i][j][m] to the d[i+1][j+1][m+a[i]] state meaning, we are increasing j(the number of prizes won) and assigning that extra capacity ( a[i]+ '1' (this one)). to the bag we considered as a prize. Increasing j here means we considered bag as a prize so we increase the bag capacity by one to accommodate the same bag we considered as a prize.
Problem E is as the same as a well-known lemma: Lindström–Gessel–Viennot lemma