645A - Amity Assessment
Idea: yummy
One solution is to just brute force and use DFS to try all the possibilities. Alternatively, note that two puzzles can be changed to each other if and only if the A, B, and C have the same orientation—clockwise or counterclockwise—in the puzzle. A third option, since the number of possibilities is so small, is to simply classify all of the 4! = 24 configurations by hand.
645B - Mischievous Mess Makers
Idea: ksun48
Loosely speaking, we’re trying to reverse the array as much as possible.
Intuitively, the optimal solution seems to be to switch the first and last cow, then the second and second-to-last cow, and so on for k minutes, unless the sequence is reversed already, in which case we are done. But how can we show that these moves give the optimal messiness?
It is clear when 2·k ≥ n - 1 that we can reverse the array with this method.
However, when 2·k < n - 1, there are going to be cows that we must not have not moved a single time. Since in each move we swap at most 2 cows, there must be at least n - 2·k cows that we have not touched, with pi = i. Two untouched cows i and j must have pi < pj, so there must be at least 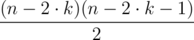 pairs of cows which are ordered correctly.
pairs of cows which are ordered correctly.
In fact, if we follow the above process, we get that pi = (n + 1) - i for the first k and last k cows, while pi = i for the middle n - 2·k cows. From this we can see that the both i < j and pi < pj happen only when i and j are in the middle n - 2·k cows. Therefore we know our algorithm is optimal.
An O(k) solution, therefore, is to count how many incorrectly ordered pairs (i, j) are created at each step and add them up. When we swap cow i and (n + 1) - i in step i, this creates 1 + 2·(n - 2i) more pairs. So the answer will be 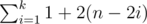 .
.
We can reduce this to O(1) by using our earlier observation, that every pair except those 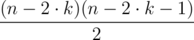 pairs are unordered, which gives
pairs are unordered, which gives 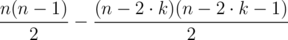 total pairs (i, j). Note that this does always not fit in a 32-bit integer.
total pairs (i, j). Note that this does always not fit in a 32-bit integer.
645C - Enduring Exodus
Idea: GlebsHP
First, observe that the k + 1 rooms that Farmer John books should be consecutive empty rooms. Thus we can loop over all such sets of rooms with a sliding window in linear time. To check the next set of rooms, we simply advance each endpoint of our interval to the next empty room. Every time we do this, we need to compute the optimal placement of Farmer John’s room. We can maintain the position of his room with two pointers—as we slide our window of rooms to the right, the optimal position of Farmer John’s room should always move to the right or remain the same. This solution runs in O(n).
Alternatively, we can use binary search or an STL set to find the best placement for Farmer John’s room as we iterate over the intervals of rooms. The complexity of these approaches is  .
.
645D - Robot Rapping Results Report
Idea: abacadaea
The robots will become fully sorted if and only if there exists a path with n vertices in the directed graph defined by the match results. Because it is guaranteed that the results are not contradictory, this graph must be directed and acyclic—a DAG. Thus we can compute the longest path in this DAG via dynamic programming or a toposort.
We now have two cases. First, if the longest path contains n vertices, then it must uniquely define the ordering of the robots. This means the answer is the time at which the last edge was added to this path. Otherwise, if the longest path has fewer than n vertices, then multiple orderings satisfy the results and you should print - 1. Note that this algorithm runs in O(n + m).
Another solution to this problem binary searches on the answer. For some k, consider only those edges that were added before time k. We can determine if the robots could be totally ordered at time k by running a toposort and checking if the longest path covers all n vertices. This might be more intuitive for some, but has a complexity of  .
.
645E - Intellectual Inquiry
Idea: yummy
For simplicity, let’s represent the letters by 1, 2, ..., k instead of actual characters. Let a[i] denote the number of distinct subsequences of the string that end in the letter i. Appending the letter j to a string only changes the value of a[j]. Note that the new a[j] becomes 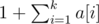 —we can have the single letter j, or append j to any of our old subsequences.
—we can have the single letter j, or append j to any of our old subsequences.
The key observation is that no matter what character j we choose to append, a[j] will always end up the same. This suggests a greedy algorithm—always appending the character j with the smallest a[j]. But how do we know which a[j] is minimal while maintaining their values modulo 109 + 7?
The final observation is that if the last occurrence of j is after the last occurrence of j' in our string, then a[j] > a[j']. This is true because appending j to the string makes a[j] larger than all other a[i]. So instead of choosing the minimum a[i], we can always choose the letter that appeared least recently. Since the sequence of letters we append becomes periodic, our solution runs in 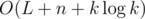 . Of course, we can also find the least recently used letter with less efficient approaches, obtaining solutions with complexity O((L + n)k).
. Of course, we can also find the least recently used letter with less efficient approaches, obtaining solutions with complexity O((L + n)k).
645F - Cowslip Collections
Idea: desert97
After each query, the problem is essentially asking us to compute the sum of 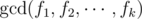 for each choice of k flowers. One quickly notes that it is too slow to loop over all choices of k flowers, as there could be up to
for each choice of k flowers. One quickly notes that it is too slow to loop over all choices of k flowers, as there could be up to 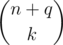 choices of k species.
choices of k species.
So how can we compute a sum over 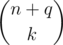 terms? Well, we will definitely need to use the properties of the gcd function. If we figure out for each integer a ≤ 106 how many times
terms? Well, we will definitely need to use the properties of the gcd function. If we figure out for each integer a ≤ 106 how many times 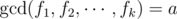 occurs in the sum (let this be g(a)), then our answer will be equal to
occurs in the sum (let this be g(a)), then our answer will be equal to  overall all a.
overall all a.
It seems that if d(a) is the number of multiples of a in our sequence, then there are 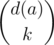 k-tuples which have gcd a. Yet there is something wrong with this reasoning: some of those k-tuples can have gcd 2a, or 3a, or any multiple of a. In fact,
k-tuples which have gcd a. Yet there is something wrong with this reasoning: some of those k-tuples can have gcd 2a, or 3a, or any multiple of a. In fact, 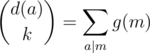 , the number of gcds which are a multiple of a.
, the number of gcds which are a multiple of a.
We will try to write  as a sum of these
as a sum of these 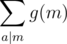 . We’ll take an example, when a ranges from 1 to 4. The sum we wish to compute is g(1) + 2g(2) + 3g(3) + 4g(4) which can be written as
. We’ll take an example, when a ranges from 1 to 4. The sum we wish to compute is g(1) + 2g(2) + 3g(3) + 4g(4) which can be written as
or
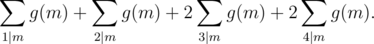
In general, we want to find coefficients pi such that we can write  as
as 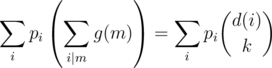 . Equating coefficients of g(a) on both sides, we get that
. Equating coefficients of g(a) on both sides, we get that 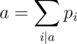 . (The mathematically versed reader will note that pi = φ(i), Euler's totient function, but this is not necessary to solve the problem.)
. (The mathematically versed reader will note that pi = φ(i), Euler's totient function, but this is not necessary to solve the problem.)
We can thus precalculate all pi in  using a recursive formula:
using a recursive formula: 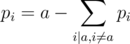 . We can also precalculate
. We can also precalculate 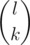 for each l ≤ 200000, so in order to output
for each l ≤ 200000, so in order to output 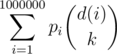 after each query we should keep track of the values of the function d(i), the number of multiples of i. When receiving ci flowers, we only need to update d for the divisors of ci and add
after each query we should keep track of the values of the function d(i), the number of multiples of i. When receiving ci flowers, we only need to update d for the divisors of ci and add 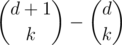 . If we precompute the list of divisors of every integer using a sieve or sqrt checking, each update requires O(divisors).
. If we precompute the list of divisors of every integer using a sieve or sqrt checking, each update requires O(divisors).
Thus the complexity of this algorithm is 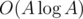 or
or  preprocessing, and O((n + q)·max(divisors)).
preprocessing, and O((n + q)·max(divisors)).
645G - Armistice Area Apportionment
Idea: yummy
Thanks to jqdai0815 and Petr for sharing a solution with me that is much more intuitive than the one I originally had in mind! It works as follows:
First, let’s try to solve the smaller case where we only have two points. Let 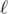 be the line passing through xi and xj. We want to compute the difference of
be the line passing through xi and xj. We want to compute the difference of 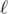 relative to P and Q. Define P’ as the reflection of P over
relative to P and Q. Define P’ as the reflection of P over 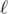 . By the triangle inequality, we have |PX - QX| = |P’X - QX| ≤ P’Q. Equality can be achieved when X, P’ and Q are collinear—that is, when X is the intersection of
. By the triangle inequality, we have |PX - QX| = |P’X - QX| ≤ P’Q. Equality can be achieved when X, P’ and Q are collinear—that is, when X is the intersection of 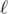 and line P’Q. (If
and line P’Q. (If 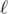 and P’Q are parallel, we can imagine that they intersect at infinity.) Therefore, the difference of a line
and P’Q are parallel, we can imagine that they intersect at infinity.) Therefore, the difference of a line 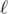 relative to P and Q is the distance from P’ to Q.
relative to P and Q is the distance from P’ to Q.
We can also think about P’ in a different way. Let Ci be the circle with center xi that pases through P. Then P’ is the second intersection of the two circles Ci and Cj. Thus our problem of finding a line with minimum difference becomes equivalent to finding the intersection among {Ci} that lies closest to Q. This last part we can do with a binary search.
Consider the problem of checking if two circles Ci and Cj intersect at a point within a distance r of Q. In other words, we wish to check if they intersect inside a circle S of radius r centered at Q. Let Ai and Aj be the arcs of S contained by Ci and Cj, respectively. Observe that Ci and Cj intersect inside the circle if and only if the two arcs overlap, but do not contain each other. Thus we can verify this condition for all pairs of points with a radial sweep line along the circle. Due to the binary search and the sorting necessary for the sweep line, this solution runs in 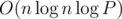 , where P is the precision required.
, where P is the precision required.
One might also wonder if precision will be an issue with all the calculations that we’re doing. It turns out that it won’t be, since our binary search will always stabilize the problem and get us very close to the answer.
Here’s my original solution using a projective transformation:
We begin by binary searching on the the minimum possible difference. Thus we wish to solve the decision problem "Can a difference of k be achieved?" Consider the hyperbola |PX - QX| = k. Note that our answer is affirmative if and only if a pair of outposts defines a line that does not intersect the hyperbola.
Our next step is a reduction to an equivalent decision problem on a circle through a projective transformation. We express this transformation as the composition of two simpler operations. The first is an affine map that takes the hyperbola |PX - QX| = k to the unit hyperbola. The second maps homogenous coordinates (x, y, z) to (z, y, x). Under the latter, the unit hyperbola x2 - y2 = z2 goes to the unit circle x2 + y2 = z2.
Because projective transformations preserve collinearity, a line intersecting the hyperbola is equivalent to a line intersecting the circle. Thus we want to know if any pair of the outposts' images defines a line that does not intersect the circle. We now map the image of each outpost to the minor arc on the unit circle defined by its tangents. (We disregard any points lying inside the circle.) Observe that our condition is equivalent to the existence of two intersecting arcs, neither of which contains the other. Verifying that two such arcs exist can be done with a priority queue and a radial sweep line in  .
.
The total complexity of our solution is therefore  , where P is the precision that we need. It turns out that the implementation of this algorithm is actually pretty neat:
, where P is the precision that we need. It turns out that the implementation of this algorithm is actually pretty neat:










Auto comment: topic has been updated by ksun48 (previous revision, new revision, compare).
Can someone please explain problem C in more detail using the two pointer method (or any other method)?
Assume that the answer is distance X. This means that if farmer john's room is at index i, then there should be at least K free rooms at a distance of X from Farmer John. Which means between index i — X and index i + X there should be atleast K zeroes. Binary search for X and perform an O(N) check to see if such a room exists for Farmer John.
We do the check in O(N) by precomputing the prefixes and suffixes for the '0's in the string.
Code
Initially find the leftmost left and right end point in which there are k+1 empty rooms. Also store the point somewhere near the middle which gives optimum value for this range in O(N) time initially. Next increase the left and right to the next empty room and find the answer using the middle point.If shifting the middle point by to the next room gives optimal answer then shift and update. Do this until right < n.
Auto comment: topic has been updated by ksun48 (previous revision, new revision, compare).
Problem : 655D - Robot Rapping Results Report
LOL, my submission got AC, but my solution(16818709) doesn't work on test:
3 2
1 2
1 3
My output : 2
Right answer : -1
WHAT???? HOW???
...very good tests...
Could someone please explain Problem D's solution using Dynamic Programming. Any help is appreciated. Thank you. :)
You have to find the longest path.
If vertex has no children, longest path, starting from this, is 1 (vertex). Else, look at all children, count longest paths for them, and return 1 + maximum of path lengths among them.
Add some caching. Run this fun for all vertices. Something like this:
I just wasted my 5-6 hours & lost the points in problem D just for this -_- -_- -_-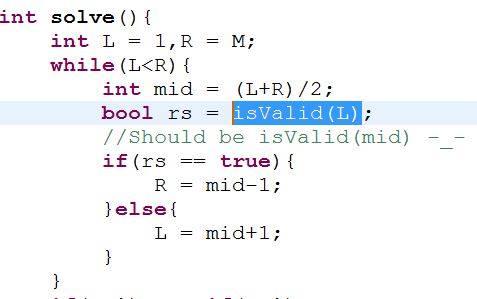
Your binary search looks completely wrong even after the change.
It may seems like that.But after the end of the loop i always handle that properly so that L becomes the actual result. Here is the code. Look at line 140-144.
You wouldn't have to do that if you removed the
-1fromR = mid-1.Can someone please explain why this solution works 16794500 ? It has no return statement in some branch of 'find', but passes tests I'm making for this. It was good I didn't have enough time to try to break it at the contest...
I think what happens is that return value will be passed via EAX register where it essentially will be preserved in chain of returns because no destructors need to be called.
But of course it's undefined behavior, and from practical POV this would likely become broken if there was a local variable of STL container type in the outer scope of this function.
Can someone please explain problem E in more detail(Proof of correctness). Why do we need to choose the letter that appeared least recently ? Any help is appreciated :)
If you look at the dp transition, note that by appending character j, a[j] becomes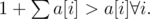 So after appending a letter, its dp state becomes the largest out of every state. Therefore, the later a letter was chosen, the higher its dp state is. So to choose to minimal one, choose the one that appeared earliest!
So after appending a letter, its dp state becomes the largest out of every state. Therefore, the later a letter was chosen, the higher its dp state is. So to choose to minimal one, choose the one that appeared earliest!
I am convinced that picking up the letter that appeared least recently leads us to next optimal state possible from the current state,but how does doing this at each step leads us to global maximum(the maximum possible final answer) ?
Note that the resulting value for a[j] is the same no matter what character j we pick (and all other states stay the same). Therefore, we should be greedy to make the smallest value for a[j] and make it higher.
There is also a little bit simpler way to find last necessary edge in problem D. I found it when checking other coders solutions (kudos to L.Messi EDIT: or rather OhWeOnFire :) ) :
http://codeforces.com/contest/655/submission/16840190
It relies on giving elements ranks (array rnk) during topological sort. rnk[i] means when node i was sorted/positioned in topological sort. So, when you have "end" of a topologically sorted graph like ...->4->10->17 then rnk[17] = 1, rnk[10] = 2, rnk[4] = 3 and so on.
Now all you need to do is go through edges from input and check if, for given edge a->b, rnk[a] == rnk[b] + 1. If so, it means that edge a->b was used to build the longest path. In our example edge 10->17 was used so rnk[10] == rnk[17] + 1. When you get n — 1 of those edges, you've got the whole path.
If anyone interested, my solution based on this idea:
http://codeforces.com/contest/655/submission/16847374
My O(n log n) Java solution is getting TLE on test #13. Has any Java O(n log n) solution passed system tests?
In problem F editorial, I don't understand the below inference. Would be great to get a detailed explanation
http://imgur.com/pOojjiT
The left-hand side counts the number of sets S of size k such that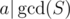 , where
, where 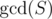 denotes the gcd of elements of the set. This is because, a will divide the gcd of the set if and only if all chosen elements are multiples of a, of which there are d(a) of them.
denotes the gcd of elements of the set. This is because, a will divide the gcd of the set if and only if all chosen elements are multiples of a, of which there are d(a) of them.
The right hand side simply sums over possible gcds that are multiples of a. So they are clearly equal!
Read this.
i don't quite understand the solution of problem F can someone please explain it?
Is there a specific section you are confused about?
Problem F Sorry, but I am not able to understand how are we computing the coefficients pi. ksun48
We need to have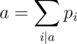 , for all a. These equations are 1 = p1, 2 = p1 + p2, 3 = p1 + p3, 4 = p1 + p2 + p4, etc. We can compute these recursively. To compute pi, since pi = i - p1 - ... - pd, we should start with i and loop through all the divisors of i and subtract the values of p of the divisors.
, for all a. These equations are 1 = p1, 2 = p1 + p2, 3 = p1 + p3, 4 = p1 + p2 + p4, etc. We can compute these recursively. To compute pi, since pi = i - p1 - ... - pd, we should start with i and loop through all the divisors of i and subtract the values of p of the divisors.
Another way to solve problem D by observing that toposort is unique only when there is only one node with indegree 0 at all times. http://codeforces.com/contest/655/submission/18438146
I am not understanding the solution given to problem 645D.We need to finding minimum results needed to get perfect ordering of n vertices,but in editorial he is iterationg through vertices in order and picking up first possible route as minimum .How it is possible??The first possible route may consist of last match result where,if we furthure iterate we may get it in less than previous answer...Please solve my doubt
The earlier edges are added earlier to the adjacency list. So you'll try the better way first.
AMERICA ?
Can anyone tell me why this submission is giving me TLE for D?
In D, we're given that there will be atleast one possible ordering, which means that there can not be any cycles in the graph. Thus the dfs must not be stuck in a loop.
My logic: Since there is an ordering, there must be the smallest element, which has no in-edges, but has only out-edges. We can start our dfs from here. Now we go on until the total number of elements visited is equal to n. We'll save the max index of the edge along with the dfs. So, as soon as we touch the n'th node for the first time, we'll be able to output our answer as the highest seen index of the edge. If n'th node isn't found, then we'll output -1 simply.
I think something is wrong with this, but do not know what exactly. Any help is appreciated!
can we use mobius function in problem F ?