Consider case when we have disjoint polygons on the plane,and they are represented as obstacles,what is the fastest method to calculate distance between 2 point? that's the problem statement...
Let's take variable N and declare it as the total number of vertices on this plane...
I was thinking about some approaches and found this: PATH BETWEEN THESE POINTS GOES ON VERTICES belongs to POLYGONS and GOES ON THIS POINTS ITSELF,that's all... because of that fact I found first approach : make a graph with N+2 points,with expected N^2 edges and run djixstra, complexity of this approach is O(N^2 log N) with memory O(N^2)
But then I realise that it was not enough fast, I started searching and found this material,where(after 11 page in pdf) is described algorithm by [• John Hershberger and Subhash Suri, 1999]: basic idea which works int [time=O(N log N),memory=O(N log N)] time. Here are mentioned dividing plane into 4 part recursively,untill we won't reach single points on plane,like this:
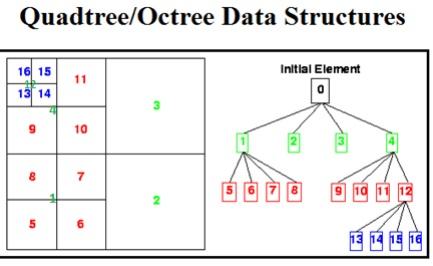
but after that,I didn't get what is explained, if someone has touch/has understood how that algorithm works,please help me to understand how it really works,I want to implement it,thanks in advance :)










