Is it possible to have update query on mo's algorithm ?
In exact I want to know that whether it is possible to solve this problem by using mo's algorithm ?
I am the setter of the problem, but I have used 2d Interval tree to solve the problem. The code is big and quite messy.
Looking for simpler solution. Can anyone help with some clear explanation ?











Why this is not normal segment tree ? Only in first step in parts where numbers is not divisible by 3 you should put 0 instead of that value.
How is this normal segment tree ?
[DELETED]
You need to answer sum of DISTINCT multiples of 3. How would you do it with normal segment tree?
Since Mo's method shuffles the query for speedup, it's intuitively impossible to to solve problems with update. (maybe some fancy method can deal it, but idk)
what will be simpler solution than 2D interval tree ?
i don't know..
I solved using SQRT-DECOMPOSITION + BIT I know there is simillar problem: SPOJ
how to use SQRT decomposition ? I wrote a solution based on SQRTN decomposition, but it took so much time. :(
Why using BIT ? I mean for what type of query ?
Can you help with this problem? Please, tell me idea or give code.
Mo's algorithm is able to solve problems with update too.
Set sizes of blocks to n2 / 3.
So queries [li, ri] can be grouped into at most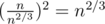 blocks.
blocks.
For each block, deal with query operations which belong to this block and all update operations.
Total complexity is O(n5 / 3).
Can you please explain this in some more detail? If there are some 1e5 operations (including queries and updates), and for each of them, l=1 and r=n? (So all queries belong to same block) I did not understand what you meant by "deal with query operations which belong to this block". The final complexity you mentioned is based on handling each block in O(n) time (please correct me if I'm wrong). How do we do that?
Complexity of dealing with an operation is O(n2 / 3).
You may check out this post: Mo's Algorithm.
how is no. of blocks equal to n^2/3 when size of each block is n^2/3. Also how do you update. Can you please elaborate your explanation. It is not that helpful for beginners.
We group queries based on both endpoints Li and Ri.
Both Li and Ri can belong to one of n1 / 3 blocks.
So queries can belong to one of (n1 / 3)2 = n2 / 3 blocks.
And then how do you perform the query? I have got l and r and I want to update all elements between l and r on which update operation was made and count no. of distinct multiples of 3 between l and r. How to do that? Mo's just sorts queries based on blocks in which l is there, but you want to sort queries based on which block both l and r are situated?
You don't need sort queries.
You may just deal with queries that both L and R belong to same block respectively together.
Ok, I don't sort it. But still how to do update and find answer. If my L and R both belong to same block (which is of size n^2/3) then and if they do not belong to same block then what to do? Also how is this similar to Mo's algorithm?
I mean let's deal with queries Li, Ri that all Li belong to block x and all Ri belong to block y together(Not x=y).
Then it's almost same with Mo's algorithm with no updates.
Ok. So you are processing all queries together such that L is in block x and R is in block y. Now how do you find the answer for some L to R, given that you also have update queries to be performed? And what benefit are we gaining by processing all queries which belong to same block together?
Imagine the naive approach. To process a query [l..r] you'd add all the values V[l..r] in a set and count its size. Now, in order to optimize that, we have grouped queries that are close together, such that when going from a query to a closer one we have fewer insertions / deletions in the set.
It's similar to Mo's Algorithm in the sense that you solve the queries such as to minimize the distance between two adjacent ones (measured in terms of insertions/deletions). It's different from Mo's because it does not need the queries to be solved in some order. Only in more (N2 / 3, to be exact) passes of the queries.
It's kind of fascinating, to be fair.
Could you please elaborate further on your idea? All your comments seem to be very short and I find it hard to understand it. Perhaps if you could provide a practical example such as a problem you have solved using this method and the code, then we would be able to understand the solution much better. What do you do after you create these blocks? How do you support the update queries when they have to be processed chronologically?
What I have understood from above comments (I myself have not used it, so correct me if I am wrong somewhere): I think it is a modified form of Sqrt Decomposition:
Break the array into blocks of size n2 / 3, so you have n1 / 3 blocks.
Consider a subarray starting at the start of block x and ending at the end of block y. We can precompute such answer for all subarrays such that 0 <= x <= y < n1 / 3. So if we can compute answer for a subarray in linear time, this will take O(n * n2 / 3) -> O(n5 / 3) time.
For each update occuring at pos, update the precomputed answer for all subarray's in which pos lies. If we can update in O(1) time for a subarray, this will take O(n2 / 3) time per update.
For query L,R: find the largest precomputed subarray which lies completely inside L,R, and update answer for all remaining elements, which will be O(n2 / 3) in worst case.
All operations have become similar to Mo's algorithm's "add" and "delete" operations. We have O(n5 / 3) precomputation, and O(n2 / 3) per query and update, provided we can update answer for changing one element in a subarray in O(1) time.
In the 4th step, how exactly do you compute the query in O(n^2/3). I don't get that step. I mean,how do you calculate distinct element query in that time?
A problem: Candy Park
And accepted submissions here.
Brief description:
You're given a tree with n nodes.
There is candies on each node. Node i supplies candies of kind c_i only.
We know the value of the ith kind candy is v_i.
If a visitor tastes the same kind candy for the ith time, the weight is w_i.
And his happiness will be sum of w_i*v_j over all candies he tasted.
Queries are: given x and y, answer happiness of a visitor if he walks from node x to node y. He will taste candies on each node he passes exactly once.
Updates are: given x, change c_x to y.
http://uoj.ac/submission/61485
This code shows quite well how it actually works, for a moment I thought it was completely different from Mo's. Thanks (:
I'm still baffled as to why they had to throw the extra "divisible by 3" restriction to the problem...
Hi Everyone!
I made a video editorial on Mo's algorithm with updates. Here is the link:
https://youtu.be/gUpfwVRXhNY
It talks about how we can sort the queries offline with an example and time complexity analysis.
Feel free to ping me in (the very likely) case that you have doubts or suggestions.
Cheers!
Great Work.. Looking for the next video...
my favourite algorithm.