Contest discussion
Problem A. Noldbach problem
To solve this problem you were to find prime numbers in range [2..N]. The constraints were pretty small, so you could do that in any way - using the Sieve of Eratosthenes or simply looping over all possible divisors of a number.
Take every pair of neighboring prime numbers and check if their sum increased by 1 is a prime number too. Count the number of these pairs, compare it to K and output the result.
Problem B. Hierarchy
Note that if employee, except one, has exactly one supervisor, then our hierarchy will be tree-like for sure.
For each employee consider all applications in which he appears as a subordinate. If for more than one employee there are no such applications at all, it's obvious that - 1 is the answer. In other case, for each employee find such an application with minimal cost and add these costs to get the answer.
Alternatively, you could use Kruskal's algorithm finding a minimum spanning tree for a graph. But you should be careful so that you don't assign the second supervisor to some employee.
And yes, the employees' qualifications weren't actually needed to solve this problem :)
Problem C. Balance
Consider the input string A of length n. Let's perform some operations from the problem statement on this string; suppose we obtained some string B. Let compression of string X be a string X' obtained from X by replacing all consecutive equal letters with one such letter. For example, if S = "aabcccbbaa", then its compression S' = "abcba".
Now, consider compressions of strings A and B - A' and B'. It can be proven that if B can be obtained from some string A using some number of operations from the problem statement, then B' is a subsequence of A', and vice versa - if for any strings A and B of equal length B' is a subsequence of A', then string B can be obtained from string A using some number of operations.
Intuitively you can understand it in this manner: suppose we use some letter a from position i of A in order to put letter a at positions j..k of B (again, using problem statement operations). Then we can't use letters at positions 1..i - 1 of string A in order to influence positions k + 1..n of string B in any way; also, we can't use letters at positions i + 1..n of string A in order to influence positions 1..j - 1 of string B.
Now we have some basis for our solution, which will use dynamic programming. We'll form string B letter by letter, considering the fact that B' should still be a subsequence of A' (that is, we'll search for B' in A' while forming B). For this matter we'll keep some position i in string A' denoting where we stopped searching B' in A' at the moment, and three variables kA, kB, kC, denoting the frequences of characters a, b, c respectively in string B. Here are the transitions of our DP:
1) The next character of string B is a. Then we may go from the state (i, kA, kB, kC) to the state (nexti, 'a', kA + 1, kB, kC).
2) The next character of string B is b. Then we may go from the state (i, kA, kB, kC) to the state (nexti, 'b', kA, kB + 1, kC).
3) The next character of string B is c. Then we may go from the state (i, kA, kB, kC) to the state (nexti, 'c', kA, kB, kC + 1).
Where nexti, x is equal to minimal j such that j ≥ i and A'j = x (that is, the nearest occurrence of character x in A', starting from position i). Clearly, if in some case nexti, x is undefined, then the corresponding transition is impossible.
Having calculated f(i, kA, kB, kC), it's easy to find the answer: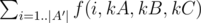 for all triples kA, kB, kC for which the balance condition is fulfilled.
for all triples kA, kB, kC for which the balance condition is fulfilled.
Such a solution exceeds time and memory limits. Note that if string B is going to be balanced, then kA, kB, kC ≤ (n + 2) / 3, so the number of states can be reduced up to 27 times. But it's also possible to decrease memory usage much storing matrix f by layers, where each layer is given by some value of kA (or kB or kC). It's possible since the value of kA is increased either by 0 or by 1 in each transition.
The overall complexity is O(N4) with a quite small constant.
Problem D. Notepad
The answer to the problem is bn - 1 * (b - 1) mod c. The main thing you should be able to do in this problem - count the value of AB mod C for some long numbers A and B and a short number C. Simple exponentiation by squaring exceeds time limit since to converse of B to binary you need about O(|B|2) operations, where |B| is the number of digits in decimal representation of number B.
The first thing to do is to transform A to A mod C. It isn't difficult to understand that this transformation doesn't change the answer.
Let's represent C as C = p1k1p2k2...pmkm, where pi are different prime numbers.
Calculate ti = AB mod piki for all i in the following way. There are two possible cases:
1) A is not divisible by pi: then A and pi are coprime, and you can use Euler's theorem: AB' = AB (mod C), where B' = B mod φ(C) and φ(C) is Euler's totient function;
2) A is divisible by pi: then if B ≥ ki then ti = AB mod piki = 0, and if B < ki then you can calculate ti in any way since B is very small.
Since all piki are pairwise coprime you may use chinese remainder theorem to obtain the answer.
You can also use Euler's theorem directly. Note that if for some B1, B2 ≥ 29 you know that |B1 - B2| mod φ(C) = 0, then all ti for them will be the same (29 is the maximal possible value of ki). Using that you may reduce B so that it becomes relatively small and obtain the answer using exponentiation by squaring.
There is another solution used by many contestants. Represent B as B = d0 + 10d1 + 102d2 + ... + 10mdm, where 0 ≤ di ≤ 9 (in fact di is the i-th digit of B counting from the last). Since ax + y = ax· ay, you know that AB = Ad0· A10d1· ...· A10mdm. The values of ui = A10i can be obtained by successive exponentiation (that is, ui = ui - 110); if you have A10i, it's easy to get A10idi = uidi. The answer is the product above (modulo C, of course).
Problem E. Palisection
The first thing to do is to find all subpalindromes in the given string. For this you may use a beautiful algorithm described for example here. In short, this algorithm find the maximal length of a subpalindrome with its center either at position i of the string or between positions i and i + 1 for each possible placement of the center.
For example, suppose that the maximal subpalindrome length with center at position i is 5; it means that there are three subpalindromes with center at i, with lengths 1 (i..i), 3 (i - 1..i + 1) and 5 (i - 2..i + 2). In general, all starting and finishing positions of subpalindromes with a fixed center lie on some interval of positions, which is pretty easy to find.
Let's find for each position i the value of starti, which is equal to the number of subpalindromes starting at position i. All these values can be found in linear time. Let's create an auxiliary array ai. If after processing a position in the string some new pack of subpalindromes was found and they start at positions i..j, then increase the value of ai by 1, and decrease the value of aj + 1 by 1. Now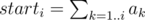 . Proving this fact is left as an exercise to the reader :)
. Proving this fact is left as an exercise to the reader :)
In a similar way it's possible to calculate finishi, which is equal to the number of subpalindromes finishing at position i.
Since it's easy to count the total number of subpalindromes, let's find the number of non-intersecting pairs of subpalindromes and subtract this number from the total number of pairs to obtain the answer. Note that if two subpalindromes don't intersect then one of them lies strictly to the left of the other one in the string. Then, the number of non-intersecting pairs of subpalindromes is equal to: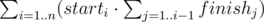
This can be calculated in linear time if the value of is recalculated by addition of finishi before moving from position i to position i + 1.
is recalculated by addition of finishi before moving from position i to position i + 1.
The overall complexity of the algorithm is O(N).
Problem A. Noldbach problem
To solve this problem you were to find prime numbers in range [2..N]. The constraints were pretty small, so you could do that in any way - using the Sieve of Eratosthenes or simply looping over all possible divisors of a number.
Take every pair of neighboring prime numbers and check if their sum increased by 1 is a prime number too. Count the number of these pairs, compare it to K and output the result.
Problem B. Hierarchy
Note that if employee, except one, has exactly one supervisor, then our hierarchy will be tree-like for sure.
For each employee consider all applications in which he appears as a subordinate. If for more than one employee there are no such applications at all, it's obvious that - 1 is the answer. In other case, for each employee find such an application with minimal cost and add these costs to get the answer.
Alternatively, you could use Kruskal's algorithm finding a minimum spanning tree for a graph. But you should be careful so that you don't assign the second supervisor to some employee.
And yes, the employees' qualifications weren't actually needed to solve this problem :)
Problem C. Balance
Consider the input string A of length n. Let's perform some operations from the problem statement on this string; suppose we obtained some string B. Let compression of string X be a string X' obtained from X by replacing all consecutive equal letters with one such letter. For example, if S = "aabcccbbaa", then its compression S' = "abcba".
Now, consider compressions of strings A and B - A' and B'. It can be proven that if B can be obtained from some string A using some number of operations from the problem statement, then B' is a subsequence of A', and vice versa - if for any strings A and B of equal length B' is a subsequence of A', then string B can be obtained from string A using some number of operations.
Intuitively you can understand it in this manner: suppose we use some letter a from position i of A in order to put letter a at positions j..k of B (again, using problem statement operations). Then we can't use letters at positions 1..i - 1 of string A in order to influence positions k + 1..n of string B in any way; also, we can't use letters at positions i + 1..n of string A in order to influence positions 1..j - 1 of string B.
Now we have some basis for our solution, which will use dynamic programming. We'll form string B letter by letter, considering the fact that B' should still be a subsequence of A' (that is, we'll search for B' in A' while forming B). For this matter we'll keep some position i in string A' denoting where we stopped searching B' in A' at the moment, and three variables kA, kB, kC, denoting the frequences of characters a, b, c respectively in string B. Here are the transitions of our DP:
1) The next character of string B is a. Then we may go from the state (i, kA, kB, kC) to the state (nexti, 'a', kA + 1, kB, kC).
2) The next character of string B is b. Then we may go from the state (i, kA, kB, kC) to the state (nexti, 'b', kA, kB + 1, kC).
3) The next character of string B is c. Then we may go from the state (i, kA, kB, kC) to the state (nexti, 'c', kA, kB, kC + 1).
Where nexti, x is equal to minimal j such that j ≥ i and A'j = x (that is, the nearest occurrence of character x in A', starting from position i). Clearly, if in some case nexti, x is undefined, then the corresponding transition is impossible.
Having calculated f(i, kA, kB, kC), it's easy to find the answer:
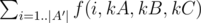 for all triples kA, kB, kC for which the balance condition is fulfilled.
for all triples kA, kB, kC for which the balance condition is fulfilled.Such a solution exceeds time and memory limits. Note that if string B is going to be balanced, then kA, kB, kC ≤ (n + 2) / 3, so the number of states can be reduced up to 27 times. But it's also possible to decrease memory usage much storing matrix f by layers, where each layer is given by some value of kA (or kB or kC). It's possible since the value of kA is increased either by 0 or by 1 in each transition.
The overall complexity is O(N4) with a quite small constant.
Problem D. Notepad
The answer to the problem is bn - 1 * (b - 1) mod c. The main thing you should be able to do in this problem - count the value of AB mod C for some long numbers A and B and a short number C. Simple exponentiation by squaring exceeds time limit since to converse of B to binary you need about O(|B|2) operations, where |B| is the number of digits in decimal representation of number B.
The first thing to do is to transform A to A mod C. It isn't difficult to understand that this transformation doesn't change the answer.
Let's represent C as C = p1k1p2k2...pmkm, where pi are different prime numbers.
Calculate ti = AB mod piki for all i in the following way. There are two possible cases:
1) A is not divisible by pi: then A and pi are coprime, and you can use Euler's theorem: AB' = AB (mod C), where B' = B mod φ(C) and φ(C) is Euler's totient function;
2) A is divisible by pi: then if B ≥ ki then ti = AB mod piki = 0, and if B < ki then you can calculate ti in any way since B is very small.
Since all piki are pairwise coprime you may use chinese remainder theorem to obtain the answer.
You can also use Euler's theorem directly. Note that if for some B1, B2 ≥ 29 you know that |B1 - B2| mod φ(C) = 0, then all ti for them will be the same (29 is the maximal possible value of ki). Using that you may reduce B so that it becomes relatively small and obtain the answer using exponentiation by squaring.
There is another solution used by many contestants. Represent B as B = d0 + 10d1 + 102d2 + ... + 10mdm, where 0 ≤ di ≤ 9 (in fact di is the i-th digit of B counting from the last). Since ax + y = ax· ay, you know that AB = Ad0· A10d1· ...· A10mdm. The values of ui = A10i can be obtained by successive exponentiation (that is, ui = ui - 110); if you have A10i, it's easy to get A10idi = uidi. The answer is the product above (modulo C, of course).
Problem E. Palisection
The first thing to do is to find all subpalindromes in the given string. For this you may use a beautiful algorithm described for example here. In short, this algorithm find the maximal length of a subpalindrome with its center either at position i of the string or between positions i and i + 1 for each possible placement of the center.
For example, suppose that the maximal subpalindrome length with center at position i is 5; it means that there are three subpalindromes with center at i, with lengths 1 (i..i), 3 (i - 1..i + 1) and 5 (i - 2..i + 2). In general, all starting and finishing positions of subpalindromes with a fixed center lie on some interval of positions, which is pretty easy to find.
Let's find for each position i the value of starti, which is equal to the number of subpalindromes starting at position i. All these values can be found in linear time. Let's create an auxiliary array ai. If after processing a position in the string some new pack of subpalindromes was found and they start at positions i..j, then increase the value of ai by 1, and decrease the value of aj + 1 by 1. Now
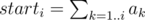 . Proving this fact is left as an exercise to the reader :)
. Proving this fact is left as an exercise to the reader :)In a similar way it's possible to calculate finishi, which is equal to the number of subpalindromes finishing at position i.
Since it's easy to count the total number of subpalindromes, let's find the number of non-intersecting pairs of subpalindromes and subtract this number from the total number of pairs to obtain the answer. Note that if two subpalindromes don't intersect then one of them lies strictly to the left of the other one in the string. Then, the number of non-intersecting pairs of subpalindromes is equal to:
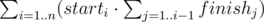
This can be calculated in linear time if the value of
 is recalculated by addition of finishi before moving from position i to position i + 1.
is recalculated by addition of finishi before moving from position i to position i + 1.The overall complexity of the algorithm is O(N).











But what can you say about my solution?
In fact, it looks like:
a %= c;
p = phi(c);
ans = (a ^ (b % p)) % c;
if (b >= p && ((a ^ p) % c) == 0)
ans = 0;
Maybe there is some subtle counter-example?
Ah, of course, my bad memory :)
a %= c;
p = phi(c);
ans = (a ^ (b % p)) % c;
if (b >= p)
ans *= ((a ^ p) % c);
Can anyone explaine why does this solution work?
int[][][][] dp = new int[151][52][][];
for (int i = 0; i < dp.length; ++i) {
for (int j = 0; j < 52; ++j) {
dp[i][j] = new int[52 - j][];
for (int k = 0; j + k < 52; ++j) {
dp[i][j][k] = new int[52 - j - k];
}
}
}
This allocates only the elements actually needed by the solution, so fitting in memory limit.
C/C++ users may use "full" allocation - unused pages of memory will not be loaded, and ML will not be overcomed. But use it with care - there are some problems (not this one) using "lazy" dynamic programming where it is possible to load all or just too many pages by some tricky tests, even if the number of used cells is acceptable.
The tutorial is nice.
Will you post the tutorials for coming contests as well?
Blog not visible tourist
Unable to parse markup [type=CF_HTML]
omg tourist round
=) I can't solve this =)