Click here to download the pdf
Pre Requisites
Binary Search — How it works and where can it be applied!
Motivation Problem
We aim to solve this problem : Meteors
The question simply states :
There are N member states and M sectors. Each sector is owned by a member state. There are Q queries, each of which denote the amount of meteor shower in a [L, R] range of sectors on that day. The ith member state wants to collect reqd[i] meteors over all its sectors. For every member state, what is the minimum number of days it would have to wait to collect atleast the required amount of meteors?
Solution
The naive solution here is to do a binary search for each of the N member states. We can update in a range using segment trees with lazy propagation for each query. The time complexity of such a solution would be O(N * logQ * Q * logM). But this one will easily TLE.
Let's see if there's something we are overdoing. For every member state, the binary search applies all the queries until a point multiple times! For example, the first value of mid in the binary search is same for all member states, but we are unnecessarily applying this update everytime, instead of somehow caching it.
Let's do all of these N binary searches in a slightly different fashion. Suppose, in every step we group member states by the range of their binary search. In the first step, all member states lie in range [1, Q]. In the second step, some lie in range [1, Q / 2] while some lie in range [Q / 2, Q] depending on whether the binary search predicate is satisfied. In the third step, the ranges would be [1, Q / 4], [Q / 4, Q / 2], [Q / 2, 3Q / 4], [3Q / 4, Q]. So after logQ steps, every range is a single point, denoting the answer for that member state. Also, for each step running the simulation of all Q queries once is sufficient since it can cater to all the member states. This is pretty effective as we can get our answer in Q * logQ simulations rather than N * Q * logQ simulations. Since each simulation is effectively O(logM), we can now solve this problem in O(Q * logQ * logM).
"A cool way to visualize this is to think of a binary search tree. Suppose we are doing standard binary search, and we reject the right interval — this can be thought of as moving left in the tree. Similarly, if we reject the left interval, we are moving right in the tree.
So what Parallel Binary Search does is move one step down in N binary search trees simultaneously in one "sweep", taking O(N * X) time, where X is dependent on the problem and the data structures used in it. Since the height of each tree is LogN, the complexity is O(N * X * logN)." — animeshf
Implementation
We would need the following data structures in our implementation :
- linked list for every member state, denoting the sectors he owns.
- arrays L and R denoting range of binary search for each member state.
- range update and query structure for Q queries.
- linked list check for each mid value of current ranges of binary search. For every mid value, store the member states that need to be checked.
The implementation is actually pretty straight forward once you get the idea. For every step in the simulation, we do the following :
- Clear range tree, and update the linked lists for mid values.
- Run every query sequentially and check if the linked list for this query is empty or not. If not, check for the member states in the linked list and update their binary search interval accordingly.
Pseudo Code
for all logQ steps:
clear range tree and linked list check
for all member states i:
if L[i] != R[i]:
mid = (L[i] + R[i]) / 2
insert i in check[mid]
for all queries q:
apply(q)
for all member states m in check[q]:
if m has requirements fulfilled:
R[m] = q
else:
L[m] = q + 1
In this code, the apply() function applies the current update, i.e. , it executes the range update on segment tree. Also to check if the requirements are fulfilled, one needs to traverse over all the sectors owner by that member state and find out the sum. In case you still have doubts, go over to the next section and see my code for this problem.
Problems to try
Conclusion
I heard about this topic pretty recently, but was unable to find any good tutorial. I picked up this trick from some comments on codeforces blog on Meteors problem. Alternate solutions to the mentioned problems are also welcome, almost every question on parallel binary search can also be solved with some persistent data structure, unless there is a memory constraint. Feel free to point out errors, or make this tutorial better in any way!
Happy Coding!











I've heard about Meteors so many times. Thanks to you, today I've finally decided to solve it.
My implementation is slightly different. Maybe it will be easier for some people, so I'll describe it.
I wrote a recursive function
rec(int low, int high, vector<int> owners)and I run it once asrec(1, q, {1,2,...,n}). Vector owners contains people for which answer is in interval [low, high].Let's denote mid = (low + high) / 2. I want to know which owners already won after the first mid queries. Then, I run
rec(low, mid, owners_who_won)andrec(mid, high, those_who_didnt).To check "which owners already won" I need standard range tree. In my code below you can find a variable act_tree denoting the number of first queries summed in the tree. Let's say my function is run with arguments low = 70 and high = 90. My global tree should now contain the sum of first mid = 80 queries (so there should be act_tree = 80). Later I want to run rec(70, 80) and rec(80, 90). I need to do the following:
The time complexity is something like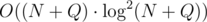 . Naive implementation will result in the memory complexity
. Naive implementation will result in the memory complexity 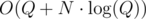 . To make it O(N + Q) you need to pass vector owners by reference and clear it after checking which owners already won. Check details in my code below.
. To make it O(N + Q) you need to pass vector owners by reference and clear it after checking which owners already won. Check details in my code below.
Cool implementation! Btw you managed to pass time limit using recursion and vectors? I found time limit to be pretty strict. Numerous optimizations were required even with BIT to get an AC.
Thanks. Cool blog ;)
Yes. I didn't use BIT and I got AC even without passing vector by reference (so, with memory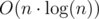 . I think that recursion isn't a problem here because we get
. I think that recursion isn't a problem here because we get 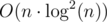 operations in a tree. Without that, recursion is
operations in a tree. Without that, recursion is 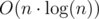 so it can be slower and it shouldn't affect the overall running time. Apparently, my solution may use less tree operations (e.g. two times less) than yours and it's why you had to use BIT. Or maybe for some other special test my solution would be slower, it's hard to say.
so it can be slower and it shouldn't affect the overall running time. Apparently, my solution may use less tree operations (e.g. two times less) than yours and it's why you had to use BIT. Or maybe for some other special test my solution would be slower, it's hard to say.
Hi, I have a question. Why do you set ans[who]=high when "who" can get his desired value in mid point.
Update: clear.
owners.clear(); // thanks to this line the memory is O(n), not O(n log(n))I think without calling
owners.shrink_to_fit()the memory is still O(nlog(n)), right?Yes, you are right. Or we should clear it by swapping with an empty vector
vector<int>().swap(owners);.Hi,
Can you point to some tutorial for the tree you're using ? I tried searching but couldn't find any.
Thanks
It's an iteractive segment tree. For reference: https://codeforces.com/blog/entry/18051
Iteractive segtree and BIT are fast range data structures, so you could use a regular BIT also instead of the segtree without a problem
I was discussing with satyaki3794 about his solution to Travel in Hackerland using parallel binary search. My first reaction when he told me about this technique was "Wow you don't have sequential code ? I have never submitted a parallel code online" :P
My bad. He then pointed me to the METEORS problem.
please update the link for the "Travel-in-hackerland" question :P .
https://www.hackerrank.com/contests/may-world-codesprint/challenges/travel-in-hackerland
Auto comment: topic has been updated by himanshujaju (previous revision, new revision, compare).
SRM 675 Div.1 LimitedMemorySeries1(500pts) can be solved with this method.
This is my code accepted in the practice room. http://ideone.com/Dm2x4M
Div1 500! Wow, I never knew this would be so useful :P
My code is similar to yours, can you point out the error in this please? I am getting wrong answer. Code
In line 77 , you need to break when current sum exceeds requirement , else you will overshoot ll_max.
Great Blog!
A cool way to visualize this is to think of a binary search tree. Suppose we are doing standard binary search, and we reject the right interval — this can be thought of as moving left in the tree. Similarly, if we reject the left interval, we are moving right in the tree.
So what Parallel Binary Search does is move one step down in N binary search trees simultaneously in one "sweep", taking O(N * X) time, where X is dependent on the problem and the data structures used in it. Since the height of each tree is Log N, the complexity is O(N * X * logN)
Just the kind of explanation I was looking for while writing this blog! You don't mind if I add this to the blog, right?
Not at all!
That's a cool trick :)
I tried to solve the problem "Make n00b land great again" but couldn't figure out how to efficiently update the queries. Can you please explain how to do it efficiently?
You can go through it's editorial. Updates can be handled by range tree.
Oh thanks! Didn't see that the editorial was there.
Thanks himanshujaju for a nice blog post. This helped me to learn a new technique :) ..Parallel BS is awesome..Anyway, at first while reading Problem description for METEORS , first thing that come to my mind was Persistence Segment-tree as this is a straightforward and implemented and got AC with 165M memory & 2.82 time, after that implemented ParallelBS (first time, of course :) ) and got AC with 22M & 4.72 time (huge time but less memory ;) ).....Then, after looking RANK for that problem, I wondered how some people managed to solve this problem in less time like 0.34,0.58,0.93...Is there any better approach?
Can you share your approach for the Persistent Segment-tree solution?
I did it with persistent segment tree by performing point-update of +a[i] on l[i] and -a[i] on r[i]+1 (for l[i]<=r[i], similar updates for l[i]>r[i]). But it got TLE without fast-io , and AC with a time of 7.72 s with fast-io.
What we need here in segment-tree is "Range update Point query". It seems to require lazy here, but we may skip lazy by performing something like this: At the time of Range update we have to update the sum for all the segments which encounter while updating that range. And, now at the time of Point query we just have to go down to the point on segment-tree by adding up the sum of segments that encounter while going down to this point...Hope it helps :)
can you share your persistent segment tree solution?
Lazy segment trees are actually not necessary for this problem. You can also do the line sweep technique to count how many meteors have been added to sector i for every i (in which events are endpoints of queries and sectors) to knock down a log off the complexity, making it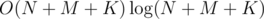 .
.
I couldn't understand your solution. Could you share how your code runs on the sample?
I guess it's a lot closer to Errichto's implementation than the original one:
rec(minq, maxq, events)performs all queries between minq and(minq+maxq)/2and gets the number of meteors for every state.The way it performs the queries is by doing a line sweep:
eventsis a sorted list of the endpoints of all queries in the range[minq, maxq](KTYPE events), and for each starting endpoint I add ai to the current section's meteor count, for each ending endpoint I subtract ai. This way for every sector I know how many meteors it has for those queries.eventsalso contains all states I'm searching in this query range (NTYPE events), and a list of sectors that those states own (MTYPE events).For the first step of the sample I would first call:
rec(minq=0, maxq=3, { states:{0,1,2,3}, sectors:{0,1,2,3,4}, queries:{0,1,2} })(minq+maxq)/2is 1, so I'm running the first two queries and ignoring the rest. The last state succeeds, and the two first states fail, so the recursion splits into:rec(minq=0, maxq=1, { states: {2}, sectors: {1, 4}, queries:{0,1})rec(minq=2, maxq=3, { states: {0,1}, sectors: {0, 2, 3}, queries: {2} }).Because we will never consider queries 0 and 1 for states 0 and 1 anymore, I subtract how many meteors those states had from the required number of meteors before recursing.
The second round of splits will produce:
rec(minq=0, maxq=0, { states: {2}, sectors: {1, 4}, queries:{0})rec(minq=1, maxq=1, { states: {}, sectors: {}, queries:{1})rec(minq=2, maxq=2, { states: {0}, sectors: {0, 3}, queries: {2} }).rec(minq=3, maxq=3, { states: {1}, sectors: {2}, queries: {} }).And we can see that minq indicates the answer for every state in the corresponding list.
i just solved the METEORS question.I was getting wrong answer because of the fact that i was not breaking out of loop when summing the value of all the sectors for a member.I was doing all calculations in long long in c++ . So why does this happen isn't the maximum number is 3*10^14 which long long can handle, on breaking out of loop as soon as my required is satisfied it got AC .Can anyone answer why?
What if all queries is to increase by 109 in the entire range?
A separate but related problem: can we run Q binary searches (e.g. Q lower_bound operations) over a sorted array of N elements faster than in O(Q * logN)? (It is assumed that all Q queries are known beforehand).
You can first sort the Q queries in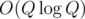 and then iterate over two arrays simultaneously in O(N + Q). So, the complexity is
and then iterate over two arrays simultaneously in O(N + Q). So, the complexity is 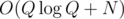 . But... is this complexity better? I don't see any example (like
. But... is this complexity better? I don't see any example (like 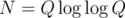 ).
).
A curious case. Assuming the following calculation is correct, the complexity is not better https://www.wolframalpha.com/input/?i=solve+Q%2Alog%28N%29+%3C+Q%2Alog%28Q%29%2BN
It looks like there is no way to improve the case Q=N. Otherwise we could sort faster than N*logN. Or at least we could sort several arrays faster. We could sort one of them in N*logN and others faster then N*logN (by doing parallel binary searches over the first already sorted array).
I tried this logic to prove that it's impossible to solve your problem faster — and I didn't succeed. So, I don't think you're right here. UpperBound isn't enough to sort the other array. For example, consider the first array to be {100,200,300,400,500} and a new array {17,29,18,50,10,30}. Still, maybe some similar proof will be correct.
Let assume the time complexity of that problem with N = Q is T(N). Furthermore, I do some technical assumptions. T(N) ≤ T(2N + a) / 2 for all N, a ≥ 0 and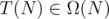 .
.
I show that we can sort an array of N distinct elements in O(T(N)) expected time under the comparison model with randomization.
Because we chose randomly, and we assumed that the each element is distinct, each group (the elements with the same query result) is a constant size. We can thus sort each group in O(1) expected time.
Let the runtime of the algorithm above be S(N). By the assumption on T(·), we can easily see that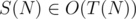 .
.
Because we cannot sort an array in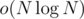 time under the comparison model even with randomization, we conclude that
time under the comparison model even with randomization, we conclude that 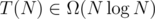 ■.
■.
Open problem: can this reduction be derandomized?
I don't think it's obvious that "each group is a constant size". It's logical/obvious that the sum of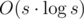 (where s is size of group) is O(n) in total but you didn't prove it. Still, your proof is nice, thanks.
(where s is size of group) is O(n) in total but you didn't prove it. Still, your proof is nice, thanks.
By the way, what is the expected size of the biggest of groups? It sounds like something very hard to analyze. Maybe some tedious calculations would be enough here.
I finally realized what answer to this question I wanted. My initial thought was that when doing Q independent binary searches, we perform redundant work. And indeed there is a way to reduce it, though the worst case complexity will remain O(Q * logN).
We can visualize binary search as a binary search tree traversal. We will do a standard tree traversal, but we'll process all queries together. To achieve this, we sort our queries and start from the root of the tree, which corresponds to the median of the array. By doing binary search on queries we find which queries lie to the left and which lie to the right of the root node. We continue traversing tree recursively. As a result, we reduce the number of comparisons due to partially coinciding search paths.
Hey, can somebody plz help me in debugging my code for meteors. Code
P.S. — I also wrote an input generator and compared my solution to one of the accepted solutions, but could not find any mismatch.
Your bug is at line 104. This sum may be very big, around 10^20.
Thanks a lot. Accepted :)
Selective Additions — A problem from the last Hourrank on Hackerrank. Can be solved using Parallel BS.
cool application.
I think we can do all these questions with Persistent Segment Tree with Lazy Propagation.
Here is my code of Meteors — https://ideone.com/PgJg1E
Complexity — O(M*logQ*logM)
One downside of this is that it takes a lot of memory.
I don't think it is possible to do Lazy Propagation in Persistent Segment Tree. Memory Complexity becomes O(QN), that isn't the purpose of Persistent Segment Tree.
You may get AC in SPOJ, because in SPOJ you have 1.5GB Memory limit, and as I see, your code got AC with 1.3GB memory usages.
But in the main contest of POI, Memory limit was 64MB ;)
Try submitting here — SZKOpul — Meteors
It is possible to do Lazy Propagation in Persistent Segment Tree. The Memory Complexity O(N + Q*logM). You can see in my code that while querying/updating I'm making at max O(logM) nodes only.
Yes, it won't give AC if the memory limit is tight. I had already mentioned the downside.
P.S. I was easily able to reduce the memory to 0.44GB. Just reduced the array size.
Code — https://ideone.com/x7dwqq
I don't think that memory complexity will still be O(N + Q log M), because, when you propagate a lazy value, in the end you may end up creating a tree for that range. So memory complexity is something greater than O(Q log M) and Worst case O(QN).
Please take a look at my code carefully. Try to run it for some cases. You'll know then :)
you don't create a new tree for the range, you just update the node, it's still that memory complexity. If you used QN memory each time it wouldn't make any sense, because that would assume regular lazy propagation would be QN, since you access/create same number of nodes (log n).
Please, update the link for "travel-in hackerland" question,
it's new link is this
How is the brute force complexity the one given above? For each station, we do binary search on queries and we keep 2 pointers, one for binary search and other for the queries pointer which points upto where the queries are applied.I suppose this pointer moves at max the whole queries array twice. So must not it be Q+LogQ instead of Q.LogQ. And then, we apply range query range update using BIT, so what I suppose is the complexity must not contain the factor of Q. Please correct me if I am wrong.
Here's a problem related to the concept.
https://agc002.contest.atcoder.jp/tasks/agc002_d
Here's another problem: Evil Chris
These tasks also solvable using Parallel Binary Search:
Is New Road Queries time limit passable with Parallel Binary Search? I got TLE :(
Yes, I solved it using Parallel Binary Search, it's really similar to Stamp Rally.
Can you explain your idea? or send your code?
Accepted Code: https://cses.fi/paste/bfe897265843ddb05a70d4/
Here's my code https://cses.fi/paste/5bdf60ff032634355c22d8/ Maybe it TLE because I use recursive ?
Edit: Thanks! I learned iterative pbs from your code. It's accepted now :)
I wonder if the "find k-th element in a range with updates" problem can be solved using the author's implementation. I solved it using the recursion style implementation but I don't think the same idea can be applied here?