There is still no formal EDITORIAL for Codeforces Round #364 (Div. 2) yet ,so I write a informal one.
Sorry for my poor English and poor format.
You can calculate the sum (x) of a pair of cards.
x=2*(a1+a2+...+an)/n
For every card ai,find a card ak which ai+ak=x and k is not used.
The n is small,so you can simplely write a o(n*n) solution(also there is a o(n) one,o(n*n) is enough).
My o(n*n) solution:19328905
You can just record the number of rows and columns that is not under attack.
If r rows and c columns is not under attack there is r*c cells that is not under attack.
It's o(m).
My o(m) solution:19330540
You can just use two pointers
There are x types of Pokemon
if [i,dp[i]-1] has x-1 types of Pokemon and [i,dp[i]] has x types of Pokemon
dp[i+1]>=dp[i]
so it's o(n)
my o(xlogx+n) solution:19332828
It's a math problem.
let d=ceil(n/k)
Just look at the bus.
it goes like that:
_>>>>>>>>>>>>
____<<<<<<<<<
____>>>>>>>>>>>>
_______<<<<<<<<<
_______>>>>>>>>>>>>
__________<<<<<<<<<
__________>>>>>>>>>>>>
The '_' means empty(I cannot format it).
The long lengths are the same(x) and goes to right.
The short lengths are the same(y) and goes to left.
It goes to right and put the old students down and does to left and welcome new students.
so x+y:x-y=v2:v1
it goes for d xs and (d-1) ys
so:
1:d*x-(d-1)*y=l
2:x+y:x-y=v2:v1
3:ans=(d*x+(d-1)*y)/v2
so ans=l/v2*((d*2-1)*v2+v1)/(v2+(d*2-1)*v1)
It's o(1).
my o(1) solution:19334768
701E - Connecting Universities
Let's take 1 as the root of the tree.
Record the depth of every vertex(depth of 1 is 0).
Record the number of schools of the subtree of every vertex.
The sum of the depth of the lca of every pair of school should as small as possible.
Consider 2x schools of the subtree of vertex y(may be 2x is not the number of all the schools of the subtree of vertex y)
every depth of lca of the 2x schools is at least the depth of y .
If a subtree of the son of y has k schools in the 2x schools(not in all the schools).
1:if the k of every son is always mink<=x
you can match the schools to make every lca y
2:if for son z,mink>x
match (2x-mink) schools of the subtree of z with the schools not in the subtree of z but in the subtree of y
just look at z like look at y
so,it's o(n)
my o(n) solution:19344918
First,find a way from s to t.
If there is no such way,the answer is 0.
If there is such way,try to stop every edge on it and try to find bridges and upuate the answer.
How to find a bridge?
DFS it with root s,record the depth of every vertex and the least depth it can reach without passing its father.
If the least depth x can reach without passing x's father > the depth of y then (x,y) is a bridge.
Try to stop edges o(n),and finding bridges o(m).
It's o(nm).
My o(nm) solution:19462368
Other solutions are welcomed.
If you find any mistakes,tell me.
UPD1:solution to problem F










Nice blog but try to use some formatting. It's hard to read it that way.
Can you help me with the formatting?
Blog uses markdown with latex. You can use the numbered list and bullet option in the blog. For maths formula write them between "$" symbols and use latex formula (you can refer wikipedia for this). For links and images you can use the link symbol.
BTW nice blog.
Auto comment: topic has been updated by -skyline- (previous revision, new revision, compare).
Auto comment: topic has been updated by -skyline- (previous revision, new revision, compare).
Read this Blog it will teach you how to do the formatting.
Solution for problem F: 1) Lets try to find any simple path from S to T. It has O(n) edges. Of course if there isn't such path the answer is 0. 2) It's obvious that we have to delete at least one of these edges. Lets iterate over these edges and try to delete each of them. 3) Now we have graph where we can delete no more than 1 edge. If now there isn't path from S to T than we just do ans=min(ans, w of edge that we chosen on step 1); If there is path between S and T we can use bridges-finding algo. It works in O(m). It's easy to see that we can delete every bridge to delete the path between S and T. So we just chose the cheapest bridge and do ans=min(ans, w of edge that we chosen on step 1 + w of cheapest bridge); 4) Of course if we didn't find any bridges on any iteration ans is -1, else just cout<<ans. Total we get O(nm)
I solved 701E - Connecting Universities this way:
First, denote V[node] as the number of universities in the subtree whose root is node.
Now, for every edge E(u, v) where v is the child of u, let's count the maximum number of paths between pairs of universities that could traverse this edge:
paths(E(u, v)) = min(V[v], 2 * k - V[v])
The answer is given by the sum of paths for every edge of the tree.
Here is my solution: 19387861
I think your solution to 701C is actually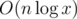 because in the beginning, we access
because in the beginning, we access 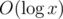 operations for
operations for 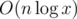 complexity.
complexity.
m[cc]fori=1toi=n, meaning we haveniterations, giving usHowever, if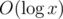 to O(1), which changes the complexity to just O(n).
to O(1), which changes the complexity to just O(n).
map<char, int> mis changed toint m[256], we change the operations in m fromThank you! I was not able to find any idea for E
In D, how did you get x+y : x-y = v2:v1 ?
edit : click
Nice editorial! But I had a doubt. In problem 701D - As Fast As Possible, why are the lengths x and y the same? also why is x+y:x-y = v2:v1? Could you provide a slightly more in depth explanation?
Here's what I think — when the bus drops off the first batch of students, and returns, those students walk the remaining distance at a constant pace (v1). But during that time, the other students must've already started walking from starting point at speed v1. Its important that every student covers equal distances at speeds v1 and v2. Therefore, x should be the same for all, because this is proportional to the time one travels on bus. Now, the moment the bus picks up some students, goes x distance, and turns back, the remaining students keep walking at pace v1 from the point of pick up. Because the students and the bus both travel at constant pace, therefore, when the bus reverses, they meet after the bus travels a distance y, and the students have already moved a distance x-y. Thus y is a constant as seen from the expression
(x-y)/v1=(x+y)/v2as we equate the times the students traverse on foot from the pickup point, till the bus reaches them after dropping off some students, starting from the pickup point. Note that x,v1,v2 are all constants, so y is also a constant.p/v1+(l-p)/v2 should be same for all(total time taken) where p is the distance covered by one student on foot. If p varies from student to student, then, suppose the next student covers p-k distance on foot, then he will cover l-p+k distance by bus.
p/v1 + (l-p)/v2 = (p-k)/v1 + (l-p+k)/v2
This statement is only true for v1=v2.
Thanks! I thought of another explanation but yours is very simple and elegant. The fact that they HAVE to cover the same distance by bus and foot just struck me. I thought of it as "Every time you pick up a student by bus, you have to drop him off at the students ahead of him, so they all reach at the same time.", which also gives you that x is constant.
You're welcome :)
I used Binary Search to Solve D.
You can ask whether it is possible to drop all students within a given time t.
The bus starts and drops all students at distance x such that
x / v2 + (l — x) / v1 = t
and goes back to pick up the remaining students. We can easily calculate the distance where they meet.
Run this simulation for at max 10000 steps.
Solution
Time complexity :- 10000 log(1000000000)
link :- http://codeforces.com/contest/701/submission/19420349
Solved the problem after the contest. Guess the binary search tag affected my algorithm rather than coming up with a much simpler formula :p
701F - Break Up is a beautiful problem for graph lovers out there :D. It can be tedious to code, though.
Kudos to the author(s) :)
Auto comment: topic has been updated by -skyline- (previous revision, new revision, compare).