so yesterday i just learned the union-find data structure, and i found this problem: https://open.kattis.com/problems/almostunionfind
my approach is as following: implement basic union-find, but also add array sum[] for the sum of the group and freq[], the number for elements in the group
i also "made" the group using a vector of vector, so if there is a group {1,3,5} and 1 is the leader, the representing vector is
{1,3,5} or {1,5,3} (leader is always in the front, other element is random depending on the union, the function of this is for the "2" function, where how i handle it is i first find the "leader" of the group (lets call it indeks i), then the element must be in v[i], so i erase the element from the vector, make the next first element in the vector the leader and adjust the rest of the vector, if the leader of the new vector (lets call it indeks j) is not i, swap it the vector i with vector j clear vector i;
my code: https://ideone.com/vZVvCn
however, im getting WA :( and i tried to debug it but no luck, can someone point out a counter case?
also, if there is a more optimal approach then my approach, please give me hints











bumping...
Disclaimer: Nobody's helped for three days so I'll try my best, but I'm tipsy so excuse me if the explanation is bad.
So, your code actually doesn't produce WA — it straight up crashes (on my PC at least). What actually confuses me is that you ask for a counter case — when the sample input is your counter case. You can check in the IDEONE you yourself linked that your output is not the sample output ("1 3" on last query instead of the correct "2 8"). This is due to undefined behaviour, and I can only guess that on your PC it actually produced the correct output.
Now your mistake is quite simple — your vector of vectors v is indexed from 0, while the elements are indexed from 1. You fill v in your first loop:
Since it's initially an empty vector obviously the indexing starts from 0. So in our sample test v[5] would actually be undefined and any access to it yields undefined behaviour.
The bad news are — the solution is slow. If you have some large vector and you apply operation 2 on it a lot of times, your complexity seems to be quadratic. I'll give my solution in a spoiler if you want to take a look. There's probably a much better one but this is the best I could come up with at 4 in the morning:
Note: You can solve the problem quickly and cleanly if you implement some set-like structure by using binary search trees yourself (for example, Treaps should work nicely). I was, however, too lazy to code BST, so my solution uses only arrays, but has 'leftover' elements at times, which may be confusing.
We'll keep groups of elements, similarly to your vectors. Initially every element is in it's own group. At any point we will know for each element in what group it is. Let's denote the group element K is in by groupid[K]. We'll also have some vectors that represent the groups, however those vectors might have leftovers of elements that are no longer in this group due to operation 2. This, however, won't be a problem. And of course, for each group we keep the sum and size of it.
For queries of type 1 we find for each element its group. We want to merge the two groups, so we pick the one whose group vector is smaller and iterate that. For each element in that group we check whether it really is in that group and not a leftover — if it really is from that group, then we move it to the other one, both by changing its groupid and by moving it in the other vector. After we're done iterating, we simply change the sum and size of the newly formed group by adding the values of the two initial groups.
For queries of type 2 we find in what groups the elements are. Let's say the query is a,b. We reduce the size of groupid[a] by 1 and it's sum by a, and do the same increase for groupid[b]. We then simply add a to the vector of groupid[b]. Notice that now a is in the vectors of two groups, but by updating groupid[a] we know where it truly is.
For queries 3 — simply print the values for the group of that element.
Here's my AC code with some comments.
ok, so i attempted the problem using set and taking your idea using arr groupid[]: https://ideone.com/c8agkn
but i am getting RTE, and debugging it myself fails :( a little help?
Extremely simple mistake — on line 15 the size of array s should be m+1 instead of n+1. That causes you to sometimes go out of bounds and RTE. Other than that it should work.
Using sets is indeed easier to implement and understand, but adds an additional log factor to the complexity. Amortized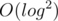 per query should still work quick enough, though (7s time limit is huge).
per query should still work quick enough, though (7s time limit is huge).
ouch, those mistakes are hard to find :(