How can Solve this problem. Need more explanation. Thanks in advance.
Please subscribe to the official Codeforces channel in Telegram via the link https://t.me/codeforces_official.
×
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/21/2024 17:30:41 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Lets define a function F(int nw, int nb, bool turn) which returns the probability of the princess winning from the state with nw white mouses and nb black mouses currently in the bag and if turn is false it is the princess turn to move and if turn is true it is the Dragon's turn to move.
From this we can see the answer to the original question is F(w, b, false)
First lets take the case where it is the princess's turn to move. For her to win, either she can directly pick a white mouse with probability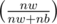 or she picks a black mouse with probability
or she picks a black mouse with probability 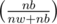 and for her to win we need to multiply this with F(nw, nb - 1, true). So, the princess's equation is :
and for her to win we need to multiply this with F(nw, nb - 1, true). So, the princess's equation is : 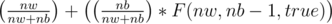
Now, lets take the case where it is the Dragon's turn to move. For the princess to win, the Dragon should always pick the black mouse which has probability (nb/(nw+nb)). Now, there can be two cases: the first one is that a white mouse escapes the bag and the second is that a black mouse escapes the bag.
Case 1 : White mouse escapes This happens with probability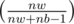 (-1 because the dragon already picked a black mouse). Now we have to multiply this with F(nw - 1, nb - 1, false) (Since, the dragon picked 1 black mouse and 1 white mouse escaped and 'false' since it will be the princess's turn to move now).
(-1 because the dragon already picked a black mouse). Now we have to multiply this with F(nw - 1, nb - 1, false) (Since, the dragon picked 1 black mouse and 1 white mouse escaped and 'false' since it will be the princess's turn to move now).
Case 2: Black mouse escapes This happens with probability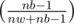 (Since Dragon already picked a black mouse, there will (nb-1) black mouses left). This should be multipled with F(nw, nb - 2, false) (Since, white mouse remains same and Dragon picked a black mouse and another black mouse escapes).
(Since Dragon already picked a black mouse, there will (nb-1) black mouses left). This should be multipled with F(nw, nb - 2, false) (Since, white mouse remains same and Dragon picked a black mouse and another black mouse escapes).
So, the equation for dragon's move will be: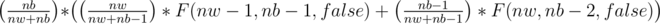
We can declare an array dp[white][black][turn] to store the results so that it is not computed again. So, the overall complexity would be O(2wb)
We should also handle cases where, nw is 0 or nb is 0 or negative and return appropriate values.
Accepted Solution in C++