Here are the editorials for all the problems. Hope you enjoyed them and found them interesting!
Tutorial is loading...
Code
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int INF = 1e9 + 7;
const int MOD = 1e9 + 7;
const int N = 1000;
char bus[N][5];
void printbus(int n)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < 5; j++)
{
cout << bus[i][j];
}
cout << '\n';
}
}
void yes()
{
cout << "YES" << '\n';
}
void no()
{
cout << "NO" << '\n';
}
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int n; cin >> n;
for(int i = 0; i < n; i++)
{
for(int j = 0; j < 5; j++)
{
cin >> bus[i][j];
}
}
bool possible = false;
for(int i = 0; i < n; i++)
{
for(int j = 0; j < 2; j++)
{
if(bus[i][j*3] == 'O' && bus[i][j*3+1] == 'O')
{
bus[i][j*3] = '+';
bus[i][j*3+1] = '+';
possible = true;
break;
}
}
if(possible) break;
}
if(!possible)
{
no();
return 0;
}
else
{
yes();
printbus(n);
return 0;
}
return 0;
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int INF = 1e9 + 7;
const int MOD = 1e9 + 7;
const int LG = 20;
ll a[1001][1001];
ll r[1001]; //row sum
ll c[1001]; //column sum
int n;
void no()
{
cout << -1 << '\n';
}
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
cin >> n;
int x, y; ll diagonal1 = 0; ll diagonal2 = 0;
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
cin >> a[i][j];
if(a[i][j] == 0)
{
x = i; y = j;
}
else
{
r[i] += a[i][j];
c[j] += a[i][j];
if(i == j)
{
diagonal1 += a[i][j];
}
if(i + j == n - 1)
{
diagonal2 += a[i][j];
}
}
}
}
if(n == 1)
{
cout << 1 << '\n';
return 0;
}
ll commonsum = r[0];
if(x == 0) commonsum = r[1];
//cout << commonsum << '\n';
ll rowsum = -1; ll colsum = -1; ll d1sum = -1; ll d2sum = -1;
for(int i = 0; i < n; i++)
{
if(i != x)
{
if(r[i] != commonsum)
{
no();
return 0;
}
}
else
{
rowsum = r[i];
}
}
for(int i = 0; i < n; i++)
{
if(i != y)
{
if(c[i] != commonsum)
{
no(); return 0;
}
}
else
{
colsum = c[i];
}
}
bool isdiagonal1 = false; bool isdiagonal2 = false;
if(x == y) isdiagonal1 = true;
if(x + y == n - 1) isdiagonal2 = true;
if(!isdiagonal1)
{
if(diagonal1 != commonsum)
{
no();
return 0;
}
}
else
{
d1sum = diagonal1;
}
if(!isdiagonal2)
{
if(diagonal2 != commonsum)
{
no();
return 0;
}
}
else
{
d2sum = diagonal2;
}
if(rowsum == colsum)
{
if(isdiagonal1 && d1sum != rowsum)
{
no();
return 0;
}
if(isdiagonal2 && d2sum != rowsum)
{
no();
return 0;
}
ll value = commonsum - rowsum;
if(value > 0)
{
cout << value << '\n';
return 0;
}
else
{
no();
return 0;
}
}
else
{
no();
return 0;
}
}
Tutorial is loading...
Code (O(nkm^2))
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int N = 101;
const int MOD = 1e9 + 7;
const ll INF = ll(1e18);
ll dp[N][N][N];
int c[N];
ll cost[N][N];
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int n, m, k; cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
{
cin >> c[i];
}
for(int i = 0; i <= n; i++)
{
for(int j = 0; j <= k; j++)
{
for(int a = 0; a <= m; a++)
{
dp[i][j][a] = INF;
}
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> cost[i][j];
}
}
if(c[1] == 0)
{
for(int i = 1; i <= m; i++)
{
dp[1][1][i] = cost[1][i];
}
}
else
{
dp[1][1][c[1]] = 0;
}
for(int i = 2; i <= n; i++)
{
for(int j = 1; j <= k; j++)
{
if(c[i] == 0)
{
for(int a = 1; a <= m; a++)
{
dp[i][j][a] = min(dp[i][j][a], dp[i-1][j][a] + cost[i][a]);
for(int b = 1; b <= m; b++)
{
if(b != a) dp[i][j][a] = min(dp[i][j][a], dp[i-1][j-1][b] + cost[i][a]);
}
}
}
else
{
dp[i][j][c[i]] = min(dp[i][j][c[i]], dp[i-1][j][c[i]]);
for(int b = 1; b <= m; b++)
{
if(b != c[i]) dp[i][j][c[i]] = min(dp[i][j][c[i]], dp[i-1][j-1][b]);
}
//cout << i << ' ' << j << ' ' << c[i] << ' ' << dp[i][j][c[i]] << '\n';
}
}
}
ll ans = INF;
for(int i = 1; i <= m; i++)
{
ans = min(ans, dp[n][k][i]);
}
if(ans >= INF) ans = -1;
cout << ans;
}
Code (O(nkm))
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int N = 101;
const int MOD = 1e9 + 7;
const ll INF = ll(1e18);
ll dp[N][N][N];
int c[N];
ll cost[N][N];
ll idx[N][N];
ll m1[N][N];
ll m2[N][N];
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0);
int n, m, k; cin >> n >> m >> k;
for(int i = 1; i <= n; i++)
{
cin >> c[i];
}
for(int i = 0; i <= n; i++)
{
for(int j = 0; j <= k; j++)
{
m1[i][j] = INF; m2[i][j] = INF; idx[i][j] = -1;
for(int a = 0; a <= m; a++)
{
dp[i][j][a] = INF;
}
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> cost[i][j];
}
}
if(c[1] == 0)
{
for(int i = 1; i <= m; i++)
{
dp[1][1][i] = cost[1][i];
if(dp[1][1][i] <= m1[1][1])
{
if(dp[1][1][i] == m1[1][1])
{
idx[1][1] = -2;
}
else
{
idx[1][1] = i;
}
m2[1][1] = m1[1][1];
m1[1][1] = dp[1][1][i];
}
else if(dp[1][1][i] <= m2[1][1])
{
m2[1][1] = dp[1][1][i];
}
}
}
else
{
dp[1][1][c[1]] = 0;
m1[1][1] = 0; idx[1][1] = c[1];
}
for(int i = 2; i <= n; i++)
{
for(int j = 1; j <= k; j++)
{
if(c[i] == 0)
{
for(int a = 1; a <= m; a++)
{
dp[i][j][a] = min(dp[i][j][a], dp[i-1][j][a] + cost[i][a]);
ll tmp = INF;
if(a == idx[i-1][j-1])
{
tmp = m2[i-1][j-1];
}
else
{
tmp = m1[i-1][j-1];
}
dp[i][j][a] = min(dp[i][j][a], tmp + cost[i][a]);
}
}
else
{
dp[i][j][c[i]] = min(dp[i][j][c[i]], dp[i-1][j][c[i]]);
for(int b = 1; b <= m; b++)
{
if(b != c[i]) dp[i][j][c[i]] = min(dp[i][j][c[i]], dp[i-1][j-1][b]);
}
//cout << i << ' ' << j << ' ' << c[i] << ' ' << dp[i][j][c[i]] << '\n';
}
for(int a = 1; a <= m; a++)
{
if(dp[i][j][a] <= m1[i][j])
{
if(dp[i][j][a] == m1[i][j])
{
idx[i][j] = -2;
}
else
{
idx[i][j] = a;
}
m2[i][j] = m1[i][j];
m1[i][j] = dp[i][j][a];
}
else if(dp[i][j][a] <= m2[i][j])
{
m2[i][j] = dp[i][j][a];
}
}
}
}
ll ans = INF;
for(int i = 1; i <= m; i++)
{
ans = min(ans, dp[n][k][i]);
}
if(ans >= INF) ans = -1;
cout << ans;
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define fbo find_by_order
#define ook order_of_key
typedef long long ll;
typedef pair<int,int> ii;
typedef vector<int> vi;
typedef long double ld;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
typedef set<int>::iterator sit;
typedef map<int,int>::iterator mit;
typedef vector<int>::iterator vit;
const int INF = 1e9 + 7;
const int MOD = 1e9 + 7;
const int N = 1e6 + 3;
int a[N];
int visited[N];
ll ans;
vector<int> cycles;
ll dp[N];
int cyclecnt;
void dfs2(int u)
{
cycles[cyclecnt]++;
visited[u] = 3;
if(visited[a[u]] == 3) return ;
dfs2(a[u]);
}
void dfs(int u)
{
visited[u] = 2;
if(visited[a[u]] == 0)
{
dfs(a[u]);
}
else if(visited[a[u]] == 1)
{
visited[u] = 1;
return ;
}
else
{
cycles.pb(0);
dfs2(u);
cyclecnt++;
}
visited[u] = 1;
}
int main()
{
//ios_base::sync_with_stdio(0); cin.tie(0);
int n; scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
scanf("%d", a + i);
}
dp[0] = 1;
for(int i = 1; i <= n; i++)
{
dp[i] = (dp[i-1]*2LL)%MOD;
}
ans = 1;
memset(visited, 0, sizeof(visited));
for(int i = 1; i <= n; i++)
{
if(visited[i] == 0)
{
dfs(i);
}
}
ll cnt = n;
for(int i = 0; i < cycles.size(); i++)
{
cnt -= cycles[i];
ans = (ans*(dp[cycles[i]]-2+MOD))%MOD;
}
ans = (ans*dp[cnt])%MOD;
if(ans < 0) ans += MOD;
int ans2 = ans;
printf("%d\n", ans2);
return 0;
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef vector<int> vi;
const int MOD = 1e6 + 3;
ll power(ll base, ll exp)
{
ll ans = 1;
while(exp)
{
if(exp&1) ans = (ans*base)%MOD;
base = (base*base)%MOD;
exp>>=1;
}
return ans;
}
int main()
{
ios_base::sync_with_stdio(false); cin.tie(0);
ll n, k;
cin >> n >> k;
if(n <= 63 && k > (1LL<<n))
{
cout << 1 << " " << 1;
return 0;
}
ll v2 = 0;
int digits = __builtin_popcountll(k - 1);
v2 = k - 1 - digits;
ll ntmp = n % (MOD - 1);
if(ntmp < 0) ntmp += (MOD - 1);
ll ktmp = k % (MOD - 1);
if(ktmp < 0) ktmp += (MOD - 1);
ll v2tmp = v2 % (MOD - 1);
if(v2tmp < 0) v2tmp += (MOD - 1);
ll exponent = ntmp*(ktmp - 1) - v2tmp;
exponent %= (MOD - 1);
if(exponent < 0) exponent += MOD - 1;
ll denom = power(2, exponent);
ll numpart = 0;
if(k - 1 >= MOD)
{
numpart = 0;
}
else
{
ll prod = 1;
ll ntmp2 = power(2, ntmp);
prod = power(2, v2tmp);
prod = power(prod, MOD - 2);
if(prod < 0) prod += MOD;
for(ll y = 1; y <= k - 1; y++)
{
prod = (prod * (ntmp2 - y))%MOD;
}
numpart = prod;
}
ll num = (denom - numpart)%MOD;
num %= MOD; denom %= MOD;
if(num < 0) num += MOD;
if(denom < 0) denom += MOD;
cout << num << " " << denom;
return 0;
}










Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Nice editorial!
It will appear after system tests.
Hey , http://codeforces.com/contest/711/submission/20254708 why does this time out ?
Why use a "For" loop for calculating power of 2? Use Modular exponentiation by Squaring instead.
Although a log(N) time complexity for computing the product is not the cause for the time out, I strongly recommend you to learn the fast exponential function.
I am still reading the code to see if there is a possible infinite loop.
Edit:
Try this case:
5
2 3 1 3 4
You failed to handle cycles properly.
Edit: I think my English got murdered today.
Thanks , btw what is the output of that operation ?
24 if I am not mistaken, my code just passed the system test so it should be correct.
Problems were very nice: short and to the point! Editorial was also given so fast, and the queue also displayed the verdict on time without any delays. Everything was perfect and I solved 4 problems until I received "WA on 105" in C.
I got "WA on 92" in B, great feeling.
I'm on 94
My friend on 95
Now i got "WA on 100" ;)
Oh boy, I get that pain when you fail to implement an easy solution. Feels bad to also fail in C.
The main blog was deleted?
Sorry it was my fault. I accidentally clicked "Save Draft" when I was trying to publish the winners and it went missing. It is back now.
For what test cases would these 2 solution for A and B not work? :(
2A — http://ideone.com/He9UCX
2B — http://ideone.com/ymynPJ
For 2A, it's incorrect if there is "XX|OO" where this is the first available row.
For 2B you didn't take care of n=1
I failed on C because I declared the array as n*k*n instead of n*k*m..and problem b because I didnt verify the boolean in case the answer is not possible,,,Yes, these are the mistakes I made.. Today d saved me, otherwise my day could have been 100x worse...Nice problems. I was 120 before sys tests, 830 afterwards..Thats life mate...
Same story about problem C. Solution was correct, but final cycle to find minimum value from last colors was from 1 to n instead of m.
Could someone please explain Problem D more clearly. Do we just find the connected components using kosaraju's method and then proceed?
First, consider the original oriented graph. Each node has exactly one edge going out. If we start at some point, we can follow the edges and obviously we will get looped (e.g. 1-2-3-4-5-3). For points inside loop, we will always stay inside loop. For other points, they will fall into some loop eventually.
Conclusion: the graph consists of several disjoint cycles, and there are some "free" paths leading from "leaves" into some cycle. These paths do not intersect (only in cycle points).
Now consider the unoriented graph, i.e. remove all directions. We can orient those "free" paths arbitrarily, independently: 2num_free_edges. And for each cycle, there are only two edge orientations that are bad for us — full clockwise cycle and full ccw cycle. Therefore for each cycle of length c we need to multiply the answer by 2c - 2.
How to find cycles? We always have only one edge outgoing from any node (in the original directed graph). Let's go from each node and follow the edges until we meet an already visited node. We also keep track whether the node's cycle was already counted, and a "time" counter. Then when we get to the node second time, we check if its cycle was already counted and if not, we use the time difference to get the cycle length.
Yes, finding strongly connected components with Tarjan or Kosaraju and the rest you can solve by fast exponentiation.
Thank you. :)
We don't need to find strongly connected components in this problem, since if we make the graph undirected, there will be only one simple cycle in each component, and we can find it by simply dfs and find the only back edge.
Problem E. Why do we calculate complement probability as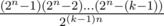 but not as
but not as 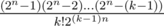 (with k! in denominator) ?
(with k! in denominator) ?
'cause we define the probability that no two ones have the same birth day as follow : k! *c[2^n][k] /((2^n)^k) now if u decompose c[2^n][k] in the numerator , u can find that we can delete the k! from both the numerator and denominator .
this is true when k<=2^n
how from the problem statement follows that order matters? when I read it I thought, that order does not matter and therefore the probability you are speaking about is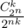 , not
, not 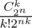 .
.
I'm late but I'll try to explain. I think it's because the order in which we choose the birthdays matters, i.e. we assumed the i-th paranthesis in the numerator refers to the birthday of the i-th person.
Example: let's have 3 days in a year (A, B, C) and 2 people.
If we use the second formula you wrote, we'd have 3 cases for 'distinct birthdays': one person is born on A and the other on B, one is born on A and the other on C; and one is born on B and the other on C.
If we use the author's formula we would have 6 cases for 'distinct birthdays'.
For 2E, why for test case 4 the output has to be "906300 906300"? Wouldn't "1 1" be the same?
Because you want original numbers to be coprime (not the answer after modulus)
==> If it would be possible, the process would be following: A) Find two numbers B) Make them coprime C) Do modulo operation
Here, it can happen that two numbers can be coprime, but after modulo, the results are not:
Little example: A=3,B=8,MOD=5
A and B are coprime, but "A % MOD" and "B % MOD" (3 / 3) are not!
Good Luck & Have Nice Day! :) ^_^
But since k > MOD, A is guaranteed to be equal as B. What I don't get is why I must output (B%MOD)/(B%MOD) while 1/1 is not accepted . @_@
UPD: Ahh I think I got it.
My codes were accepted during the system checking but now its showing skipped and there is no change in my rating.My all submissions of the contest are showing "skipped". Can somebody please help me regarding this issue?
Probably your codes were very similar to some one else.
I have a tendency of writing recursive solutions for DP problems. Will that be cause any problem in near future? Here is my accepted solution for DIV 2C (Complexity O(NKM2)). Can anyone help how to modify the same recursive solution so that complexity is reduced to O(NKM).
Can't find why is this WA?
dunnow why this results WA
http://codeforces.com/contest/711/submission/20256542
solved it ... thanks
Silly doubt, but really helpful. What happens if k>n in Problem C. How does DP gives answer for that case?
supposing that ur dp parameters are :
1 : the index of the tree (ind)
2: how many different groups u have till now (diff)
3: and the previous color (prev)
of course when u reach ind=n(if u start enumerating the trees from 0 ,then u processed all the trees) and diff< k return oo ,
so at the end ,when u finish ur dp function , if the result >= oo ,then there is no way to get k different groups ,so print -1;
But, how to prove that when k>n, result will be INF according to the dp made in editorial?
You just don't have enough trees to have k groups.
In the editorial for E, these 2 lines are used to calculate the highest power of 2 which divides 1.2.3...k-1.
int digits = __builtin_popcountll(k — 1);
v2 = k — 1 — digits;.
Can somebody please elaborate on this formula.
Never mind!
For problem E, I think it should be (k-1)<MOD and not (k-1)<=MOD.
For problem c, Why complexity nkm^2 can pass all the test as n=k=m=100?
Won't it be TLE?
During the contest, I considered the solution of nkm^2. But because I am afraid to be TLE, I didn't write it.
sad...:(
Now you know, 108 simple operations can be completed in < 1 second on Codeforces.
Oh maybe I am wrong, I always consider n2 for N = 103, n3 for N = 102,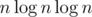 or
or 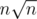 for N = 105
for N = 105 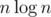 for N = 2 × 105.
for N = 2 × 105.
Maybe my entire outlook should be changed...
for problem E : can anyone explain the details of the last part of the author's code — calculating and reducing the numerator — thanks in advance
Can you give me a webite link to explain "Legendre's formula" in the editorial of Problem E? I know nothing about that:(
Here you go : Link
Can someone explain the Div 2C in a top- down manner? I am not able to understand the editorial.
Thanks!
the function would look like this
now :the index of the current tree, k :the number of contiguous groups until now, prev : the color of the previous tree.
now for every uncolored tree you should try each color then move to the next tree then minimize the result, if the the tree is colored just ignore it. but remember to increase k when you find two adjacent trees with different colors , when you reach the end just see if k equals the given number of beauty otherwise it is not a valid solution. here is my solution
I did not get this line in first problem
please explain.
The cycle for j is from 0 to 1. So on the first iteration we have 3 * j and 3 * j + 1 equals to 0 and 1. That's indexes of the first pair seats. On the second we have 3 * j and 3 * j + 1 equals to 3 and 4. That's indexes of the second pair seats.
I didnt understand how
problem-Cwas done inO(nkm). Can anyone please help. In the code given in editorial what is the purpose of m1[][], m2[][] and idx[][].m1- global minimum for i-th for pretty k, m2- the second minimum, idx-where we can find it!
Thanks, one more doubt, what does idx[][] = -2 mean? Does it mean that 2 minimum paths are possible so we can always pick minimum?
Yes
My submission on B got wrong answer on test case 32. But I still don't understand what was wrong with my logic. I calculate D=max(all rowsum,all columnsum,diagonal1,diagonal2)-min(all rowsum,all columnsum,diagonal1,diagonal2) . Then I added D(if D>0) to empty cell and updated all sums. Then I recheck if(max(all rowsum,all columnsum,diagonal1,diagonal2)-min(all rowsum,all columnsum,diagonal1,diagonal2) == 0) then print D, else -1. I have also taken care of n==1 case. Here's my Submission. Can someone point out my mistake?
Ohh! What a silly mistake! Thanks a lot for pointing it out.
Hey guys, I'm stuck at Problem D test 7 for 2 hours. I'don't know where did I get wrong.
can somebody help please? I can't appreciate you more. Here's my code: 20279080
Did you get your mistake ?
sadly no :(
if i'm not too late.
consider this case
5
2 3 4 3 1
you output 8 but the answer is 16
how can i draw the 3 dimentional dp array in a piece of paper for problem C
You don't need to think in 3 dimensions for this problem. When you're considering the i'th tree, all you need to know is the states from the previous tree i - 1.
All you need to keep in your head is 2 planes. Each plane contains all the possible states for the corresponding tree. We only need to know how these planes relate to each other, namely, how can we compute i'th plane from i - 1 plane.
I imagine planes made from pixels (like monitor). These planes are almost transparent, so that I can put one screen on top of the other and see the screen on the bottom through the screen on top. I know the values of the pixels of the bottom screen and I need to calculate the values of the pixels of the top screen.
To traverse all the pixels of the screen on top we need 2 loops:
To compute the value of the single pixel of the
top_screen[x][y]we need to consider all of the points of thebottom_screen[][]. So, each pixel in the bottom screen contributes it's value to the pixeltop_screen[x][y]. To traverse all of the pixels of the bottom screen we also need 2 nested loops:When we combine these thoughts together, we get a general structure for the program:
I have a question regarding the C problem: could you please explain what does the "last colour" and "current colour" mean?
Problem E is very interesting.
Is there an intuitive way to deduce the Legendre's Formula? I couldn't figure it out, I had to read a Wikipedia article :/
I thought like this: we have numbers 1,2,3,...,k-1 and we want to divide by 2 as many of them as possible and as many times as possible. First we count all even numbers, we divide them by 2: there are floor((k - 1) / 2) even numbers there. Then we count numbers divisible by 4. We have already divided them by 2, so we have to count them only once: floor((k - 1) / 4). Continuing, we get that the total product is 2t, with
Hello. In problem E 'One way to resolve this is to reduce it modulo MOD - 1, since 2MOD - 1 ≡ 1 modulo MOD by Fermat's Little Theorem.' I could not understand this. Why we take MOD — 1? If anyone could explain in details I would be gratified. Many thanks in advance.
Fermat's Little Theorem states that ap ≡ a (mod p) // (if p is prime)
In other words ap - 1 ≡ 1 (mod p) // (if a is not divisible by p)
So instead of calculating xy (mod p) we can calculate x(y mod(p - 1)) (mod p). We can do that because of the second equation. We just substract p-1 from the exponent as long as we can since multiplication by 1 doesn't change the result.
In the solution of problem 711C, why the elements of dp array are being initialised to INF, when every time they are being updated by dp[i][j][a-1]+c[i][a-1]. Please clear my doubt
dp[][][] array is initialized to INF as we need to find minimum value, that is why you can see a min() function called each time when updating dp[][][] value
can the problem C be done using 2-D dp arraay ? if yes, how ?
I think No, as the state requires 3 information to goto a unique next state. Anything less than 3 information per state will give us more than 1 state to goto, so we wont be able to decide which one to go for.
Can somebody help take a look and point out what's wrong with my code for problem E? Thanks in advance. =D
http://codeforces.com/contest/711/submission/20341261
What do you do
?
Change it to
.
If the real answer is you output p mod MOD and q mod MOD.
you output p mod MOD and q mod MOD.
Oh boy, that was dumb of considering p mod q instead of (p-q) mod MOD. :P
Thanks for the help!
could somebody help me with question 711C
i am getting WA on test on test 12. I have applied the logic correctly, I guess so,
here is the code http://ideone.com/OW6sYs
Thnks
I am afraid that INT_MAX is not good enough to be used as INF in this question.
thank you very much!!
I changed it into 10^15+5 and it worked. ACCEPTED.
But even LONG_MAX doesn't work and why does LONG_MAX gives negative values. Please suggest.
LONG_MAX = 2^32-1 is approximately 2e9, so it is still not good enough to be considered as INF.
I am not sure about what did you type in your code to make LONG_MAX becomes negative, but chances are you are not doing something like (LONG_MAX + FOO) so it overflows and becomes negative.
In problem D, what if a road is part of two cycles. Say city 1->2->3->4->1 and 2->3->5->2 does the description above satisfy that case? Say, for 1,2,3,4 when we are considering the fact that 2->3 is flipped and becomes 3->2 we must not count the same case for the 2,3,5 component. Because they are the same. I am asking this question because there is no mention, that a road cannot be part of two different cycles.
As we have just one directed edge out from each node, each connected component(not scc) of the graph will have exactly one cycle. Thus an edge must belong to at max one cycle.
In problem E : doubts regarding MOD: 1. in denom plz explaing the MOD-1 logic 2. in calculating numerator it should be multiplied by pow(2, -vtmp) right ?? But why it is multiplied by pow(pow(2, vtmp), MOD — 2 ) ?? 3. How does builtin_pop_count help here ?? vtmp stands for power of 2 in gcd right ?
I assume that you know neither Fermat's Little Theorem nor Euler's extension on it. I strongly recommend you to Google it, it's is fundamental for handling modulus equations.
This is because a^(p-1) = 1 mod p (where p is a prime), that means that we can reduce a^x to a^(x%(p-1)) since a^n has a cycle of p-1.
This is the inverse function, this is a pretty common thing so I would leave it for Google to explain the meaning of a^-1 MOD b.
I got the theorem Just cant figure out the reduction done in the power :(
nvm Got it :)) Pen and paper work helped clear it out :))
zscoder can you tell me my mistake in test case 7 on Div2 D http://codeforces.com/contest/711/submission/20560676
Could anyone explain me the following:
ll cnt = n; for(int i = 0; i < cycles.size(); i++) { cnt -= cycles[i]; // Why? ans = (ans*(dp[cycles[i]]-2+MOD))%MOD; // Why adding MOD and then %MOD? } ans = (ans*dp[cnt])%MOD; // What is the goal?Adding MOD then %MOD is to make sure the answer is always positive.
I'm doing what I explained in the editorial, for each cycle with length cycles[i] I multiply the answer by 2cycles[i] - 2 and for each remaining edge that aren't in any of the cycles I'm multiplying the answer by 2.
Hi everyone,
could anyone explain how the answer of this test of problem D would be as explained in the editorial
7
1 2
2 3
3 1
2 4
4 3
3 5
5 1
I wonder if some changes can be made to make my recursive solution of div2C accepted. Also, can anyone help me in finding its time complexity ? ( watch our for exit conditions )
Yeah...! This is possible, You just have to store the state values. And whenever you encounter an already solved state, you can get the value in O(1) time. (DYNAMIC PROGRAMMING)
Your recursive solution with memoization
Can somebody explain the O(nkm) approach of div2C?
Can somebody explain the O(nkm) approach of div2C?
In D, how can there be a path, shouldn't every component contain a cycle? Please help.
Okay, sorry for the stupid way of asking what I wanted to ask But this is what I wanted to know. 1 . Why are we not converting the graph to undirected graph, because if there is a undirected cycle in any component, we can always fina directed cycle by changing the orientation of the edges. 2. How can there be a path? A path would mean there is so undirected cycle, hence a component can have only x-1 edges,where x is the number of vertices in the component. But each component should have equal number of vertices and edges, as when you sum up number of vertices and edges, in the end you should get n vertices and n edges.
Someone please help me. zscoder 1.
Yea you are right.
zscoder For Div 2B There is testcase
by observation output should be 1 but they are expecting -1 , Can you plz tell me why is it so ??
The main diagonals must also have the same sum as the rows and columns.
zscoder is so nice, always replying to his contest editorials
respect++
242974284 For Problem D: Directed Roads Can someone please tell why I am getting TLE on TC 7, I think it is O(n) solution basic dfs similar to editorial.