It is known (well, as long as Tarjan's proof is correct, and it is believed to be) that DSU with path compression and rank heuristics works in O(α(n)), where α(n) is an inverse Ackermann function. However, there is a rumor in the community that if you do not use the rank heuristic than the DSU runs as fast, if not faster. For years it was a controversial topic. I remember some holywars on CF with ones arguing for a random heuristic and others claiming they have a counter-test where DSU runs in 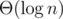 independently of rand() calls.
independently of rand() calls.
Recently I was looking through the proceedings of SODA (a conference on Computer Science) and found a paper by Tarjan et al. The abstract states:
Recent experiments suggest that in practice, a naïve linking method works just as well if not better than linking by rank, in spite of being theoretically inferior. How can this be? We prove that randomized linking is asymptotically as efficient as linking by rank. This result provides theory that matches the experiments, which implicitly do randomized linking as a result of the way the input instances are generated.
This paper is relatively old (2014), though I haven't yet heard of it and decided to share with you.
A whole paper can be found here.











In practice it is about twice slower, isn't it?
On average testcase work (time of usual implementation with rand) = (time of rand) + (time of usual implementation without rand).
On the worst testcase: (time of usual implementation with rand) = (time of rand) + (time of usual implementation without rand) / 2.
In practice path-compression without rank-heuristic works in constant time.
What about that version? What is its complexity?
Amortized O(log n) per operation.
How to prove that?
EDIT: Providing both proof and worst case test would be nice.
Well, I know the proof that it's :
:
http://cs.stackexchange.com/questions/50294/why-is-the-path-compression-no-rank-for-disjoint-sets-o-log-n-amortized-fo/50318#50318
EDIT: This paper by Tarjan and van Leeuwen gives pictures with worst-case examples, (see pages 262-264), and a slightly different proof of the fact that it is O(log n): http://bioinfo.ict.ac.cn/~dbu/AlgorithmCourses/Lectures/Union-Find-Tarjan.pdf
I think, you skiped a return before
rep[v] = Find(rep[v])Thanks, it seems even the simplest possible F&U version cannot be written without a bug ; p. At least that's the kind of bug compiler would tell me about :).
Can anyone show me an example of m (union/find) operations that traverses more than 2* min (n, m) edges?
When I do a "find" or "union" operation, it requires a constant time * (number of edges in the path to the root). If I divide these edges in two groups: immediate edge (the first edge in the path) and intermediate edges (the remaining edges). I can easily see that each edge will be an intermediate edge at most once, because we have the path compression. So, the number of intermediate edges will be at most n (number of union/find calls). And obviously, the number of immediate edges will be at most to n.
The conclusion is that the total time required for the union/find operations will be constant * (2 * n). Therefore, each operation union/find operation costs O(1) amortized.
**P.S: ** Someone corrects me, if I'm wrong.
I saw my mistake, the statement that "each edge will be an intermediate edge at most once" is false.
You may also find this blog post on Codeforces interesting where natsukagami was wondering why a simple link heuristic was faster than link-by-size. In the comments I mentioned that he was using link-by-index.
Maybe the sence is: in random case it works in average with same asymptotic, but with rank heuristic in worth case ?
Yes, you're right. In case of randomized algorithms the average case is analysed almost always. But this is not the point -- the rumor was that random linking may work on θ(logn) on average, which was disproved by Tarjan.
After short discussion ifsmirnov agreed that the post misleads readers.
Let's read the given paper attentively.
We analyze randomized linking and randomized early linking, which are linking by index and early linking by index with the elements ordered uniformly at random.
Authors prove that
joinIndexworks in O(α(n)).Usual
join, which uses random in following way:reduces depth only in two times. So with path-compression it works in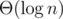 in the worst cast. And without path-compression it works in Θ(n) in the worst case.
in the worst cast. And without path-compression it works in Θ(n) in the worst case.
I still haven't heard of any counter-random test. I even actually believed in power of join with random and stopped writing with rank.
One such test would be:
Let's prove that random linking runs in expected O(N) time without path compression and O(log N) with it. First, realize that, in reality, find's run time is directly proportional to the length of the longest path, which will always be part of 1's connected component in such a case. Knowing the longest path always increases by at most 1 every union, we only care about the expected number of longest path increases, or, by linearity of expectation, the probability of an increase happening on one particular iteration. This probability is exactly , thus the expected number of increases is
, thus the expected number of increases is 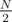 .
.
If we want to include path compression, the complexity drops down to O(log N) even without random linking. The hardest part would be proving it to be Ω (log N). Though harder in theory, the fact that random linking provides linear expected heights while rank heuristics provide logarithmic expected heights makes for enough intuitive evidence of this fact (this goes by the same lines as Burunduk1).
Do you mean that DSU with path compression and random linking will work O(NlogN) in total on this test?
Probably not on this test alone. The main point of the test is to show random linking won't decrease height asymptotically, so random linking is no better than father[a] = b type linking, which in itself runs in O(log N).
You haven't proved anything. Burunduk1 already showed me this test couple of years ago, but I think it's still n alpha(n). I want test with nlogn.
I think that here is something similar to O(nlogn):
http://ideone.com/iUu2S3
http://ideone.com/j7QnvP
It does. I changed your code a little bit to compare my ways of implementation and the new "indexes" one.
Here's the result:
RANDOM:
res[1.0e+04] = 5.872
res[1.0e+05] = 6.667
res[1.0e+06] = 7.450
res[1.0e+07] = 8.227
RANKS:
res[1.0e+04] = 2.691
res[1.0e+05] = 2.692
res[1.0e+06] = 2.691
res[1.0e+07] = 2.691
INDEXES:
res[1.0e+04] = 3.791
res[1.0e+05] = 3.838
res[1.0e+06] = 3.998
res[1.0e+07] = 3.825
That's the code: https://pastebin.com/mFCP6511
Now it's obvious: random is NOT as good as ranks or indexes. I hope the question is closed.
You've given right Ω(n) test for case "without path compression".
But, I agree with -XraY-, test against "path compression" is more complicated. Because even simpler question "how to make path compression be amortized ω(1)?" is not so easy.
The test for path compression:
If there is no random (join makes just
p[a] = b) "while" loop will do exactly one iteration. With random expected number of iterations is 2.The time of i-th get is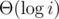 . To prove it we have to draw some pictures, after 2k calls of "get" our tree will be Tk, k-th binomial tree (Tk = Tk - 1 + Tk - 1, add the second root as child of the first one).
. To prove it we have to draw some pictures, after 2k calls of "get" our tree will be Tk, k-th binomial tree (Tk = Tk - 1 + Tk - 1, add the second root as child of the first one).
For future reference, I posted a potential proof of an $$$\Omega\left(n \frac{\log n}{\log \log n}\right)$$$ lower bound for path compression with linking by flipping a fair coin, if we allow the queries to be interactive (i.e. depend on the result of earlier find queries), in this thread.