Here are the authors of the problems:
- A — Written by GlebsHP, prepared by vovuh
- B — Written by GlebsHP, prepared by vovuh
- C — zxqfl
- D — Errichto
- E — zxqfl
- F — zxqfl
- G — KAN
I'd like to thank the Codeforces team for their help, particularly KAN, who was the tester for this round.
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...










Problem E:
find the next coin that Alfred will use (this can be done in O(1) with O(c) pre-processing)But how can this be done? I don't see the way... :(
Keep an array a such that a[i] gives the most valuable coin that is not worth more than i dollars.
Oh, that's smart. But I should fast modify this array every time I try new answer, shouldn't I? So should I use something like segment tree or is there simpler solution?
Just check whether this coin would be better than the coin you get from performing the array lookup. There's only 1 coin that needs to be added, so it's still O(1).
That's it, thank you!
No problem.
I can't understand proof for problem E.
Can someone help me with some different explanation?
Appreciate the help!
Me neither. Can someone kindly explain again ?
Problem E:
Imagine you have N coins. First you put a frequency array for each coin and also a lookup array where NEXT[c] = (greater coin that does not exceed c), both can be done in O(N) precomputation. The thing is this will help us simulate the algorithm in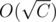 , starting with C (total cost) we can get NEXT[C] and subtract all the coins possible from C this is done with min(FREC[NEXT[C]], C / NEXT[C]). The thing is that all the coins subtracted in each step are different. Since they are different, it is not POSSIBLE to have subtracted more than
, starting with C (total cost) we can get NEXT[C] and subtract all the coins possible from C this is done with min(FREC[NEXT[C]], C / NEXT[C]). The thing is that all the coins subtracted in each step are different. Since they are different, it is not POSSIBLE to have subtracted more than 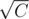 different number without exceeding C. This can be seen assuming the worst case of numbers subtracting
different number without exceeding C. This can be seen assuming the worst case of numbers subtracting 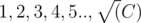 which will sum up to C or more. So our simulation is efficient. Now we need to run the simulation with each coin. The thing is, giving only one coin will give the same result than giving multiples (proof below). So we can run the simulation with each possible coin from 1 to C.
which will sum up to C or more. So our simulation is efficient. Now we need to run the simulation with each coin. The thing is, giving only one coin will give the same result than giving multiples (proof below). So we can run the simulation with each possible coin from 1 to C.
Proof for needing only one coin: If you remove coins in order -> S - c1 - c2 - x - c3 - c4 - c5 - y - c6... then it is proven that instead of subtracting x in step three we can subtract x+y and he will pick the same set of coins. We know for sure that S - c1 - c2 - x - c3 - c4 - c5 > = y + c6..., accommodating this expression we have S - c1 - c2 - x - y > = c3 - c4 - c5 - c6... and also choosing y before will not add another coin between y and c3, because the sum at that point is even greater. With this we proved that the set of coins will be the same giving him x+y or (x and y).
Editorial for problem D seems to be missing, where can i find it?
You can simply simulate the process. Limak will always try to disqualify the team which has higher number of balloons than him and which can be disqualified with the least cost (cost = weight_of_team — no_of_balloons + 1). Put all the teams with more balloons than Limak's team in a priority queue and keep disqualifying the best choice. When you disqualify a team, the count of Limak's balloons decreases so you may need to push more teams in the priority queue (this can easily be done by maintaining a global sorted list of teams based on non-increasing order of total initial balloons, and you simply need to pop from the back). Do this process until no more teams can be disqualified. The final ans is 1 + minimum size of priority queue during all these steps. I used binary search in my code but it is not needed.
And the complexity is O(n(logn)^2)
Am I the only one who don't understand the samples in problem F ?
can someone please explain it ?
Here are the optimal moves, I will leave the task why is this optimal to you.
Test1: Alice takes [1,4], Bonnie takes [3,1]
Test2: Alice takes [4], Bonnie takes [0], stack one remains untouched.
Test3: Alice takes [0], Bonnie takes [10].
In problem F, case a + b < c + d, I still don't understand why we can change the stack to a photo with value (a - d, d - a) if a > d, and (c - b, b - c) if b < c.
I know the reason of a - d and b - c but d - a and c - b seem to be confusing to me.
In the a > d case, this is equivalent to deleting the photo and adding a - d to the final answer. Probably I should have written that in the editorial instead as it would be clearer. The method of substituting a different photo just results in slightly shorter code.
I get it now, thanks!
The proof for problem E was awesome!!