We have N persons numbered from 1 to N. Also there are M identical rooms with infinity capacity.
In how many ways we can distribute persons in rooms such that each room contains at least 1 person ?
Two ways A and B are regarded as the same if for any room in A, there exists a room in B that the persons in these two rooms have the same set of numbers. In other words, rooms are indistinguishable.
for example : 2 rooms , 3 persons , ans = 3 : (1)(2,3) , (2)(1,3) , (3)(1,2)











Pretty sure you're talking about the Stirling numbers of second kind.
thanks so much ...
Now problem is that I have to answer 10^5 queries of this problem when N is same for all queries but M is different for each query from 1..10^5. ( N is in range 1..10^5 )
It seems that this numbers need huge time for calculation , how can we reduce it ? or I am wrong ?
Well the answer to you problem (and the ShareCode problem) is that because N is the same you can calculate these Stirling values using the recursive formula and FFT (NTT to be more specific), the modulo number in that problem was so that you could use NTT.
keyvankhademi, my teammate was the one who solved it, you can ask him for more details ;)
thanks...
congratulations for being the only team who solved it ... :)
Can you please share the link to the original problem? Thanks!
Here
actually you can use this formula
as you can see it can be written as the product of two polynomials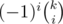 and (k - i)n
and (k - i)n
so you can easily find s(n, k) for a fixed n and all k.
thanks... very nice! congratulations for being the only team who solved it ... :)
I don't know FFT for programming contests yet ... I have to learn it first ... can you suggest a good resource for learning it ?
I was reading your approach and I noticed that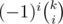 is not a 1-D array that you can easily multiply, it's 2-D so it can't be used. What we can do here is to reformat the formula:
is not a 1-D array that you can easily multiply, it's 2-D so it can't be used. What we can do here is to reformat the formula: 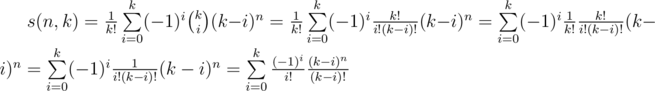 so you should use
so you should use  and
and 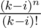 . So if you have two polynomials, one with coefficients
. So if you have two polynomials, one with coefficients 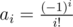 and one with coefficients
and one with coefficients  , then k - th coefficient of their product is indeed s(n, k).
, then k - th coefficient of their product is indeed s(n, k).
P.S: Nice approach by the way, inclusion-exclusion principle...
Each of N persons to any of M rooms minus cases of N persons in M-1 rooms m^n-m*(m-1)^n
My friend , problem is not as easy as you think ... you must make sure that each room contains at least one person. Also notice that all the rooms are same.