Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
| Name |
|---|



Interesting contest. But I think there are solutions more understandable than yours. (For A,B and C problems). Thanks for the contest and sorry for my poor English.
It's a pity that there is no editorial for the only difficult problem.
My solutions:
this round made me sad :(
ignore
that moment when you write sieve's algorithm for problem A, then when writing the main function goes: screw that, I don't need this.
off topic question: at what rating did you go into div1?
I think it's 1900
jajajaja its hapened to me during the contest, i lose likke 2 minutes on thar and like one more in erase that.
I thought I was the only one who did that xD. And wasted a lot of time in it. I was about to give up then I decided not to give up. For the first time solved 3 questions and for the first time solved all of them correctly =) Back to cyan where it all begun
I'm trying to understand the naive solution for problem E.
Is it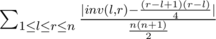 , where inv(l, r) is the number of inversions inside segment [l, r]?
, where inv(l, r) is the number of inversions inside segment [l, r]?
UPD: The correct formula is
No, it is diffeence between inv(1,n) and answer. (Without abs, you shouldn't forget about sign).
Explanation: What happens after shuffle random segment [l,r]? What happens with inversion count in whole permutation. It will be inv(1,n) — inv(l,r) + expected(l,r), where expected(l,r) — is an expected value of inversion count after shuffle. So, all segment equiprobable, than we should calc average among all l, r. And inv(1,n) is a constant so we can just add to your formula (without abs).
I hope you understand me.
I got it! Thanks!
Now I'm trying to understand the optimized solution... I understand that we must fix a left bound, i, from n down to 1, but I can't understand what exactly we should maintain...
The main idea of optimized solution is to process all segments which start in one position together with O(logN) for each start position. Now i'll explain how to calculate sum of inv(l, r) (first value in numerator of your fraction) for each l, rl < = r (second value in numerator can be easily calculated in many ways). Lets answer[i] — sum of inv(i, r) for each r > = i. Now we want to calculate answer[i] and we already had an answer[i + 1] value. answer[i] consists of answer[i + 1] (because segment [i, r] can be splitted to [i, i] and [i + 1, r]) and сount of numbers to the right of which is less than the a[i] (ie which form inverse with a[i]). And the number of positions in the n must be included 1 time (because only [i, n] contains it), the number on the n - 1 position – 2 times (because both [i, n - 1] and [i, n] contains it), etc. Those the number on j position must be included n - j + 1 times. And for that we can maintain a data structure, such as a Fenwick tree (BIT). After processing position j we will add value n - j + 1 to the tree.
Lets look at an example:
we have an array 3 4 2 1
answer[4] = 0
answer[3] = answer[4] + 1 (inv 2-1) = 1
answer[2] = answer[3] + 1 (inv 4-1) + 2 (inv 4-2 included two times because it presents in two segments [2,3] and [2,4] = 4
answer[1] = answer[2] + 1 (inv 3-1) + 2 (inv 3-2 included two times because it presents in two segments [1,3] and [1,3] = 7
So count of inversions amogn each pair l,r equal answer[1] + answer[2] + answer[3] + answer[4] = 14.
You can see my code 23181044 (at the bottom). UPD I've been noticed, that participants can't see my submission, so code available here
Got it!!! Thank you very much!
Isn't answer[1] + answer[2] + answer[3] + answer[4] = 12 ?
Sure, my bad.
why you added (r-l+1)*(r-l)/2 , what is significance of this ?
D problem is also solvable with Paralel Binary Search.
Here is my code 23168802.
Can someone please explain me why does the greedy mentioned in the editorial works for problem C ? I mean I had another greedy approach which was as follows-push all the positions of R and D in two separate queues. Then simulate thorugh both of the queues. If the position at which we currently are isn't already disabled then we disable the first element in the queue with opposite parity. Almost the same thing is mentioned in the editorial but it takes out the current element and pushes it to the back of the queue after adding n to it. What i felt initially was that if I am currently at 'D' I can disable any of the 'R' in the sequence because anyway it's going to come before the current if at all it comes. Why does the choice of the postion of the opposite parity important here? Can anyone please explain me. Thanks in advance :)
ya, same problem please explain
See this case:
RDRDDRD
Here, if the D at position 5 disables the first R, like in your solution, R wins, however, if it disables D at position 6, D wins.
Of course, D would disable R at 6 because they want to win. This order matters because you want to disable maximum number of the opposite who are yet to vote in this turn(and if none are left, start from the beginning). This would enable your votes to be more "continuous" and disable even more of the opposite.
So, you should disable greedily the next person from the opposite who has not been disabled.
Following this strategy, no one would have to vote more than twice, so with input size ≤ 200000, just simulating it will fit easily in the time limit.
another simpler test case
RDRDD
Participated in 5 consecutive contests and haven't reached purple yet :( got WA for one problem each contest
Div2C Can somebody tell why this code 23170947 gives TLE on Codeforces while giving correct output on my computer. I have used Linked list to make groups of R and D initially. Then I simulate the process of voting on each iteration and erase a group from linked list if all of its members are banned. My guess is that erase is somehow changing iterator on Codeforces. I don't know how.
Can anyone help with DIV2D... what is wrong in my solution it is giving TLE in test case no.- 8.... http://ideone.com/wU8cAf or solution no 23172059
because of using loop on vector V inside the query.in worst case query can be n and size of vector is n.so total O(n*n).
You process every query with O (N) complexity, so result, the complexity of your solution is O (QN) and can't fit to TL.
Here's a different approach for div2D with binary search and prefix sum. (When I looked at the problem I thought removing those bids from the bet is a terrible idea as it would take a long time, as I didn't thought to group them by the man who bids would help)
Step 1: Keep a prefix sum of the bidders' id and a list of bid's that each of them have made. We will also assume a bidder with id [0] made the [0 0] bid, so the input will be 1-based.
Step 2: Binary search for the final bid, the middle bid has two cases:
Case 1: It is NOT an abscent bid
Then, for each of the abscent bidders and the one who made the middle bid, binary search to count their bids made after that bid. We will adjust the binary search range depending if the bids made matches all the bids that should be made afterwards.
Case 2: It is an abscent bid
Then, for each of the abscent bidders we retrieve the amount of bids they make. To "guess" the next non-abscent bid, we can make use of the prefix sum of ids. Since if this is a valid segment, then it would consist at most of one-valid bids (or none as the same guy may have bid earlier to cancel out the remainng bid in this segment). By using the prefix sum and the bid counts of each abscent bidders, we can have a possible guess of the non-abscent bidder which we are looking for (Note that we may have got the wrong guy, but if the one and only non-abscent bidder exists, it is guaranteed to find the correct one). We will also retrieve the amount of bids that he made after the middle bid, and adjust the binary search range.
Note that the result is not neccessary the final middle bid, it could possibly be the non-abscent bid we found in case 2, so the result should be kept independently instead of just printing the final middle position.
Code
This is my solution for problem E:
First, count the inversions in the initial permutation. It's a "default" value and now we will see how it changes after shuffle and modify it.
Let's iterate from right to left. So when we are processing an index i, the greater indices are already processed. Suppose a[i] = x, and a[r] = y, where i < r, and x < y. Now numbers x and y doesn't form an inversion. Let's count the number of segments where these numbers can cause an inversion after shuffle. The left end can be any of 0, 1, ..., i. And the right end can be any of the r, r+1, ..., n-1. So for the fixed position r the number of such segments is (i + 1) * (n — r).
To get the total number of segments whose shuffle can lead to the inversion with the element a[i], we need to sum (i + 1) * (n — r) for all r such that a[i] < a[r]. This can be done using a Fenwick tree. After we process an index i, just add (n — i) to the position a[i] in the tree. And to get the sum of all (n — r) ask the tree the sum on segment [a[i], n — 1].
This is how we calculate the total number of segment whose shuffle can lead to increasing the number of inversions. If we get the sum on the segment [0, a[i]] instead of [a[i], n — 1], we get same thing for decreasing the number of inversions.
Now let's attach the probabilities to this solution. For every segment, if it can increase / decrease the number of inversions, it does it with the probability 0.5. Because in the half of all permutations elements a[i] and a[j] appear in increasing order, and in the other half — in decreasing order. So we divide the delta answer by n * (n + 1) / 2 as it's the total number of segments, and then multiply by 0.5 as 0.5 is the probability that any inversion can happen.
My code: http://pastebin.com/mybK6Lkp
why we need to add (n-i) to the position a[i] in the tree.
It is added to keep track of the amount of valid positions for the end of the segment which could cause inversion.
Why my soltion for problem D got TL ?
vector < pii > mx = vec[t[1].S];
Creating vector works O(size)
in div2 C why is it profitable to always remove the second opponent why can't we remove the first unremoved opponent(the one who has already voted) so that in the next round he can't vote against anyone
For problem E, this is how I calculated number of inversions for the example [2 3 1]
[2 3 1] (inv:2)Expected inv: 2[2 3 1] (inv:2)Expected inv: 2[2 3 1] (inv:2)Expected inv: 2[2 3 1] (inv:2)[3 2 1] (inv:2)Expected inv: 2[2 3 1] (inv:2)[2 1 3] (inv:1)Expected inv: 3/2[1 2 3] (inv:0)[1 3 2] (inv:1)[2 1 3] (inv:1)[2 3 1] (inv:2)[3 1 2] (inv:1)[3 2 1] (inv:2)Expected inv: 7/6Since selection of each segment is equiprobable and then each permutation is equiprobable, then the expected number of inversions should be 1/6(2 + 2 + 2 + 2 + 3/2 + 7/6) = 16/9.
This is not equal to the output. Where am I mistaken?
Segment [2] -> 2 3 1 Expected inv: 2
Segment [3] -> 2 3 1 Expected inv: 2
Segment [1] -> 2 3 1 Expected inv: 2
Segment [2 3] -> 2 3 1 3 2 1 Expected inv: (2+3) / 2 = 5/2
Segment [3 1] -> 2 3 1 2 1 3 Expected inv: 3/2
Segment [2 3 1] -> 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 Expected inv: (0+1+1+2+2+3) / 6 = 9/6 = 3/2
Expected inv: 1/6(2+2+2+5/2+3/2+3/2) = 23/12
Another solution for E, using the classical merge sort algorithm to count inversions:
Let I(p) be the number of inversions of a permutation p, a the initial permutation and b the result after the operation. Then E(I(b)) is the sum of P(bi > bj) for all 1 ≤ i < j ≤ n. Therefore we compute for each inversion (i, j) (and for each non-inversion, using the "mirrored permutation") of a the probability that the elements at that position are also an inversion of b.
If (i, j) is an inversion of a, then the probability that ai and aj are still in that order in b is (either we choose a segment not containing i and j, or we do but we don't swap i and j) :
Hence we compute for each i the sum of n - j + 1 for all j such that (i, j) is an inversion of a while we compute the number of inversions.
AC : 23177271
What is C's time complexity? I assume it is O(n), but how to prove it?
It's O(n) indeed. There will be O(n) votes casted, as each vote denies another vote.
If I understand correctly, after each "round", the number of votes is halved. So the overall number of votes <= n /2 + n/4 + ...+ 1 = O(n)?
Instead of considering it round-based, consider the overview situation. Whenever a vote is casted, the amount of people that are eligible to cast a vote reduces by one.
duplicated post.
B seemed to be the hardest problem for me( solved E during the contest — but could not get around B's editorial) :P
Here is my solution without any analysis needed — for each point (x,y) belongs to [-3000,3000] check if it is a candidate(connect it to the rest points in one of 3 ways — the opposite sides should be parallel(simply equal vectors).)
By definition the intersection of diagonals in paralelogram is the midpoint of both diagonals.You can fix one diagonal,find the midpoint and then find the fourth point using the third point and the midpoint.
The midpoint of (x0, y0), (x1, y1) is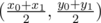 .
.
"Otherwise he should bid the minimal value that is greater than the maximal bid of the second man in the set."
How can we use max bid of second man without doing compression of the bids for each person? After all, we can reduce this max bid of the second man, which will require a lower bid from the winner.
I also thought of that. Nevertheless, suppose that in the bid you are studying, the maximum bid of the second place is c, the minimum bid of the winner greater than c is a, and his next bid is b. You have 2 cases:
b > c: This is a contradiction with the assumption that a > c.
b < c: Notice that the winner cannot win just by bidding b, because then, the second guy will bid c and he will win.
Therefore, regardless of the order and the amount of the bids, the first guy will always win with a bid of a.
erratum? biection -> bijection
Apparently unordered_map.clear() is really slow. Could not figure out why I was getting TLE on D for days and that was the culprit. Anyone know why?
Is there any reason why it shows "Tutorial is not available"? I think 2-3 days ago the tutorials were available. I am practicing previous contest's problems and some of them also shows this. Can anyone explain why? edit: It's back. I guess it's temporary.