Hello, Codeforces!
Recently I stumbled upon a certain problem. Given n pairwise distinct positive integers (let's say all of them are less than or equal to 109), you're ought to find such smallest possible k that these numbers modulo k will still be pairwise distinct.
I'll be thankful if someone suggests a non-naive solution (i.e. w/o explicitly calculating all the pairwise differences) or provides some ideas to start with.











Auto comment: topic has been translated by rek (original revision, translated revision, compare)
For each pair find a positive difference. Find all divisors of that difference — add them to global hash-table. Iterate numbers from 1 to infinity and check presence in hash-table. If it's not in hash-table, that's your k.
If you have pair 1 & 7, difference is 6, divisors are 1,2,3,6 (added to hash-table) — so the smallest k is 4. Keep adding divisors for other pairs and then find smallest k.
Complexity O(n * sqrt(m)), where n — number of pairs and m is 10^9 in your case.
Thank you for your answer! Considering we have n numbers, we would get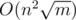 complexity, which is not much better than a naive solution, so I'm still looking for a better way to do this (if there's any).
complexity, which is not much better than a naive solution, so I'm still looking for a better way to do this (if there's any).
Ah, I see n distinct numbers, not n pairs that got distinct numbers.
Is there a constraint on k? Large k will always work
Oh, thank you for this message, I didn't point before that k must be as small as possible. My fault.
Can you please post the link?
Well, to tell the truth, there is no such competitive programming problem anywhere, my friend and I came up with the idea of it some days ago, and we have been looking for the solution for a few days, but we couldn't find anything similar either in archives or in Google, so I can't.
Next time just say that in the beginning, okay?