757A — Gotta Catch Em' All!
Author: Baba
Testers: virus_1010 born2rule
Expected complexity: 
Main idea: Maintain counts of required characters.
Since we are allowed to permute the string in any order to find the maximum occurences of the string "Bulbasaur", we simply keep the count of the letters 'B', 'u', 'l', 'b', 'a', 's', 'r'. Now the string "Bulbasaur" contains 1 'B', 2'u', 1 'l', 2'a', 1 's', 1'r' and 1 'b', thus the answer to the problem is Min(count('B'), count('b'), count('s'), count('r'), count('l'), count('a')/2, count('u')/2). You can maintain the counts using an array.
Corner Cases:
1. Neglecting 'B' and while calculating the answer considering count('b')/2.
2. Considering a letter more than once ( 'a' and 'u' ).
757B — Bash's Big Day
Author: architrai
Testers: mprocks, deepanshugarg
Expected complexity: 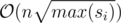
Main idea: Square-root factorization and keeping count of prime factors.
The problem can be simplified to finding a group of Pokemons such that their strengths have a common factor other that 1. We can do this by marking just the prime factors, and the answer will be the maximum count of a prime factor occurring some number of times. The prime numbers of each number can be found out using pre-computed sieve or square-root factorization.
Corner Cases : Since a Pokemon cannot fight with itself (as mentioned in the note), the minimum answer is 1. Thus, even in cases where every subset of the input has gcd equal to 1, the answer will be 1.
757C — Felicity is Coming!
Author: shivamkakkar
Testers: codelegend
Expected complexity: 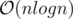
Main idea: Divide pokemon types into equivalence classes based on their counts in each list.
Consider a valid evolution plan f. Let c[p, g] be the number of times Pokemon p appears in gym g. If f(p) = q then 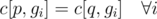 .
.
Now consider a group of Pokemon P such that all of them occur equal number of times in each gym (i.e. for each 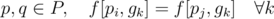 ). Any permutation of this group would be a valid bijection.
). Any permutation of this group would be a valid bijection.
Say we have groups s1, s2, s3, ..., then the answer would be |s1|! |s2|! |s3|! ... mod 109 + 7.
For implementing groups, we can use vector < vector < int > > and for i-th pokemon, add the index of the gym to i-th vector.
Now we need to find which of these vectors are equal. If we have the sorted vector < vector < int > > , we can find equal elements by iterating over it and comparing adjacent elements.
Consider the merge step of merge sort. For a comparison between 2 vectors v1 and v2, we cover at least min(v1.size(), v2.size()) elements. Hence  work is done at each level. There are
work is done at each level. There are 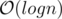 levels.
levels.
Bonus : Try proving the time complexity for quicksort as well.
757D — Felicity's Big Secret Revealed
Author: saatwik27
Testers: imamit,abhinavaggarwal,Chipe1
Expected complexity: 
Main idea: DP with Bitmask.
This problem can be solved using Dynamic Programming with bitmask.
The important thing to note here is that the set of distinct numbers formed will be a maximum of 20 numbers, i.e. from 1 to 20, else it won't fit 75 bits(1*(1 bits) + 2*(2 bits) + 4*(3 bits) + 8*(4 bits) + 5*(5 bits) = 74 bits). So, we can use a bitmask to denote a set of numbers that are included in a set of cuts.
Let's see a Top-Down approach to solve it :
Lets define the function f(i, mask) as : f(i, mask) denotes the number of sets of valid cuts that can be obtained from the state i, mask. The state formation is defined below.
Let M be the maximum number among the numbers in mask. mask denotes a set of numbers that have been generated using some number of cuts, all of them before bi. Out of these cuts, the last cut has been placed just before bi. Now, first we check if the set of cuts obtained from mask is valid or not(in order for a mask to be valid, mask == 2X - 1 where X denotes number of set bits in the mask) and increment the answer accordingly if the mask is valid. And then we also have the option of adding another cut. We can add the next cut just before bx provided the number formed by "bi bi + 1...bx - 1" <= 20. Set the corresponding bit for this number formed to 1 in the mask to obtain newMask and recursively find f(x, newMask).
757E — Bash Plays with Functions
Author: satyam.pandey
Testers: Superty,vmrajas
Expected complexity: 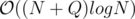
Main idea: Multiplicative Functions.
We can easily see that f0 = 2(number of distinct prime factors of n). We can also see that it is a multiplicative function.
We can also simplify the definition of fr + 1 as:

Since f0 is a multiplicative function, fr + 1 is also a multiplicative function. (by property of multiplicative functions)
For each query, factorize n.
Now, since fr is a multiplicative function, if n can be written as:
Then fr(n) can be computed as:
Now observe that the value of fr(pn) is independent of p, as f0(pn) = 2. It is dependent only on n. So we calculate fr(2x) for all r and x using a simple R * 20 DP as follows:
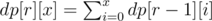
And now we can quickly compute fr(n) for each query as:
757F — Team Rocket Rises Again
Author: Baba
Testers: shubhamvijay, tanmayc25, vmrajas
Expected complexity: 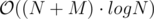
Main idea: Building Dominator tree on shortest path DAG.
First of all, we run Dijkstra's shortest path algorithm from s as the source vertex and construct the shortest path DAG of the given graph. Note that in the shortest path DAG, the length of any path from s to any other node x is equal to the length of the shortest path from s to x in the given graph.
Now, let us analyze what the function f(s, x) means. It will be equal to the number of nodes u such that every path from s to u passes through node x in the shortest path DAG, such that on removing node x from the DAG, there will be no path from s to u.
In other words, we want to find the number of nodes u that are dominated by node x considering s as the sources vertex in the shortest path DAG. This can be calculated by building dominator tree of the shortest path DAG considering s as the source vertex.
A node u is said to dominate a node w wrt source vertex s if all the paths from s to w in the graph must pass through node u.
You can read more about dominator tree here.
Once the dominator tree is formed, the answer for any node x is equal to the number of nodes in the subtree of x in the tree formed.
Another approach for forming dominator tree is by observing that the shortest path directed graph formed is a DAG i.e. acyclic. So suppose we process the nodes of the shortest path dag in topological order and have a dominator tree of all nodes from which we can reach x already formed. Now, for the node x, we look at all the parents p of x in the DAG, and compute their LCA in the dominator tree built till now. We can now attach the node x as a child of the LCA in the tree.
For more details on this approach you can look at jqdai0815's solution here.
757G — Can Bash Save the Day?
Author: Baba
Testers: Toshad, abhinavaggarwal
Expected complexity: 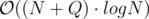
Main idea: Making the Centroid Tree Persistent.
Simpler Problem
First let's try to solve a much simpler problem given as follows.
Question: Given a weighted tree, initially all the nodes of the given tree are inactive. We need to support the following operations fast :
Query v : Report the sum of distances of all active nodes from node v in the given tree.
Activate v : Mark node v to be an active node.
Solution: The above problem can be easily solved by a fairly standard technique called Centroid Decomposition. You can read more about here
Solution Idea
- Each query of the form (L R v) can be divided into two queries of form (1 R v) - (1 L - 1 v). Hence it is sufficient if we can support the following query: (i v) : Report the answer to query (1 i v)
- To answer a single query of the form (i v) we can think of it as what is the sum of distance of all active nodes from node v, if we consider the first i nodes to be active.
- Hence initially if we can preprocess the tree such that we activate nodes from 1 to n and after each update, store a copy of the centroid tree, then for each query (i v) we can lookup the centroid tree corresponding to i, which would have the first i nodes activated, and query for node v in
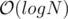 time by looking at it’s ancestors.
time by looking at it’s ancestors. - To store a copy of the centroid tree for each i, we need to make it persistent.
Persistent Centroid Tree : Key Ideas
- Important thing to note is that single update in the centroid tree affects only the ancestors of the node in the tree.
- Since height of the centroid tree is
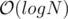 , each update affects only
, each update affects only 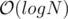 other nodes in the centroid tree.
other nodes in the centroid tree. - The idea is very similar to that of a persistent segment tree BUT unlike segtree, here each node of the centroid tree can have arbitrarily many children and hence simply creating a new copy of the affected nodes would not work because linking them to the children of old copy would take
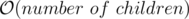 for each affected node and this number could be as large as N, hence it could take
for each affected node and this number could be as large as N, hence it could take 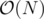 time in total !
time in total !
Binarizing the Input Tree
- To overcome the issue, we convert the given tree T into an equivalent binary tree T' by adding extra dummy nodes such that degree of each node in the transformed tree T' is < = 3, and the number of dummy nodes added is bounded by
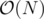 .
. - The dummy nodes are added such that the structure of the tree is preserved and weights of the edges added are set to 0.
- To do this, consider a node x with degree d > 3 and let c1, c2...cd be it's adjacent nodes. Add a new node y and change the edges as follows :
- Delete the edges (x - c3), (x - c4) ... (x - cd) and add the edge (x - y) such that degree of node x reduces to 3 from d.
- Add edges (y - c3), (y - c4) ... (y - cd) such that degree of node y is d - 1. Recursively call the procedure on node y.
- Since degree of node y is d - 1 instead of original degree d of node x, it can be proved that we need to add at most
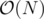 new nodes before degree of each node in the tree is < = 3.
new nodes before degree of each node in the tree is < = 3.
Conclusion
Hence we perform centroid decomposition of this transformed tree T'. The centroid tree formed would have the following properties.
- The height of the centroid tree is
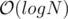
- Each node in the centroid tree has ≤ 3 children.
Now we can easily make this tree persistent by path-copying approach.
To handle the updates,
- Way-1 : Observe that swapping A[i] and A[i + 1] would affect only the i'th persistent centroid tree, which can be rebuilt from the tree of i - 1 by a single update query. In this approach, for each update we add
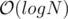 new nodes. See author's code below for more details.
new nodes. See author's code below for more details. - Way-2 : First we go down to the lca of A[x] and A[x + 1] in the x'th persistent tree, updating the values as we go. Now, let cl be the child of lca which is an ancestor of A[x], and let cr be the child which is an ancestor of A[x + 1]. Now, we replace cr of x'th persistent tree with cr of (x + 1)'th persistent tree. Similarly, we replace cl of x + 1'th persistent tree with cl of x'th persistent tree. So now A[x + 1] is active in x'th persistent tree and both A[x] and A[x + 1] are active in (x + 1)'th persistent tree.To deactivate A[x] in x'th persistent tree we replace cl of x'th persistent tree with cl of (x - 1)'th persistent tree. Hence in this approach we do not need to create new
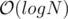 nodes for each update. See testers's code below for more details.
nodes for each update. See testers's code below for more details.
Hope you enjoyed the problemset! Any feedback is appreciated! :)











Auto comment: topic has been updated by Baba (previous revision, new revision, compare).
Auto comment: topic has been updated by Baba (previous revision, new revision, compare).
Thanks for the refreshing problemset!
My only rant is that the first example for problem A could be more trivial, as the problem statement is rather long I just skipped to the example to copy the string, and I fell for the trap.
PS: The link to problem E is broken
A description of a simpler approach to G, that does not require complex data structures and works pretty fast.
approach to G, that does not require complex data structures and works pretty fast.
Let's say that vertex ai is assigned with a key i. Consider the centroid decomposition. Suppose, we have to answer the query of a first type for a vertex v and range [l, r]. Consider all layers of centroid decomposition that contain v: for each layer L with its centroid c we will account all paths from v to some vertex (with key in range [l, r]) that completely belong to the layer L. By the properties of centroid decomposition, all such paths pass through centroid c. Denote as L' the subtree of c that v belongs to (that is the smaller layer of centroid decomposition). So, the sum of lengths of all those paths is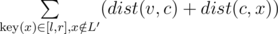 . Here statement
. Here statement 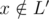 is necessary because the simple path from v to x should pass through c and do not return to the same subtree L'.
is necessary because the simple path from v to x should pass through c and do not return to the same subtree L'.
Let's rewrite this sum as:
where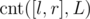 is the number of vertices in layer L whose keys belong to [l, r], and
is the number of vertices in layer L whose keys belong to [l, r], and  is the sum of distances to c in all vertices of layer L with keys from range [l, r].
is the sum of distances to c in all vertices of layer L with keys from range [l, r].
Note that values in both brackets do not depend on v, so we will concentrate on storing them in some data structures in each layer of centroid decomposition in such way that we are able to perform range queries. To ease the computation, on each layer we will take care only of summands that contain L, processing everything with L' when we move to the next layer. Now we need only to be able to find cnt([l, r], L) and sumdist([l, r], c, L).
This can be done by keeping pairs (key(v), dist(v, c)) in some balanced search tree like Cartesian tree, but this is not fast enough (that was what I tried during the contest). Let's exploit the fact that swaps are allowed only for vertices with adjacent keys: in each layer of centroid decomposition store a vector of keys and a vector of prefix sums of values dist(v, c). In order to answer to query [l, r], find the correct range by a binary search and use prefix sums. When we need to swap keys of two vertices ax and ax + 1, it's easy to see that in each affected layer (there are no more than of them, namely, all layers containin ax or ax + 1 are affected) these two vectors are changed in O(1) places.
of them, namely, all layers containin ax or ax + 1 are affected) these two vectors are changed in O(1) places.
That is a sketch of my solution, the implementation may be found here: http://codeforces.com/contest/757/submission/23772311
By the way, nice idea with making centroid decomposition persistent, I liked it! The most impressive part is that when we store persistently copies of our data structure built for each possible prefix of nodes activated, we can still perform adjacent swaps in on-line, I've never seen such an approach before.
I have also never seen an approach like this before :P
For E, I've noticed the following pattern:
fr(pe) =
= r + 2 if e = 1,
= (r + 1)(r + 2)...(r + e - 1) * (r + 2e) / factorial(e) otherwise.
23786556
Some (maybe useful) theory which comes with problem E:
Given two functions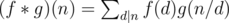 .
.
f,g : N -> Nwe can define it's Dirichlet convolution asWe can check that if
f,gare multiplicative then so isf * g.In fact
f_rfrom the statement is just1*1*...*1*f_0where 1 means constant function equal to one.Another thing to know is that to a function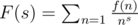 . It is nice because if
. It is nice because if
f: N -> Nwe can attach a generating functionf,gcoressponds toF,Gthenf * gcoressponds toFG. Moreover when the functionfis multiplicative we can writeThis is so-called Euler product.
Let us focus on this
1*1*...*1. The function 1 corresponds to the celebrated zeta functionso
1*1*...*1corresponds to r-th power of zeta. Let us use the Euler product to compute this we haveNow it is not hard to see that the function
F_0corresponding tof_0is justFinally
therefore
and from multiplcativity we are done.
Building dominator tree is not necessary in problem F. We can just compute the highest dominator which is not s for every node of the DAG. Define the highest dominator of node x which is not s as hdom(x). Process the nodes of the DAG in topological order. If node x has s as its parent in the DAG then hdom(x) = x. Otherwise if for some y, hdom(p) = y for all parents p of node x then hdom(x) = y. Otherwise hdom(x) = x.
Now the answer is the node which is the highest dominator for the most of the nodes. Code: 23783649
In fact you can just do topological sort on the shortest path DAG formed in F (maybe we are doing same thing? but it's linear) 23787847
Edit: basically same idea with Laakeri
Someone can explain in E why f is multiplicative?
It's a well known result in number theory. If g is defined by: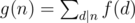 , then if f is multiplicative g is also multiplicative. Proof: Let n, m be integers with
, then if f is multiplicative g is also multiplicative. Proof: Let n, m be integers with 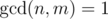 , then
, then 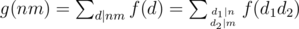 . Here gcd(d1, d2) = 1 and then
. Here gcd(d1, d2) = 1 and then 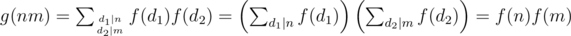 . Btw the reciprocal is also true, if g is multiplicative then f is also multiplicative.
. Btw the reciprocal is also true, if g is multiplicative then f is also multiplicative.
if n = p1^q1*p2^q2*...*pm^qm f0(n) = 2^m is multiplicative. fr = f(r-1) * 1 , * means Dirichlet convolution. One can prove that if f and g is multiplicative then f*g is multiplicative. So fr(n) is multiplicative.
Problem A and B were good for first problems of div1+div2 contest, but other problems were really hard. Congrats to winners!
Could anybody explain B please?
any puzzle?
The guy Maun_Zhu hasn't worked Problem B out yet~~~ Never believe him!
The guy Real_EnderDragon has the rating down,don't trust him!!
But I worked Problem B out. There is no need to argue with a guy whose rating is higher than you my friend. The reason I why has my rating down was just that I played Hearthstone when I had no consideration about the problem. In my country it was at 1:00 am and I was tired. Even did I lose 4 games. What sad news.
Wow, solution to G is very nice :). Kinda coding-heavy, but I think ideas are pretty innovative. Rather impossible to code such solution during contest, but I am happy it was not next problem like "pretty obvious what to do, just apply HLD and LinkCut to suffix tree" :P.
For question D, the analysis is not that straightforward. (Admission: I TLE'd in one submission due to a worse implementation of the dp that didn't stop after num>=20, as in the author's code, and passed with a random distance heuristic)
Purely from a naive analysis, we have N*2^20 states, each of which requires a while loop. If all digits are 0, for example, then the while loop runs up to 75 times. So this is O(N^2*2^20).
However, having many consecutive 0s actually reduces the number of states called by the recursion and probably makes it run faster instead.
Also, there is a hidden factor of lg 20 (while loop runs lg 20 times "on average").
On the flip side, not all 75*2^20 states can be called.
Does anyone know whether the analysis can be made tighter that O(NlgN*2^20)?
I also wonder how the author can claim N*2^20 directly when a single state calculation takes O(N) time. I had a different dp solution having runtime of N*10*2^20: 23765830
Edit: The author's solution is O(N*5*2^20) due to skipping leading zeroes.
The author's solution doesn't take O(N) time to calculate a single state. It takes atmost 5 steps. Although, the code can be made faster(due to simplification of the operations involved) by precomputing the numbers produced from those steps, as pointed out by Zlobober.
But, your solution takes 10 steps to calculate a single state. Moreover, you can check the execution time of my submission here : 23795130.
I think you missed out the following part in my code:
This makes sure that I don't take O(N) due to the leading zeroes.
PS: I didn't see your solution properly before writing the above line about your solution taking 10 steps per state. But, my main point was about the above line that you probably missed in my code.
Thanks. I missed this trick during contest, and wasted an extra hour trying to optimize my dp. Really nice trick and explanation.
From each position i there are actually only at most 5 transitions that correspond to the numbers in range [1, 20], you may easilly precompute all those transitions from each position and iterate only over them.
This solution makes about 75·5·220 ≈ 4·108 very simple operations. You may also make it faster by writing DP in forward direction and pruning the unreachable states, i. e. do not performing transitions from states whose DP value is zero. But in fact the last optimization was not really needed.
Was it possible to solve 757C - Felicity is Coming! using hashing? I tried different p and M in my hash-function, but it gets WA41 or WA42
Use several (at least 2) different modulos and it will pass.
Or do not use a polynomial hashing at all (since you do not need anything like substrings hashes in this problem). Xoring with large random numbers works pretty well here.
Suppose you have a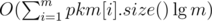 . This equals
. This equals 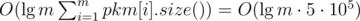 , which fits the time limit. I wonder if all these people using hashes noticed that.
, which fits the time limit. I wonder if all these people using hashes noticed that.
vector<pair<int,int>>for each pokémon type. They're sorted and each pair is of the form (gym, cnt). If you group pokémons by they're "signature" vector using amap<vector<pair<int,int>>,int>, it'll costExcept when anta is in your room.
I think I have got a O(n) method to solve problem B: We can easily see that the final gcd must be a prime. We can just enumerate all the primes less than max(si) and enumerate its multiples to update the ans . According to pi(x)=n/logn and harmonic series the final time complexity is about O(n)
Here is my code http://codeforces.com/contest/757/submission/23782887
In the problem setter's code for D, why don't we add the number represented by bi bi+1 ... bn to the mask before checking if the mask is valid or not?
Edit: NVM, I didn't read the question correctly (idiot).
http://codeforces.com/contest/757/submission/23749033. I have submitted the following code during contest for A but I am getting Time Limit Exceeded on test 56.My code is same as the solution above and matches with tester's code
I don't really know C very well, but I think the strlen() call might be the problem, I believe it is O(n) for every call and thus your code becomes O(n^2) and times out, here is a link for reference.
instead of writing strlen in the loop, assign any new variable the value of strlen, and then substitute strlen for this variable(you should do this,because every iteration in the cycle you call strlen function and the comlexity of your program inceases to O(n^2))
is not a good idea.
This cycle has O(n^2) complexity.
In problem B why does counting the max number of factors give the correct answer?
My solution 23808151 for the problem E does not depend on multiplicative property of function f0(n) and works for any function f0(n) that depends only from the number of primes in factorization of n.
What is your time complexity? I was the tester of this problem. I had a solution in O((time for factorization) + 2(number of prime factors)) per query (after precomputation) which also works (like yours) for any f0 that depends only on number of primes. But it did not pass in these constraints.
what's the idea?
Sorry for the late reply.
Let's say:
For now, $f_0$ can be anything.
Note that you can keep expanding by replacing fr - 1 with fr - 2, etc. Finally we will have:
Now how do we calculate $a_d$?
We can visualize the first equation as follows. We starting with a number n, and we have to make r moves. In a move, if we have n, we can divide it by any number and get d, a divisor of n. After r moves, say we have a number x. Then we add f0(x) to the answer.
We have to consider all possible sequences of moves and add to answer for all of them. So basically for each divisor d of n, we need to find out how many sequences of moves there are from n to d. That will be ad.
let
We can find that ad will be h(r, e1) * h(r, e2) * ... * h(r, eq), where h(r, n) is the number of ways of distributing n of the same prime into r distinct moves.
The overall complexity is O((time for factorizing n) + (number of distinct prime factors of n) * (number of divisors of n)), or around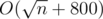 per query.
per query.
All this till here works for any function f0 if fr satisfies the given recurrance.
You can see the code here: https://ideone.com/KHMSAs
If we further have that f0 is a function of the number of distinct prime factors of n, we could perform a further optimization by grouping together divisors having the same set of prime factors. There are at most 7 distinct prime factors for these constraints, so there are at most 128 distinct sets of prime factors. Calculate for each of these. So overall complexity would be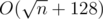 per query, a slight improvement.
per query, a slight improvement.
You can see the optimized version here: https://ideone.com/7TEWih
In problem C , getting WA on test 74 !! Stored all gym no. for each pokemon type in arralists and sorted ! Solution similar to that of tourist's ! http://codeforces.com/contest/757/submission/23807513 http://codeforces.com/contest/757/submission/23747486
Hi, here is a question about 747F's test3. Given 2 cities connected by 1 road. As Bash lives in city1, the only answer could be destroying city2. But Jury's answer is destroying city1. Isn't that wrong? It makes me confused.
You have to output the number of cities that can be disconnected by destroying 1 city + 1(for the destroyed city), not the city to be destroyed.
Hence in test3, we destroy city 2, and hence 1 friend is unhappy.
Can someone find the mistake in my code for C. I am getting WA on test 31. Code: http://codeforces.com/contest/757/submission/23944798