how to prove space complexity in segment tree is O(4*n).
Please subscribe to the official Codeforces channel in Telegram via the link https://t.me/codeforces_official.
×
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/21/2024 15:10:23 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Segment tree with 2^x leaf nodes will have 2^(x+1) — 1 total nodes because it is a perfect binary tree.
Now, you will have useless leaf nodes if you are using general n. Therefore at worst you will have almost 2*n leaf nodes because you must round up to the next power of two. If n is 2^j + 1, then you must have 2^(j+1) leaf nodes = O(2*n).
And as we proved before total nodes is ~2 * leaf nodes so we have 2*2*n = O(4n) total space.
thanks for explanation. is there any other mathematical proof to prove this?
If you're not satisfied by the above proof here is another:
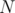 nodes
nodes 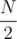 nodes
nodes

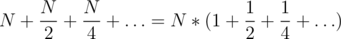 nodes.
nodes. 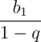 , where
, where  is first element of progression (
is first element of progression ( here) and
here) and 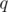 is ratio between two adjacent elements (
is ratio between two adjacent elements ( here).
here). 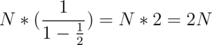 nodes in a segment tree.
nodes in a segment tree.
Last layer:
Pre-last layer:
So, we have
You can see the infinite geometric progression on the right. Its sum is equal to
So, there is a total of
why would it be infinite G.P. on RHS? I mean it could be finite as well right?
This problem was one of the INOI 2012-2013 problems.
At first note that we need exactly 2·n - 1 nodes, but if we use arrays and set id of left child of node with id Id to 2·Id and 2·Id + 1 id to right one, we need an array with size 4·n, let's prove.
Let f(n) the maximum id that we need in segment tree. Let's prove f(2n + 1) = 4·2n - 1. We can prove it using induction, f(21 + 1) = 7, f(2n + 1) = 2·f(2n - 1 + 1) + 1 = 2·(4·2n - 1 - 1) + 1 = 4·2n - 1.
Edit: Definition of f(n) has changed.
Let k be the smallest natural number such that 2k ≥ n. Note that 2k < 2 × n. We will find the answer for 2k. The segment tree, and indeed any other binary tree formed will have exactly k + 1 levels, the i-th containing 2i nodes. Then, the total number of nodes will be a geometric progression of the form 20 + 21 + 22 + ... + 2k, which is precisely equal to 2k + 1 - 1. Since 2k < 2 * n, it follows immediately that 2k + 1 - 1 < 4 × n, so the number of nodes of the new tree — greater than our answer — is still less than 4 × n.
Non-recursive segment trees use exactly 2n - 1 nodes.
@AI.Cash: I've read u non-recursive segment tree. It's very easy, powerful as general segment-tree and required less memory space. But, in non-recursive segment tree how to find lower bound of position for given sum ?? // for perfect binary tree (i.e. n = 2^k):
when n = 2^k, this works fine, but n != 2^k not.
Indeed, for n ≠ 2k we basically get not one tree but O(logn) separate perfect trees. So, it doesn't support the techniques where we need to start from the root and move to the leaves, like binary search and fractional cascading.
Thx. I'll use O(4n) case with your implementation in this case.