798A - Mike and palindrome
Let cnt be the number of 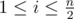 such that si ≠ sn - i + 1.
such that si ≠ sn - i + 1.
If cnt ≥ 2 then the answer is NO since we must change more than 1 character.
If cnt = 1 then the answer is YES.
If cnt = 0 and n is odd answer is YES since we can change the character in the middle, otherwise if n is even the answer is NO because we must change at least one character.
Complexity is O(|s|).
Solution: Link
798B - Mike and strings
First of all, you must notice that the operation of removing the first character and appending it to the left is equivalent to cyclically shifting the string one position to the left.
Let's denote by dpi, j the smallest number of operations for making the first i strings equal to string si moved j times.
Let f(i, j) be the the string si moved j times,then 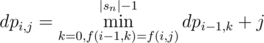 .
.
The answer is min(dpn, 0, dpn, 1, ..., dpn, |sn| - 1).
The complexity is O(|S|3 × n).
Solution: Link
798C - Mike and gcd problem
First of all, the answer is always YES.
If 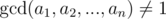 then the answer is 0.
then the answer is 0.
Now suppose that the gcd of the sequence is 1. After we perform one operation on ai and ai + 1, the new gcd d must satisfy d|ai - ai + 1 and d|ai + ai + 1  d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
Using the above observations we can conclude that 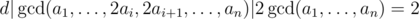 , so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
, so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
Given a sequence v1, v2, ... , vn of zero or one,in one move we can change numbers vi, vi + 1 with 2 numbers equal to 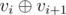 . Find the minimal number of moves to make the whole sequence equal to 0.
. Find the minimal number of moves to make the whole sequence equal to 0.
It can be proved that it is optimal to solve the task for consecutive ones independently so we divide the array into the minimal number of subarrays full of ones, if their lengths are s1, s2, ... , st,the answer is 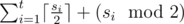 .
.
Complexity is 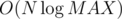 .
.
Solution: Link
798D - Mike and distribution
In the beginning, it's quite easy to notice that the condition " 2·(ap1 + ... + apk) is greater than the sum of all elements in A " is equivalent to " ap1 + ... + apk is greater than the sum of the remaining elements in A ".
Now, let's store an array of indices C with Ci = i and then sort it in decreasing order according to array A, that is we must have ACi ≥ ACi + 1.
Our answer will always have size 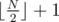 . First suppose that N is odd. Add the first index to our set, that is make p1 = C1. Now, for the remaining elements, we will consider them consecutively in pairs. Suppose we are at the moment inspecting AC2k and AC2k + 1. If BC2k ≥ BC2k + 1 we make pk + 1 = C2k, else we make pk + 1 = C2k + 1.
. First suppose that N is odd. Add the first index to our set, that is make p1 = C1. Now, for the remaining elements, we will consider them consecutively in pairs. Suppose we are at the moment inspecting AC2k and AC2k + 1. If BC2k ≥ BC2k + 1 we make pk + 1 = C2k, else we make pk + 1 = C2k + 1.
Why does this subset work? Well, it satisfies the condition for B because each time for consecutive non-intersecting pairs of elements we select the bigger one, and we also add BC1 to the set, so in the end the sum of the selected elements will be bigger than the sum of the remaining ones.
It also satisfies the condition for A, because Ap1 is equal or greater than the complement element of p2 (that is — the index which we could've selected instead of p2 from the above procedure — if we selected C2k then it would be C2k + 1 and vice-versa). Similarly Ap2 is greater than the complement of p3 and so on. In the end we also add the last element from the last pair and this makes the sum of the chosen subset strictly bigger than the sum of the remaining elements.
The case when N is even can be done exactly the same as when N is odd, we just pick the last remaining index in the end.
The complexity is  .
.
Solution: Link
798E - Mike and code of a permutation
Let's consider ai = n + 1 instead of ai = - 1. Let's also define the sequence b, where bi = j such that aj = i or bi = n + 1 if there is no such j. Lets make a directed graph with vertices be the indices of the permutation p with edges of type (a, b) representing that pa > pb. If we topologically sort this graph then we can come up with a possible permutation: if S is the topologically sorted graph then we can assign to pSi number i.
In this problem we will use this implementation of topological sort.
But how we can find the edges? First of all there are edges of the form (i, bi) if bi ≠ n + 1 .For a vertex i he visited all the unmarked vertices j (1 ≤ j < ai, j ≠ i) and you know for sure that for all these j, pj < pi. But how we can check if j was already marked? The vertex j will become marked after turn of vertex bj or will never become unmarked if bj = n + 1. So there is a direct edge from i to j if j = bi or 1 ≤ j < ai, j ≠ i and bj > i.
Suppose we already visited a set of vertices and for every visited vertex node we assigned to bnode value 0 (for simplicity just to forget about all visited vertices) and now we want to find quickly for a fixed vertex i an unvisited vertex j with condition that there is edge (i, j) or say it there isn't such j, if we can do that in subquadratic time then the task is solved. As stated above the first condition is j = bi if 1 ≤ bi ≤ n, this condition is easy to check. The second condition is 1 ≤ j < ai and bj > i, now consider vertices with indices from interval 1..ai - 1 and take j with maximal bj. If bj > i we found edge (i, j) otherwise there are no remaining edges. We can find such vertex j using segment tree and updating values while we visit a new vertex. In total we will visit n vertices and query the segment tree at most 2 × (n - 1) times (n - 1 for every new vertex and n - 1 for finding that there aren't remaining edges).
Complexity and memory are  and O(N).
and O(N).
Solution: Link










For D, is this magic? 26557143
It was pure intuition xD. I didn't expect such a stupid solution to pass. If someone knows why the probability of choosing a correct solution is sufficiently high, I would be glad to know.
I would be glad to know too because I was so surprised about such a nice solution :D
There is a similar Problem which really need randomized algorithm. http://codeforces.com/problemset/problem/364/D
Maybe the similar of both problem is half of the array
I got the same solution to pass 26559070.
That was a sick try to prove a solution. This proof doesn't work even for 1 array, because "opposite" subset exists only if we forget about cases, where sum of the subset and the rest part are equal. And of course we can't just multiply probabilities because 2 arrays are depending on each other.
By the way, on random tests with n=10000 it takes less than 10 times shuffling.
I solved this problem in same solution. (26557462)
I think the worst case is:
2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 (This is an example of n=20)
In this case, the program must choose n/4 elements in left-half, and n/4 elements in right-half.
So, probability of choose successfully is C(n/2, n/4) * C(n/2, n/4) / C(n, n/2) ≒ 1/sqrt(n).
In summary, you can solve this problem with randomize algorithm in O(n^1.5).
Got AC doing the same and have no idea why it works haha
I don't even know how to make difficult input cases.
how to approximate the probability of not getting a valid subset while taking one randomly?
Is there non-trivial sequences where the answer is unique?
questions I would like to answer haha
The problem B's ideone solution is runtime error.
Oh I have a solution with Ahocorasick automanta,it can be accepted and I think maybe except for the long length of the code,it can be came up with more simply.This is my submission QWQ
And I find a truth that bruteforce can AC and maybe better than AC automanta...QWQFORCE
Can someone please explain the proof for Array 'A' in Problem D?
It's proof is quite unclear to me.
Thanks in advance.
Nevermind what I wrote, I thought you were referring to problem A.
Nice Explanation, but I asked the proof for Problem D. You explained for problem A.
I meant proof of 'Array A' in Problem D.
Once again, you have an array of indices. You sort it by ai in nonincreasing order. Next you will take the first index C1 (aC1 is the biggest). Afterwards you will take one from 2-nd or 3-rd, one from 4-th or 5-th, etc... There might be one index left in case n was even, you will take it as well. You will always satisfy "a-condition" choosing indices that way. Because:
aC1 ≥ any(aC2,aC3);
any(aC2,aC3) ≥ any(aC4,aC5);
any(aC5,aC6) ≥ any(aC7,aC8);
...
| any(aCn — 1,aCn) > 0; — if n is odd
| aCn > 0; — if n is even
You may take any choice between aC2k and aC2k+1, the sum of a-s on the left side will be always greater than the sum of a-s on the right side. Notice strict inequality sign > in the last statement.
Now think about b-s. Simply among C2k and C2k+1 choose one with the biggest b. You will have:
bC1 > 0;
max(bC2,bC3) ≥ min(bC2,bC3);
max(bC4,bC5) ≥ min(bC4,bC5);
...
| max(bCn — 1,bCn) ≥ min(bCn — 1,bCn); — if n is odd
| bCn > 0; — if n is even
Same considerations for b-s. Sum of the left side will be always greater than sum of the right side.
Could you explain, why quite similar greedy doesn't work: 26568197
the idea is: let's sort the first array of pair according to the first element, than create its copy with changed fields and sort the second array according to the second element.
Then reverse both of them.
Take two pointers.
The number of steps is a constant.
Iterate steps. If a step is even, choose the best from the first array and insert to the "answer"-set. if it is already there, increase the pointer until finding unused pair.
Otherwise, if a step is odd, do the same with the second array.
All the test, breaking this solution, are too big and I can't check them.
Try reversing the order on even take best from second array and on odd take best from first array.you will get wa on pretest1
Can someone please explain the bold part: Problem 798C — Mike and gcd problem: Now suppose that the gcd of the sequence is 1. After we perform one operation on ai and ai + 1, the new gcd d must satisfy d|ai - ai + 1 and d|ai + ai + 1 => d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
If you have d|x and d|y, then it's not hard to see that d|x + y and d|x - y also holds (just use the basic definition of definition of divisibility). Now just replace x with ai - ai + 1 and y with ai + ai + 1.
Also, if d|a and d|b, we also have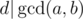 . This comes from the properties of
. This comes from the properties of 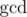 , you should probably google it
, you should probably google it
Using the above observations we can conclude that d | gcd(a1, ..., 2 * a[i], 2 * a[i + 1], ..., a[n]) | 2 * gcd(a[1], ... a[n]) = 2 so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
I don't understand why d | 2 * gcd(a[1], ... a[n]) and why "the gcd of the sequence can become at most 2 times bigger after an operation"
Thank you, I got it.
No,if we choose d=15 and x=3 and b=5 then although 15 is divisible by 3 and 5 both but not by 5+3=8,neither by their difference 2.Will you please explain!
dude its not d thats divisible by x or y .... its the other way round'''
example d=3; x=15, y=9
d|x and d|y
so d|(x+y)
can somebody please explain what does this statement mean in the editorial of C Using the above observations we can conclude that , so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even.
My observation was this. Let's take any two consecutive numbers a1, a2. Let us assume that we are trying to make gcd k which is an odd number. So a1 = k * x1 + r1, a2 = k * x2 + r2. Now a1 — a2 will be a multiple of k if r1 = r2. a1 + a2 will be a multiple of k if r1 + r2 = k. If k is an odd number, it is impossible that r1 = r2 and r1 + r2 = k. Hence we can conclude that you can never try to make gcd an odd number. So we have to aim for making gcd even. That means you need to make the numbers even. That will be enough to make gcd an even number (which will atleast be 2).
Now let's take a1, a2. In two steps, (a1, a2) = > (a1 — a2, a1 + a2) = > (-2 * a2, 2 * a1). So in two steps, any two numbers will be a multiple of 2. So find all consecutive odd numbers. Let this be cnt. Add cnt / 2 to final answer if cnt is even. Add cnt / 2 + 2 to final ans if cnt is odd. If both numbers are odd, only 1 step is needed. If one of them is odd, two steps are needed.
Found your explanation more easy to understand than the editorial. Thanks. Can anyone explain the following statement taken from the tutorial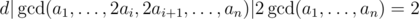
I understand that d divides gcd(a1,...2ai,2ai+1,...an) after operation on ai and ai+1 but why gcd(a1,...2ai,2ai+1,...an) divides 2*gcd(a1,...an)?
https://codeforces.com/blog/entry/51652?#comment-355809
How to solve C using DP ?
hey you can checkout my solution http://codeforces.com/contest/798/submission/26676645
The test data of Problem D maybe too weak? I just used sort and slides to Get AC. In contest, I just fogot the length of this is [n/2]+1
WA32: 26560156 After contest, I just do r+1, then I got AC
AC: 26571236 Could someone prove my idea is correct?
UPD1: I delete sort also got AC.. The algorithm complexity is O(n) 26571390
UPD2: I can prove it now xD
can someone please explain
Given a sequence v1, v2, ... , vn of zero or one,in one move we can change numbers vi, vi + 1 with 2 numbers equal to . Find the minimal number of moves to make the whole sequence equal to 0.in problem C?
Basically since we're trying to make every number a multiple of 2 we're only concerned about the parity of each number so we convert them to zeros and ones by taking ai mod 2. Then we do the moves on this array and try to make them all zero, which is even parity.
Also note that on array v1, ..., vn each move is equivalent to vi xor vi + 1 since we're only concerned about the parity.
Anyone finds C div 2 hard ? Or it is just me
In C, sorry to tell that I just couldn't understand how to translate these mathematical language, could anyone please tell me the meaning in plain english?
What's more, the 't' here confused me, too.
UPD1:now I understand the 't', so stupid am I. XD
Why do we need dp in B? Here is a simple solution - , the
, the 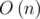 average case!
average case!
First fix a si, we will try to make all other sj equal to si.
We can find the number of shifts needed efficiently by C++ STL function:
(s[j] + s[j]).find(s[i])Sum the total number of shifts needed, repeat this for all si, minimize the number of total shifts needed.
Complexity:
find()function works inCode: 26543372
hi, I saw ur code and I think you assumed that for minimum moves the string to which other strings have to move lies among the given string (in unrotated state ) can you correct me if I am wrong ? you take i th string and check cnt of rotations other strings have to undergo to match this i th string , but what if they have to match i th string rotated twice ?
I am not assuming that! That will happen always!
Let me give an example!
s[j] = cdabands[i] = abcd. We need to rotates[j]to makes[i].I am not assuming that
s[i]is contained ins[j]but surely it will be ins[j]+s[j].s[j] + s[j] = cdabcdaband first occurrence ofs[i]appears in position 2. Se we need 2 shifts! To makes[j],s[i].Just think about it! You will get why this works!
just to confirm, are u saying that answer is always one among given strings (if all strings are valid) ? thanks for reply
Yes! The base string will always be one among given strings :) Because we are not allowed to shift right, only shift left. So it will not be optimal if we shift one left and then try to make all other equal to this! it will be optimal not shifting the base!
So the base string is always from one of the given strings :) Hope it helps :)
I'm not sure for the correctness(At least I passed the tests), but may problem B and C be done in an easier way?
problem B can be achieved in O(nS^2) just by Bruteforce. 26550167
And problem C can be done with linear DP(define f[i][0/1] represents the minimum operation number needed to make the sequence a[1...i-1] all even and leave a[i] even/odd). 26561463
In problem C my approach was first you can take gcd of all numbers and check whether it is greater than 1. If not then you can greedily check for no of moves required to make all ones by using the property that when there are two odd numbers then you can make them even in one move else if there is one odd and one even then you require two moves.
Time complexity: O(n)
Submission link: http://codeforces.com/contest/798/submission/26564933
Yeap, our solutions are quite close, basicly the same idea.
WOW, almost the same idea, I had just finished it! XD code
For problem D what should be the answer for below case? I guess its not possible to choose a subset! Thanks in advance.
2
1 3
But some accepted solution give output
Its wrong I guess!
Surprisingly dreamoon_love_AA's AC solution gives
It is obviously wrong!!
I think you meant to run this case
Yea. Sorry. That was my mistake.
can someone explain why d | gcd(a1, a2, ...., 2ai, 2(ai+1), ....an) | 2*gcd(a1,....an) = 2? I get the first step and the last step. but i don't quite see why gcd(a1, a2, ...., 2ai, 2(ai+1), ....an) | 2*gcd(a1,....an)
don't know ++
I haven`t read all the below comments (might possible , anybody has already mentioned what I will tell ) so spare me if you feel I have wasted your time .
I just want to request I_Love_Tina to kindly once again go through the solution of C problem . Your solution is absolutely correct but I believe you have done a minor mistake while writing editorial . The formula written for calculating answer should have
2 * (si % 2)rather thansi % 2.I can explain that by a simple test case .
for n = 3 and a = {1 , 1 , 1} it will take 3 steps .
Steps are {0 , 2 , 1} {0 , 1 , 3} {0 , 4 , -2}
The above written formula is possibly ignoring the last step . Note :- si means ith element of vector s (as given i is the subscript) .
That's what the ceiling function is for in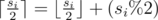
Oh ! Is that ceil function ?? I thought its greatest integer function (floor) .
If that is so , there is no problem .
yes :)
ceil: ⌈x⌉
floor: ⌊x⌋
Oh.. Okay.. Thanks yassin_.. I didn't know that..
I can't understand the editorial for E, can someone help me? I don't understand the described construction and it doesn't seem to correspond to the code...
How do you do toposort with O(n^2) edges in less time?
Obv. my submission which constructs the graph first and then does toposort got TLE (and could also MLE) 26580802
Here.
I had the same question and finally I realized three keys:
The edges are saved in a compact form, i.e. vector a and vector b. To know if there is an edge (i, j), we can check the rules as described in the editorial. The memory requirement is O(N).
Vector b is kept updating while doing toposort. The goal is to avoid checking all the edges (otherwise it takes O(N^2) time). The idea is that if a vertex v is processed while doing toposort, then we can remove all the edges connecting to it. Doing this is simple: set b_v to 0 (and also update the segment tree).
Segment tree is used for efficiently query an unprocessed child node.
Hope this helps.
Yes, thank you for this intuition behind solution :)
Please someone help me on E. I could not get its algorithm in editorial.
I updated the editorial and added some links to the editorial in the code, hope it will help, sorry i'm but bad at explanations :(.
Nice problem. Thank you very much
I have a question for problem D. I understand this "_If BC2k ≥ BC2k + 1 we make pk + 1 = C2k, else we make pk + 1 = C2k + 1_" , but how to prove that sum of all Acpi (let's say S) is greater than (sum of all a[i])-S.
Thanks for the editorial.
In problem E:
'So there is a direct edge from i to j if j = a_i or 1 ≤ j < a_i, j ≠ i and b_j > i.'
I think it should be 'i = a_j' (or 'j = b_i') to match the definition of a and b.
According to writer's code it's j = bi。 And what is even more .... is\n " Lets make a directed graph with vertices be the indices of the permutation p with edges of type (a, b) representing that pa < pb " According to writer's code SHOULD BE "Lets make a directed graph with vertices be the indices of the permutation p with edges of type (a, b) representing that pb < pa"
Fixed.
thanks
by the way,is it possible that the solution will decrease to O(n^2) if it check's every edge?
Yes.
thanks for your amazing problem and patient explantion.:)
In
"But how we can find the edges? First of all there are edges of the form (bi, i) if bi ≠ n + 1"
shouldn't it be
"(i, bi) if bi ≠ n + 1" ?
Really decent/wonderful solution for E! I really love this problem and solution. Thank you for preparing this awesome problem!
For problem C, the editorial states:
It can be proved that it is optimal to solve the task for consecutive ones independentlyIs anyone able to explain this proof? I cannot seem to understand why this is true.
Suppose for k consecutive ones the answer will be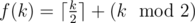 . Now i claim that it isn't optimal to make one subarray full of one out of two. Suppose we have two subarrays of length a, b and distance c(c > 0) between them. It is needed exacty c operations to transform it into one subarray. Then we need to just check if c + f(a + b + c) < f(a) + f(b), it turns out that for c > 1 the inequality isn't satisfied while for c = 1 you can check 3 cases (each parity for a, b) and also verify that it isn't satisfied.
. Now i claim that it isn't optimal to make one subarray full of one out of two. Suppose we have two subarrays of length a, b and distance c(c > 0) between them. It is needed exacty c operations to transform it into one subarray. Then we need to just check if c + f(a + b + c) < f(a) + f(b), it turns out that for c > 1 the inequality isn't satisfied while for c = 1 you can check 3 cases (each parity for a, b) and also verify that it isn't satisfied.
Can someone please explain how choosing just the j with maximal bj work in Problem E, instead of the obvious and inefficient way of choosing all the j(s) satisfying the second condition?
How to prove the greedy part of problem C: that it is optimal to deal with consecutive odd numbers first and then deal with all the remaining odd numbers. This was the difficult part of the proof, which the author of the editorial quite conveniently skips.
Hey. Why in problem C 789C - Functions again if $$$d \mid a_i - a_{i+1}$$$ and $$$d \mid a_{i+1} + a_i$$$ then $$$d \mid 2a_i$$$ and $$$d \mid 2a_{i+1}$$$?
I saw this blog in the recent actions and after looking at the author's username, sorry but only 1 question popped up in my head. I_Love_Tina, does Tina love you?!
Regarding Task-C, the following is written in the editorial
Can someone give a hint of this proof?