hloya_ygrt's blog

Codeforces Round #415 Editorial
By hloya_ygrt, history, 7 years ago, translation, In English
Tutorial is loading...
Setter's code

First accepted Zhigan.

Tutorial is loading...
Setter's code

First accepted polygonia.

Tutorial is loading...
Setter's code

First accepted div2: RaidenEi.

First accepted div1: Lewin.

Tutorial is loading...
Setter's code

First accepted div2: polygonia.

First accepted div1: V--o_o--V.

Tutorial is loading...
Setter's code

First accepted div2: xsup.

First accepted div1: anta.

Tutorial is loading...
Setter's code

First accepted: ksun48.

Tutorial is loading...
Setter's code

First accepted: radoslav11.

  • Vote: I like it
  • +60
  • Vote: I do not like it

Comments Comments (59)
| Write comment?
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

O(1) solution is possible for 810A. Link

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

it's good to mention the First accepted

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

In "809 A — Do you want a date?", the last line of explanation says 2**(i-1) * 2**(n-i-1). I believe it should be (2**i - 1) * (2**(n-i) - 1), i.e. make sure at least one of [1, i] gets picked, and at least one of [i+1,n] gets picked.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Those subsets are allowed to be empty.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      x[i+1] - x[i] is added to final answer for all those subsets where there is at least one integer picked from [1,i] and at least one integer picked from [i+1,n]. Note the closed intervals, and the fact that the implementation of the solution is doing what I described.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yea, you are right, I will fix editorial soon.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh, OK. I misinterpreted the ranges you were considering.

        → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it
    • "They are adding to the answer xi — xi+1 in all the subsets, in which there is at least one point a ≤ i and at least one point b ≥ i + 1."

    I really don't understand the explanation: if a subset s contains xi and xi + 1 and also contains other two points xa been a ≤ i and xb been b ≥ i+1, as points are sorted xa < xi < xi+1 < xb by definition of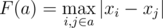 then F(s) = | xb — xa |

    Can someone help me here ?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +7 Vote: I do not like it

      I meant that I'm dividing the whole range a, a + 1, ..., i, i + 1, ...b in edges between neighbours, so the answer is xb - xa = (xa + 1 - xa) + (xa + 2 - xa + 1) + ... + (xi + 1 - xi) + ...(xb - xb - 1). We add each part separately.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        anti-quicksort test ??? seriously ???

        Someone can explain me the point of that test cases ?

        Java use different algorithms just for memory issues not performance.. :(

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          This test was added automatically when someone hacked someone's solution, so you should always be careful using sort on java.

          → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

It seems that Div1B has weak data.

http://codeforces.com/contest/810/submission/27251518[My submission]

I made some mistakes on edge cases that I can't pass the data

8 2
4 7

But I didn't fail the system test.How can I add this data?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    While the event is in progress, you can challenge, and I am pretty sure that successful challenges are added to final tests (even though I could not find this stated anywhere). I don't think this can be done after the competition ended. One option could be creating a mock competition with that problem, but I am not sure how much you can change the data.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in Div2E / Div1C can anybody prove me that the cell(i , j) is equal to (i — 1) xor (j — 1 ) + 1 ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +45 Vote: I do not like it

    The formulation is just an obfuscated form of Nim with two piles.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    I am unable to understand the solution to Div2E / Div1C mentioned above. Can anybody please explain the solution?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I want to join your demand. Can someone, please, give a reference on any valuable information about this type of problems?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +13 Vote: I do not like it

        I will briefly go through probably the most confusing part of the code

        if(a==1&&A[i]==0&&x==1)continue; // and the two lines follow

        This line ensures that the X values considered for dp are LT/EQ to X, another way of putting this line is:

        if(prefix_is_equal && x > X[corresponding_bit]) then skip this state. //If the prefix is smaller then there are no restrictions to the less significant bits

        The state transit below also makes use of the same idea

        dp[i+1][a&(A[i]==x)][b&(B[i]==y)][c&(C[i]==z)] // and the two lines follow

        a&(A[i] == x) implies that the equality flag remains true iff prefix is equal AND the current bit is equal.

        mul(z<<(30-i),dp[i][a][b][c])

        Just to add the values of sum according to the XOR value and the significant of the bit.

                add(res,solve(x2,y2,k));
        sub(res,solve(x2,y-1,k));
        sub(res,solve(x-1,y2,k));
        add(res,solve(x-1,y-1,k));

        Just in case, this is a way of querying 2D plane.

        If you are interested in trying-out similar questions with similar difficulty I'd recommend 747F.

        (These types of DP questions mostly appear as the last Div2 question, it pretty much decides who will be the first of that round as you can see here)

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it +3 Vote: I do not like it

          what does the dp and cnt refer to ? same goes for the dp parameters i failed to understand even tho i read the tutorial many times :( can u please clarify :)

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            dp and sum has the same parameters, namely:

            dp[bitmask position][equality flag for x coord][eq flag for y][eq flag for k]

            bitmask position (i): we are currently evaluating the value of (1<<i), from the most significant to the least, since ...

            eq flags: this represents if the value of {x, y, k} is going to be strictly smaller than our queried upper-bound. If the flag is true, that means we have to be careful of not over-counting stuff because of counting above the upper-bound. If the flag is false, that means the considered value is less than the upper-bound no matter what, so we would consider all transitions.

            The only difference between dp and sum is that dp represents the "ways" of reaching this state, and sum is the weighted value of the dp array.

            → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +37 Vote: I do not like it

        I have linked a proof for why cell (i, j) has value (i - 1)xor(j - 1) + 1 above.

        Let's make a function sum(i, j, k), which gives the sum of all integers less than or equal to k that are in the upper-left i * j fragment of the matrix. We can use that to calculate the answer for any fragment.
        Sum for fragment (x1, y1, x2, y2) is equal to sum(x2, y2, k) - sum(x1 - 1, y2, k) - sum(x2, y1 - 1, k) + sum(x1 - 1, y1 - 1). If you don't know why, research "2D prefix sum."


        How do we compute the answer for that function efficiently?

        Let's come up with an algorithm for computing sum of all x xor y, such that for each x and y such that x ≤ a and y ≤ b and (x xor y) ≤ k. Using that we can easily compute value of sum().
        Let's define dp function bt() which will compute that value for us (we'll add arguments to that function one by one when we need them). For computing the value, let's add binary digits to possible values of x xor y one by one, starting from the most significant bit. Let's add argument i to function bt(), which is the index of the digit we're currently adding.

        Now, for every digit i, there are 4 possibilities: we make the ith bit of x 0 and of y 0 resulting in 0 for (x xor y), or 1 and 0 resulting in 1, or 0 and 1 resulting in 1, or 1 and 1 resulting in 0.
        But how do we know which of these possibilities is valid (i.e. doesn't result in exceeding the limit for x, y, or (x xor y))?

        Suppose we're adding bit 1 at index i in x (while adding bits one by one from most significant to less significant), which initially doesn't exceed a.x would exceed a if and only if we're adding bit 1 at index i, while the ith bit of a is 0, and suffix starting from bit i + 1 of x in binary representation is equal to suffix starting from bit i + 1 of a in binary representation. UPD: by suffix, I mean bits with index i+1 through MAXLOG, which can also be viewed as prefix depending on how you visualize it. I'll call it suffix in this post. By ith bit, I mean bit (1 << i). If it's unclear for you why that's true, here's an example:

        a = 110110000110
x = 11011xxxxxxx (so far)
         ^

        In the above example, we can't add 1, because x would become bigger than a. Note that in this case suffix in a (11011) is equal to suffix in x (11011).

        Another example:

        a = 110110110000
x = 11001xxxxxxx (so far)
         ^

        Here, we can safely add 1 without making x exceed a. That is because suffix in a (11011) doesn't equal suffix in x (11001).

        The same goes for y with b and for (x xor y) with k.
        Thus, we only need to keep track of whether the suffix of x currently equals suffix of a, same for y and k. Thus we add 3 boolean arguments to bt, which becomes bt(i, sufA, sufB, sufK).

        Back to the four possibilities: Pairs (1, 0) and (0, 1) result in 1, thus add to answer (1 << i)*numberOfCellsIn(i - 1, newSufA, newSufB, newSufK)*bt(i - 1, newSufA, newSufB, newSufK). Pairs (0, 0) and (1, 1) result in 0, thus just add tp the answer numberOfCellsIn(i, newSufA, newSufB, newSufK)*bt(i - 1, newSufA, newSufB, newSufK).
        We can compute numberOfCellsIn in a fashion similar to bt().

        You can check my code if it's unclear how to compute newSufs. Also check out my code for how to apply that for computing answer of sum, since I'm too lazy to finish this tutorial and I think I already explained the confusing parts and the rest is easy.
        Note that the dp does $lg(max(a, b,y))*2*2*2
        operations, which is sufficient to solve the problem as there are only 10^4 queries.

        My code is too long because I made functions numberOfCellsIn and bt separately, but I think that only makes it clearer.

        Hope that helps

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I am very grateful to you. It realy helps.

          However,

          a = 000011011011 x = xxxxxxx11011 (so far) ^
          In the above example, we can't add 1, because x would become bigger than >>a.

          Why cant I add 1 at this place and follow it up with 0 afterwards?

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            I'm sorry, that should have been reversed, and it should be called prefix instead of suffix. The most significant bit is on the left instead of the right. I'll fix this

            EDIT: Updated

            → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          last problem of div 2 explained so easily. thanks

          → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

27270104 This is my submission to div1 A and it gets wrong answer can someone help please

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    When you write ans += (arr[i] * ( (b-c) % mod ) ) % mod; modulo operation is performed only for (arr[i] * ( (b-c) % mod ) ) part. So ans is still without modulo

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Here is the modified version of your code. 27270623

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -10 Vote: I do not like it

Hey! I tried the problem 809A but got wrong ans.Please can someone suggest what I did wrong?

Code:

#include<bits/stdc++.h> #define MAXN 100010 #define pb push_back #define mp make_pair #define ll long long #define mod 1000000007 using namespace std; int cmpfunc (const void * a, const void * b) { return ( (int)a — (int)b ); } int main(){ int n,sum=0,power=1; cin>>n; int arr[n]; //set arr:: iterator it,it1; for(int i=0;i<n;i++){ cin>>arr[i]; } sort(arr,arr+n); for(int i=0;i<n-1;i++){ power=1; for(int j=i+1;j<n;j++){ sum+=((arr[j]-arr[i])*(power))%mod; power=(power*2)%mod; } } //it=arr.begin();

cout<<sum%mod<<endl; return 0; // 1 3 4 5 }

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    It looks like an overflow of int

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      but i tried with long long int too but still got wrong ans

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +10 Vote: I do not like it

        You need to do modulo operations each time you do any other operation, cause it can lead to long long overflow otherwise. The real answer for this problem can be as big as 2^300000 is big, so the problem requires to print it modulo 10^9 + 7. Furthermore, your solution is not fast enough for passing all tests.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Didn't get the tutorial for 809A/810C. Can someone help ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Tutorial is very confusing. Here is a much simpler solution:

    http://codeforces.com/contest/809/submission/27245918

    What we are doing here is adding up the sum of each point and all the pairs it can make to the left. For any point i, when we transition to point i + 1, we must do dp[i + 1] = dp[i] * 2 + (2^i — 1) * (difference between i + 1 and i), where dp[i] represent the answer if i is the right endpoint. (^ denotes exponentiation) This is because we can view this as adding difference between i + 1 and i to all the intervals, and the 2^i — 1 is because we want to extend the leftmost interval by diff so we must multiply diff by 2^(i — 1) and the leftmost + 1 interval by diff * 2^(i — 2)... and so on, which adds to 2^i — 1.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I don't quite understand how does the randomly generated prior value of a node helps maintaining the treap while merging in the implementation of Div1D, would someone mind explaining it to me?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If you are using classic binary tree, its depth could be O(n), if the values come in sorted order. When you are randoming priorities and use them while merging, your depth of tree would be O(logn)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ah, I see. That's much more faster to code compared to the spin method.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 809C , can someone help to prove that number in (i,j) is [(i-1)XOR(j-1)]+1 ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The position (i, j) could be regarded as two nim stacks with size of (i-1, j-1), thus the mex value of the set {(a, j) | a < i} + {(i, b) | b < j} is equivalent to the grundy value of the nim state (i-1, j-1), i.e. (i-1) ^ (j-1), plus 1.

    (Search grundy theorem to learn more about the "grundy value")

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Problem Div2C/Div1A, we can also count the number of times xi is added and is subtracted from the result. Consequently, the answer becomes the sum of xi * (2^i - 2^(n-1-i)) for i=0,..,n-1.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    That's right . I solve it this way , too.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone help me debug this code: This code is for "Do you want a Date?" problem. I am getting the wrong answer for test case 6. This will be a great help.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In line 13 1<<var may cause overflow

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It's still not working after considering 1<<var. here is updated one. btw thanks for helping:)

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        i<(pow(2,var))

        Brute-forcing every possible subset is not feasible as you have to consider all 2^(3*10^5) sets, which is going to take a whole bunch of time. You should rethink your strategy a bit. =)

        → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For 809B, the editorial states:

So we always know in which of the halves [l, mid], [mid + 1, r] exists at least one point.

Why is this statement true?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Because if the half doesn't contain a point, it won't give us information, that the closest point is closer than in a half with a point. Why? Because any point in the interval is closer, than any point out.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In the solution of Div1 E.Can you tell me how to prove the formula about the coefficients of C ??? Thanks :)

→ Reply
»
7 years ago, # |
← Rev. 4   Vote: I like it +13 Vote: I do not like it

Hi guys!
I made a video editorial on the problem 'Glad to meet you'. I couldn't solve it during the contest, so I had to get back at it somehow. :-)
We use binary search to find the two points.

Here is the link: Div 415 — Glad to Meet You

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Why did 2B disappear? The problem seems to be removed, and tutorial is not available now.

→ Reply
»
10 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Found the mistake. Sorry for bothering.
Can someone point me the mistake in logic in this solution for 810B? I have wrong answer on testcase 15.

→ Reply