OneClickAC's blog

Algorithm to find frequency of a number in an array within range l to r
By OneClickAC, history, 7 years ago, In English

Hello codeforces community, I was solving this problem (http://codeforces.com/blog/entry/46425) on codeforces and came across an interesting doubt (at least according to me) . I just wanted to know that is there any algorithm for finding frequency of any number in a particular range in an array?

We use Mo`s Algorithm for finding max frequency in a range but is there any other one which is faster for this particular problem of mine (calculating frequency of any number)?

I tried writing an algorithm for it but I believe its too slow to pass in one second. Although I think that my build takes O (n log n) time and queries come out in O (log n) time but I believe it's the uncertainty of hashing that`s making the algorithm slower.

Here is my code — https://pastebin.com/Ypj90749

Note- Please do not tell me the solutions of the codeforces problem. I have already read the editorial and their implementation is pretty simple. I just want to get an answer for my curiosity to be able to learn a new beautiful algorithm (if there is) and help some other learners like me.

  • Vote: I like it
  • +5
  • Vote: I do not like it

Comments Comments (24)
| Write comment?
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Read about merge sort tree it works if there are no updates.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I even thought of this too but I believe it will be even slower than that ( on average ) as it will take o ( log n * log n ) time for answering each query.

    log n for first finding node while traversing and other log n for getting the count.

    That`s why I used unordered_map so that I am atleast free of the other log n .

    → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I thought of a solution using persistent segment tree. It is also O(nlogn) preprocessing and O(logn) to answer queries.

To build the segment tree, we compress the numbers in the array (using rank). Then, we can loop through the range of ranks and add the numbers in increasing rank to the segment tree (each iteration will add elements of one rank only). Now we have a persistent segment tree, with the kth version being able to answer queries specifying what is the number of elements less than or equal to an element of rank k (in a range). Now to obtain our desired answer, we can simply take:

number of elements in the kth version of the tree — number of elements in the (k-1)th version of the tree.

This will give us the number of elements that are exactly equal to that number (i.e. the number of occurences of that rank k element in the entire array). Now you can just limit the query range to find the frequency of the element within a certain range.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for taking time for writing this Lance_HAOH but can you please explain a bit more? Persistent segment tree is a completely new data structure for me and I would love if you can explain your solution in a little more easy way.

    → Reply
»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

You can use a vector to store the positions where a number occurs, for each number!
Then just do Binary Search on the the list of a number to count it's number of occurrences in a range. O(n) Preprocessing and for query. I mean, do upperbound(r) - lowerbound(l) on the list of the positions of the number. If there are updates you can use Policy based Data structures (http://codeforces.com/blog/entry/11080). Then Preprocess and query .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Your solution is good but I believe if I am having a[i] <= 1e9 , then I will have to use map instead of a vector and things will become O(log n * log n) again.

    It will work according to your time complexities only if I have say a[i] <= 1e6.

    Am I correct?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Compress the numbers so it will become O(logn) again.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        What do you mean by compressing?

        I didn`t understand this.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          It means each number turnes into his position in the sorted array built from all unique numbers of the given array. So if non-compressed array is defined by A and compressed by B, then for each i, j holds: if A[i] < A[j] (= or >) then B[i] < B[j] (= or > respectively).

          As far as the maximum element can't be more than n you can use array B more efficiently and without loss of the relations between elements.

          As an example, if A = [38, 100, 100500, 42, 100, 100, 100500], then B = [1, 3, 4, 2, 3, 3, 4].

          → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +7 Vote: I do not like it

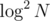      Why ? One 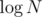is for access to the map and the next 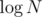is for binary search, not 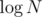binary searches, isn't it?

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    My implementation according to Rezwan.Arefin01:

    Code:
    → Reply
»
7 years ago, # |
  Vote: I like it +34 Vote: I do not like it

If you are allowed to solve it offline (and since you are using Mo's algorithm, I guess you are allowed) then you can do the following:

  1. split each query into freq(r,x)-freq(l-1,x)
  2. iterate over the input and store the counts in an array (or map if the range is big)
  3. if there is a query on your position, add/subtract the count from the array

This should work in O(n + q) if the elements are small enough for array or O(n + q log n) if you need to use map.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for taking time to help me out ania.

    Can you explain point number 2 again or I should say, can you please elaborate it?

    I believe explaining things with a live example will be even better :)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +20 Vote: I do not like it

      Let's say input array is 1 1 2 1 3 and we have queries: X (range=1-2, element=1), Y (range=2-5 element=1) and Z (range=3-5, element=3). Let +X be the upper part and -X the lower part of decomposed query X. In total, we have queries:

      pos=0, queries={-X}
pos=1, queries={-Y}
pos=2, queries={-Z, +X}
pos=3, queries={}
pos=4, queries={}
pos=5, queries={+Y, +Z}

      The iteration goes as follows:

      pos=0, counts=0 0 0, result=0 0 0
process query -X: subtract value counts[1]=0 from result of X
pos=1, counts=0 0 0, result=0 0 0
add element A[1]=1
pos=1, counts=1 0 0, result=0 0 0
process query -Y: subtract value counts[1]=1 from result of Y
pos=2, counts=1 0 0, result=0 -1 0
add element A[2]=1
pos=2, counts=2 0 0, result=0 -1 0
process query -Z: subtract value counts[3]=0 from result of Z
process query +X: add value counts[1]=2 to result of X
pos=3, counts=2 0 0, result=2 -1 0
add element A[3]=2
pos=4, counts=2 1 0, result=2 -1 0
add element A[4]=1
pos=5, counts=3 1 0, result=2 -1 0
add element A[5]=3
pos=5, counts=3 1 1, result=2 -1 0
process query +Y: add value counts[1]=3 to result of Y
pos=5, counts=3 1 1, result=2 2 0
process query +Z: add value counts[3]=1 to result of Z
pos=5, counts=3 1 1, result=2 2 1
      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        I believe there is a reason why your contribution in codeforces community is 100 and I have got that :)

        This is a beauty, such an amazing explaination :)

        Although I will just disturb you for one more thing. You have divided queries into -X and X, what if there are 1e5 queries?

        I mean to ask that how to keep a note of it? I think we can use a map < int , set < int > > for this by storing position as key and query number in value (set of that key).

        We can probably make two maps for this , with one storing positions to add value and other storing positions to subtract.

        I just want to ask if there is any more effective way to do this, because my approach will increase complexity by O(n log n).

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          I would use array of vectors of queries, where query type is up to your preference. It may be just integer +x or -x, it can be a pair (x,+1) or (x,-1) or even a triple like (x,+1,element). Or you can have two separate arrays of vector for + and for -, like you suggested.

          The memory taken is linear because you store only the needed values even though it seems you have nxn array.

          That's quite similar to what you want, but you don't need the log from map because keys are up to n. You also don't need the log from set because you process the whole vector/set at once.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            oh! you are right :)

            Thanks once again ania :) for taking so much time to help a noob like me

            → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +11 Vote: I do not like it

    Here is my implementation, according to reply of ania..

    Code:
    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Thanks for this shahidul_brur

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You are most welcome ! It's my pleasure that my code helps you !

        → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          hey, can you tell me , how can i find frequencies of all the elements in the given range queries [l,r], most optimally?, it would be thankful if you could help me with the code as you did above .Thanks in advance.

          → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Wavelet Tree.

→ Reply