Ahmad_Elsagheer's blog

Actual Complexity of Max Flow Algorithms
By Ahmad_Elsagheer, 7 years ago, In English

Hello everyone.

A few months ago, I read the proof for the complexity of Edmonds-Karp algorithm O(VE2) in "Introduction to Algorithms" and Dinic's algorithm O(V2E) on Maximal. Both proofs are convincing in the sense that they provide a correct upper bound. Also, the output-sensitive complexity O(flow·E) helps in some problems.

However, due to the graph constraints, some problems I encounter make me feel reluctant to:

  1. consider running a max flow algorithm as a subroutine, so I try to come up with another idea.
  2. select the algorithm that will pass the time limit (coding time vs. running time).

Here is an example of such problems: ASC 4 — A. Unique Attack. With the given graph constraints (1 ≤ V ≤ 800, 1 ≤ E ≤ 10000), it seems that max flow algorithms will not pass in 1 second. However, they do! (even Edmonds-Karp).

I was wondering if someone can provide a (quite large generated) test case that is close to the upper bound or maybe share intuitions/approximations/estimates for a tighter bound.

  • Vote: I like it
  • +82
  • Vote: I do not like it

Comments Comments (27)
| Write comment?
»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

Dinic with scaling works in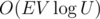 where 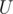is the maxflow. And it's also very easy to write.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I didn't hear before about "Dinic with scaling", so thanks for mentioning it.

    I found a code for it here. If this is the correct/meant implementation for it, then this complexity is not correct.

    Consider the following undirected weighted graph: V = {1 - source, 2, 3, 4 - sink}, E = {(1, 2, 1), (1, 3, 105), (2, 3, 105), (2, 4, 105), (3, 4, 1)}. The algorithm will only push flows of value 1, so it will make at least 105 dfs calls before it terminates. Actually, the algorithm has the output-sensitive complexity, but in a tricky way.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      I'm not sure, can you elaborate why do you think it will push only flow=1?

      There's a path 1->3->2->4 with capacity 105, so first it'll push 2k (so 2k is maximum possible and 2k ≤ 105).

      So for your case it should be around 7 calls to bfs and the same amount to dfs

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Because the algorithm builds a level graph based on distances from source using edges with flow < capacity. It will look like 1 - [2, 3] - 4 (levels are from left to right). So, the edge between nodes 2 and 3 will not be considered because they are at the same level.

        When we reach flow = 1, two pushes are possible 1->2->4 and 1->3->4. After these pushes, flows in edges 1-2 and 3-4 will reach the capacity, and a new level graph 1 - 3 - 2 - 4will be constructed so more flows can be detected using the edge 2-3.

        → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +18 Vote: I do not like it

    Can you explain the complexity?

    Edit: I found it in this article

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +36 Vote: I do not like it

    Hi adamant, I have sended 2 submissions to the SPOJ judge in the FastFlow problem and I get a 1.30s execution with a scaling Dinic and a 0.22s execution with a normal dinics. Is my implementation incorrect or does the scaling only provide a better complexity but a slower runtime?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +10 Vote: I do not like it

      I think this is the complexity question.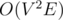 should fail in this problem. Maybe there are no tests on which Dinic itself works with this complexity. Try running both codes on the test provided by ko_osaga below.

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    What about Ford Fulkerson with scaling? Isn’t that O(V * E * log(U))?

    Argument: consider each edge out of source (there are O(V) of them). Each of them will be augmented a maximum of log(U) times with flow and each augmentation takes O(E) time.

    Am I missing something? This seems to be a pretty good complexity for a simple algorithm.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      As I know its complexity is ...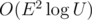

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it +10 Vote: I do not like it

        Yes, I was wrong about every edge being augmented at most log times. Still, O(E2log(V)) is an interesting bound. I wonder how it’s proved or if there’s maximal cases for that.

        → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is a bit slower in practice, isn't it?

    Just to confirm if my implementation was correct (2.5 times slower with scaling for Dinic, but ~ 4 times faster for normal)

    → Reply
»
7 years ago, # |
  Vote: I like it +49 Vote: I do not like it

But still, can someone please provide a "worst-case" for MaxFlow? I have no idea how to go about constructing one of these.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +38 Vote: I do not like it

I was always under impression it's not easy.

There is this paper I found: http://rain.ifmo.ru/~buzdalov/papers/cec15-flows.pdf

There is even some code on github so you can try to generate testcases yourself: https://github.com/mbuzdalov/papers/tree/master/2015-cec-flows

So yeah, this seems like relatively elaborate method. I played with it some time ago, and the cases are not that close to upper bound as you would like. (I didn't try particularly hard though.)

→ Reply
»
7 years ago, # |
  Vote: I like it -64 Vote: I do not like it

Why to learn MaxFlow when you have a president like me!!!

→ Reply
»
6 years ago, # |
  Vote: I like it +18 Vote: I do not like it

We often regard the complexity of max flow as O(be able to pass within the time limit) in China. The only thing we know is that it runs a lot faster than its theoretical complexity. And here is an example: V=10^6,E=4*10^6 and you're asked to get the max flow within 5 seconds. Link to the problem (in Chinese)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +60 Vote: I do not like it

    .. Or maybe tests are just weak? Here are some possible tests that might be missing :

    1

    2

    3

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      What about tests that fail mincost with SPFA instead of Dijkstra? Do you know any?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        I know tests that block SPFA, but nothing about SPFA mincostflow :/

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        I don't think anybody managed to get SPFA accepted on this problem (whereas the intended solution uses Dijkstra). So, if you look at the last 2-3 tests from the attachments you might get an idea about the anti-tests.

        → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    "If you can construct a flow graph from it, 99% of the time max flow related stuff is the solution!" — Pretty much how we handle flow problems

    → Reply
»
6 years ago, # |
  Vote: I like it +31 Vote: I do not like it

Complexity? No idea lol. My approach to flow problems is "write Ford-Fulkerson, hope it passes".

There are different implementations which can produce different runtime speeds, though. For example, you can push a flow in Ford-Fulkerson using BFS or DFS, but DFS (stopped when a flow is found) is usually faster and can give you some bullshit performance (flow++ in const. time) if the tests aren't very strong. When edges have non-unit capacity, you can push the maximum possible flow instead of just +1 at once, which can also help. Finally, randomisation of the DFS can help a lot against those tests where a usual implementation fails.

→ Reply
»
4 years ago, # |
← Rev. 3   Vote: I like it +76 Vote: I do not like it

Today in Round 659 F the tests were week and I uphacked a solution. TBH I was surprised that this counter test was not well known, so I'll share the idea of it so that future problem setters would be aware of this.

It's simple: just span chains of length 1,2,...,sqrt(M) between the source and the sink. In this way, Dinic takes $$$O(M \sqrt{M})$$$ time, which is the worst complexity when all capacities are unit. Besides, we can make even stronger tests by using capacities larger than $$$1$$$. See this implementation for more details.

BTW, when the limit of capacities is a small value $$$V$$$, the complexity of the Dinic is clearly bounded by $$$O(VM \sqrt{VM})$$$, but I don't know if it is possible to achieve that upper bound. Is there anyone who knows about this?

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Dinic takes O(M√M) time, which is the worst complexity when all capacities are constant

    I think it should be "all capacities are unit / 1" instead of all capacities are constant.

    → Reply