Hello Codeforces community,
I would like to invite you to join HackerRank's 101 Hack 50 on June 20, 2017.
There will be five tasks and three hours for you to solve them. The contest will be rated and the top ten contestants will receive HackerRank T-shirts!
The problems are prepared by kevinsogo, nabila_ahmed, zemen, fedimser, and krismaz and tested by shashank21j, allllekssssa, bayleef, wanbo, and kevinsogo. I hope you'll enjoy the problems prepared by the community!
Happy Coding!











And I planned to do round :D
just curious, when world codesprint 12 will be shown in contests??
When they decide to organize it :P
when do u decide to organize it. xD
Well, I believe it most depends of zemen hard tasks :)
I will try to prepare couple of problems for the next month ( I am waiting a lot of time, just need to finish exams), but it is not my decision if they will use on CodeSprint or not — I only can insist :D
How to solve C efficiently . I tried to brute force using string hashing . But I wasn't able to implement it in time . Anyways it would run in O(N3).
I don't want to spoil the solution by seeing the editorial , can someone give some hints.
Think about the solution when you should remove some prefix of the string and insert it as a suffix. When will such operation leave the string unmodified?
Is it anyway related to KMP where we need to find the largest prefix which is also the suffix ?
Yes. Think in terms of rotation of a string. :)
I understood the idea of euler totient function. But there was a approach O(s^2 *log(s)) for finding primtive periods of all substrings.Can you elaborate on it?
I didn't use any of that. I just found the period of each substring (if it exists) and added (r-l+1)/p-1 to the answer, where substring range is [l, r] and p is period.
What was ur idea to find period??
We can basically find the period of any string ( primitive period ) using KMP.
If the length of longest prefix that is also a suffix is 'x' and let 'n' be the length of the string, so the period is n-x if n%(n-x)==0.
So in this question for string of length n, for each starting point l, we make a string from [l,n] and then compute the longest prefix array, which then gives us the period for range [l,r] where l<=r<=n.
Nice technique!!! THanks
Can you share your implementation? I did exactly as you said and i get all the test cases right but i still get last 2 test cases somehow wrong and i tried everything including overflow , double hashes still no luck. @satyaki3794
I did not use hashing at all, but rather KMP.
Code
Thank you!
Can you please elaborate why is calculating the sum of total successful rotations of a substring the answer?
Consider the original string. Suppose you move the substring of length len, which started at index i. Now let the position of that substring in the final string be j. Notice that the part of the original string in the intervals [0, i-1] U [j+len, n-1] is unchanged, so you can completely ignore those.
Consider only the part of the string in the range [i, j+len-1]. This is the part which is modified by the above operation. Observe that the above operation is in fact the rotation of this new string. You have chosen a prefix of length len and made it a suffix. But there is the added condition that the string should not change, i.e. you have to rotate it such that the final string is same as the first one. This is a well-known problem and it is known that to achieve that, the length of the moved string must be a multiple of the smallest period of the string.
I think this is a similar problem.
It also turns out a well optimized O(N3) can pass each case in under .2 seconds.
I got lucky... For D: Frog in Maze, I knew the solution was going to be
gaussian elimination,
but somehow I could use
matrix powers
to simulate DP 2^20 rounds, squeezing within the time limit (1.95s/2s), and pass all the test cases. Also, simulating only ~10^4 rounds already gave me 60.51/65 points.
Hey, can u plz explain ur solution using matrix powers? Also by simulating rounds, u mean to intialize exits by 1, rest by 0, and iterate over all about 10^4 no. of times, right?
(Never mind the spoiler tag then.)
Compute the transition probabilities
X(i.e.,X[p1][p2]: if you're atp1, what's the probability that you'll end up atp2in one step). Nothing enters the obstacles or leaves the mines or exits.Compute
Y = X^N(for some largeN).Y[p1][p2]would be the probability that you'll end up atp2after movingNsteps fromp1, including getting stuck atp2.Sum
Y[start][exit]for allexitcells '%'.This method is only an approximation, but I was surprised it was good enough.
Makes sense that it would work. The matrix equation to solve is (E - T)p = v, where E is the unit matrix and p are probabilities; informally,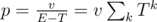 (geometric series), you're simulating just the first x terms. As long as all eigenvalues of T are less than 1 in abs. value, Tk should converge to the zero matrix (about as fast as
(geometric series), you're simulating just the first x terms. As long as all eigenvalues of T are less than 1 in abs. value, Tk should converge to the zero matrix (about as fast as  ).
).