First, I apologize for problems with round and serious problem with Div1A/Div2C. It was very important round for me and, as always, something goes wrong. KAN have already wrote about this.
Anyway, there are problems, so editorial must exists. Due some circumstances, Editorial will be upload in parts. Also, most of tutorials will contain main ideas how to solve task, not ready algorithm.
Tutorial is loading...
code
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)
int c, l, v0, v1, a;
inline bool read() {
if(!(cin >> c >> v0 >> v1 >> a >> l))
return false;
return true;
}
inline void solve() {
int pos = v0;
int t = 1;
int add = v0;
while(pos < c) {
add = min(v1, add + a);
pos += add - l;
t++;
}
cout << t << endl;
}
Tutorial is loading...
code
int n, a;
inline bool read() {
if(!(cin >> n >> a))
return false;
return true;
}
inline void solve() {
int base = n * a / 180;
base = max(1, min(n - 2, base));
int bk = base;
for(int ck = max(1, base - 2); ck <= min(n - 2, base + 2); ck++) {
if(abs(180 * ck - n * a) < abs(180 * bk - n * a))
bk = ck;
}
cout << 2 << " " << 1 << " " << bk + 2 << endl;
}
Tutorial is loading...
code
Tutorial is loading...
code
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)
typedef long long li;
const int N = 1000 * 1000 + 555;
int n, p[N];
inline bool read() {
if(!(cin >> n))
return false;
forn(i, n)
assert(scanf("%d", &p[i]) == 1);
return true;
}
li sum[N], df[N], res[N];
inline void add(int lf, int rg, int k, int b) {
if(lf > rg)
return;
sum[lf] += b;
df[lf] += k;
sum[rg + 1] -= b + k * 1ll * (rg - lf);
df[rg] -= k;
}
inline void calc() {
li curdf = 0;
forn(i, n) {
sum[i] += curdf;
curdf += df[i];
}
li cursm = 0;
forn(i, n) {
cursm += sum[i];
res[i] += cursm;
}
}
inline void solve() {
memset(sum, 0, sizeof sum);
memset(df, 0, sizeof df);
memset(res, 0, sizeof res);
forn(i, n) {
int c1 = i + 1, p1 = 0;
int c2 = n, p2 = p1 + c2 - c1;
int c3 = i, p3 = p2 + c3;
if(p[i] <= c3) {
add(p1, p2, 1, c1 - p[i]);
add(p2 + 1, p2 + p[i], -1, p[i] - 1);
add(p2 + p[i] + 1, p3, 1, 1);
} else {
add(p1, p1 + p[i] - c1, -1, p[i] - c1);
add(p1 + p[i] - c1 + 1, p2, 1, 1);
add(p2 + 1, p3, -1, p[i] - 1);
}
}
calc();
int ans = 0;
forn(i, n)
if(res[ans] > res[i])
ans = i;
cout << res[ans] << " " << ans << endl;
}
Tutorial is loading...
code
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)
#define all(a) (a).begin(), (a).end()
#define sqr(a) ((a) * (a))
#define sz(a) int(a.size())
#define mp make_pair
#define pb push_back
typedef long long li;
typedef pair<int, int> pt;
typedef pair<li, li> ptl;
const int INF = int(1e9);
const li INF64 = li(INF) * INF;
int n[3], m[3], s[3];
inline bool read() {
if(scanf("%d %d %d", &n[0], &n[1], &n[2]) != 3)
return false;
forn(i, 3)
assert(scanf("%d", &m[i]) == 1);
forn(i, 3)
assert(scanf("%d", &s[i]) == 1);
return true;
}
const int N = 2 * 1000 * 1000 + 55;
int ls[N];
inline void precalc() {
memset(ls, -1, sizeof ls);
ls[0] = ls[1] = 1;
fore(i, 2, N) {
if(ls[i] != -1)
continue;
ls[i] = i;
for(li j = i * 1ll * i; j < N; j += i)
if(ls[j] == -1)
ls[j] = i;
}
}
inline vector<pt> fact(int n[3]) {
vector<int> divs;
forn(i, 3) {
int cur = n[i];
while(ls[cur] != cur) {
divs.pb(ls[cur]);
cur /= ls[cur];
}
if(cur > 1)
divs.pb(cur);
}
sort(all(divs));
vector<pt> ans;
int u = 0;
while(u < sz(divs)) {
int v = u;
while(v < sz(divs) && divs[v] == divs[u])
v++;
ans.pb(mp(divs[u], v - u));
u = v;
}
return ans;
}
li ans;
li nn, mm, ss;
vector<pt> fs;
vector<li> bad;
void calcDivs(int pos, li val) {
if(pos >= sz(fs)) {
ans += (val <= nn);
return;
}
li cv = 1;
forn(i, fs[pos].y + 1) {
calcDivs(pos + 1, val * cv);
cv *= fs[pos].x;
}
}
void calcInEx(int pos, li val, int cnt) {
if(pos >= sz(bad)) {
li k = cnt ? -1 : 1;
ans += k * (mm / val);
return;
}
calcInEx(pos + 1, val, cnt);
calcInEx(pos + 1, val * bad[pos], cnt ^ 1);
}
inline void solve() {
ans = 0;
s[0] *= 2;
nn = n[0] * 1ll * n[1] * 1ll * n[2];
mm = m[0] * 1ll * m[1] * 1ll * m[2];
ss = s[0] * 1ll * s[1] * 1ll * s[2];
fs = fact(s);
calcDivs(0, 1);
bad.clear();
vector<pt> fn = fact(n);
forn(i, sz(fn)) {
li cv = fn[i].x;
forn(k, fn[i].y) {
if(ss % cv != 0) {
bad.pb(cv);
break;
}
cv *= fn[i].x;
}
}
calcInEx(0, 1, 0);
printf("%I64d\n", ans);
}
Tutorial is loading...
code
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)
#define all(a) (a).begin(), (a).end()
#define sqr(a) ((a) * (a))
#define sz(a) int(a.size())
#define mp make_pair
#define pb push_back
#define x first
#define y second
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
const int INF = int(1e9);
const li INF64 = li(INF) * INF;
int gcd(int a, int b) {
if(a == 0)
return b;
return gcd(b % a, a);
}
int exgcd(int a, li &x, int b, li &y) {
if(a == 0) {
x = 0, y = 1;
return b;
}
li xx, yy;
int g = exgcd(b % a, xx, a, yy);
x = yy - b / a * xx;
y = xx;
return g;
}
const int N = 200 * 1000 + 555;
int t, n, a[N];
inline bool read() {
if(!(cin >> t >> n))
return false;
forn(i, n)
assert(scanf("%d", &a[i]) == 1);
return true;
}
int pf[N], s;
inline li up(li a, li b) {
return (a + b - 1) / b;
}
inline int findPos(int a, int b, int c) {
li x, y;
int g = exgcd(a, x, b, y);
assert(c % g == 0);
x *= +c / g;
y *= -c / g;
assert(a * 1ll * x - b * 1ll * y == c);
int ag = a / g;
int bg = b / g;
li k = 0;
if(x < 0)
k = up(-x, bg);
if(x >= bg)
k = -up(x - bg, bg);
x += bg * k;
y += ag * k;
assert(0 <= x && x < bg);
k = 0;
if(y < 0)
k = up(-y, ag);
x += bg * k;
y += ag * k;
return x;
}
map< int, set<pt> > cycle;
int ans[N];
inline void solve() {
cycle.clear();
pf[0] = 0;
fore(i, 1, n)
pf[i] = (pf[i - 1] + a[i]) % t;
s = (a[0] + pf[n - 1]) % t;
int g = gcd(s, t);
forn(i, n) {
int st = pf[i] % g;
auto& cc = cycle[st];
int pos = findPos(s, t, pf[i] - st);
if(cc.empty()) {
ans[i] += t / g;
cc.insert(pt(pos, -i));
} else {
auto rg = cc.lower_bound(pt(pos, -i));
if(rg == cc.end()) {
ans[i] += t / g - pos;
rg = cc.begin();
ans[i] += rg->x;
} else
ans[i] += rg->x - pos;
auto lf = cc.lower_bound(pt(pos, -i));
if(lf == cc.begin())
lf = --cc.end();
else
lf--;
ans[ -(lf->y) ] -= ans[i];
cc.insert(pt(pos, -i));
}
}
forn(i, n)
printf("%d ", ans[i]);
puts("");
}
Tutorial is loading...
code
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using D = double;
using uint = unsigned int;
template<typename T>
using pair2 = pair<T, T>;
#ifdef WIN32
#define LLD "%I64d"
#else
#define LLD "%lld"
#endif
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
const int maxn = 305;
int pair3[maxn];
int n;
vector<vector<int>> answer;
void add3(int a, int b, int c)
{
answer.pb({a, b, c});
}
void add4(int a, int b, int c, int d)
{
answer.pb({a, b, c, d});
}
int main()
{
cin >> n;
if (n % 2 == 0)
{
pair3[0] = 3; // 0 1 3
pair3[2] = 1; // 2 3 1
add3(0, 1, 2);
add3(2, 3, 0);
for (int i = 4; i < n; i += 2)
{
add4(0, pair3[0], 1, i);
add3(i, i + 1, 0);
pair3[i] = 1;
pair3[0] = i + 1;
for (int j = 2; j < i; j += 2)
{
add4(j, pair3[j], j + 1, i);
add4(j, i, j + 1, i + 1);
pair3[j] = i + 1;
}
}
for (int i = 0; i < n; i += 2)
{
add3(i, i + 1, pair3[i]);
}
} else
{
pair3[1] = 0; // 1 2 0
add3(0, 1, 2);
for (int i = 3; i < n; i += 2)
{
add3(i, i + 1, 0);
pair3[i] = 0;
for (int j = 1; j < i; j += 2)
{
add4(j, pair3[j], j + 1, i);
add4(j, i, j + 1, i + 1);
pair3[j] = i + 1;
}
}
for (int i = 1; i < n; i += 2)
{
add3(i, i + 1, pair3[i]);
}
}
printf("%d\n", (int)answer.size());
for (auto &t : answer)
{
printf("%d", (int)t.size());
for (auto t2 : t) printf(" %d", t2 + 1);
printf("\n");
}
return 0;
}










Auto comment: topic has been updated by adedalic (previous revision, new revision, compare).
But in both cases we must add 3 arithmetic progression to the segment of array d. Its well known task, which can be done by adding/subtracting values in start and end of segment offline.
Can you please elaborate a bit(or point to some reference) on this well known task?
I a general case when you need to add progressions and answer querys you can use a Lazy Fenwick tree, see this tutorial. Maybe someone knows how yo solve it whitout this structure, I don't.
But in this specific case, you made updates but you have to answer the query just after all modifications are made. So you can made the updates using just 2 arrays
Yes, i will elaborate this with next update
Reference for offline addition(407C)
A"if...else if''solution for div2 C... 28115691
can you please explain your code??
sorry that I failed to prove it when b < a,seems complex...I just think it will be a loop; and when b >= a or the length is short,the answer is sure.there are some mistakes before,now corrected and some comments added
A loop come brute force solution must work I guess. Basically logic I tried out is checking all strings where the repeating character introduced by B is any of the last max(1, a-b) characters. http://codeforces.com/contest/820/submission/28126243
An alternative to handle the even case of 1E is to split the graph into 2 equal disjoint sets A and B. Label the elements a_1 to a_m, b_1 to b_m.
Use induction to construct for A and B separately. What remains is the complete bipartite graph, which can be done using cycles of length 4, all of form a_i — b_(i+j) — a_(i+1) — b_(i+j+1), where i and j run from 1 to m, and indices are taken modulo m.
Can someone please help me understand how Div2 Problem B can be solved in O(1) ?
Here's my submission Well, if you want to find closest angle to a, you just need to find an arc with angle most close to 2*a which its vertices are vertices of polygon. For doing this, you make your ideal arc (with angle 2*a) and find the vertex in polygon which is closest to end of arc.
can anyone explain div2d div1 b more thoroughly . i am not getting it
The solution for Div 2 B is really nice. My solution was to construct the polygon then use dot products and a binary search to find the best end point with two other points fixed. It was really tedious and time consuming to code and had a worse complexity of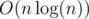 .
.
Can someone elaborate more accurately on Div2 D?
For Div2D / Div1B, one could also keep the amount of elements which holds a[i] >= i to update the difference in O(1) time.
Code with comments : http://codeforces.com/contest/819/submission/28113390
Can you explain your solution a bit more?
To calculate the weighted sum of the (i+1)-th shift from the i-th shift, the elements which holds i >= a[i] (named as gt in the code) contributes +1 to the sum and i < ai contributes -1. That being said, we could solve the problem by simply maintaining the amount of elements which holds true on the above cases.
For non-tail elements, we could easily tell the moment of i < a[i] becomes i >= a[i] is a[i] — i, meaning that we need to account for this moments later.
For the tail element at the moment, we shall recalculate its contribution and placing a new update for it. Note that as a[i] <= n, it is guaranteed that n > a[tail] holds true, so we shall remove one from gt before the update. Same for updating lt for the tail.
Can you please tell me what does upd[i] hold? Actually I don't undersatand what this operation "upd[a[i]+i]++" is doing.
As upd[time] stores the pended update for moment "time", upd[time]++ means that there will be one extra element will switch from contributing -1 to +1. As we are placing a[tail] back to the front, after a[tail] iterations it will hit a[index] == index, therefore we shall place an update on time = a[tail] + current_time = a[tail] + i.
I did it more stupid using segment tree, but calculating indexes carefully is a bit difficult, and each update in log time :P
http://codeforces.com/contest/820/submission/28132944
Awesome solution! Thanks. I understood it and coded myslef but it's giving TLE! I dont understand how a O(n) solution gets TLE?! Code Can you please check it once why its happening
Editted version
I interchanged line 10 & 11 of the original code and it passed all cases, the TLE is most likely caused by initializing the array with size n+2 before n is properly initialized.
For the sake of competitve programming, I would recommend you to use array that has fixed size instead of referring their sizes to variables -- This increases memory usage in practical cases but we only care about the worse case scenario here.
Yea. I figured it out just after submitting the solution in java. In c++ uninitialized variables contain garbage values and no compilation error, however in java you need initialise it. BTW thanks for giving this nice concept to solve the problem
I think my solution of div2D/div1B is a bit easier. We can see that after a cyclic shift our array is always divided into two parts: shifted part and not shifted part. So i just simulated the process. All wee need is two maintain two values for each of two parts: number of such elements that |p[i] — i| will increase after shifting, and number of elements for which this value will decrease. Complexity is O(n). My explanation isn't very good, but code may help you 28121452
I did something similar: http://codeforces.com/contest/820/submission/28127444
Auto comment: topic has been updated by adedalic (previous revision, new revision, compare).
Abstract.
Another (and probably more simple) approach to Div1E.
Here I will suggest a way of constructing a solution for n, given any solution for n - 2. No properties are requested and required to be preserved by such induction.
You still need to solve cases for n = 3 and n = 4 to get the full solution.
The method:
Let's take two nodes, let them be s = n - 1 and t = n for simplicity of numbering.
Consider following paths:
Taking any two of such pathes you form a valid cycle of length 3 or 4. Match listed paths into cycles the following way: first with second, second with third, ..., pre-last with last, and last with first (in other words, match by neighbourhood).
Add such cycles to the answer. Note, that each listed path was used twice by construction above, this way all edges connected to s or t were used twice too.
Continue with n = n - 2 here.
This solution is absolutely brilliant! Thanks for sharing it with us. It's unexpectedly elegant and easy to understand. I've looked for an induction approach but failed to think about it for long because it was hard for me to imagine that I might be able to keep the old construction in its exact form, without some strange alterations.
why editorial link is not there on contest page . I know there is issue with div2-c question but rest of the question are good , i learned and solved div2-d and e(almost done) . good work in editorial and contest adedalic . thumbs up for good work.
There is my solution to 819A - Мистер Б и скучная игра First of all, I guess the color for each segment a is ascending or descending. And for each segment b its color is the minimum or maximum value of the previous paragraph a. We can easily make the interval between l and r no more then 5*(a+b). Thus, you can enumerate the status of each segment and calculate the current answer. Maybe I can't describe it clearly.This is my submission:28097355
The description said: "From multiple variants of t lexicographically minimal is chosen." Why each segment a is descending?
Your solution inspire me.
This is my solution.
For each segment a is increasing then as you said: "for each segment b its color is the minimum or maximum value of the previous paragraph a.", so I separate it to two situation: If a<=b then get the minimum/maximum value in section[lst+1,lst+a] else get it in section[lst+b+1,lst+a].