A. You're given a string...
Iterate over all substrings, starting with the longest ones, and for each one count the number of appearances. The complexity is O(L4) with a small multiplicative constant.
B. Party
It's clear that at least one person (the one with the least number of friends) will have to leave. We claim that at least two persons will leave. Indeed, suppose that only one person left, and he had d friends. Then all other people had more than d friends before he left, and after that they had less than d + 1 friends, i.e. not more than d. So, his leaving influenced the number of friends for every other person, which means that he was friends with everyone: d = N - 1. But he has fewer friends than everyone — a contradiction.
So, the answer is not more than N - 2. We'll prove that it's possible for N - 2 people to stay (of course, if N > 1). The graph of friendship will be the following: take a complete graph on N vertices and delete one edge. Then the degrees of two vertices equal N - 2, and other degrees equal N - 1. After the first two vertices are removed, we have a complete graph on N - 2 vertices, and all degrees equal N - 3, which means that no one else will leave.
C. Oranges and Apples
Sort the boxes in increasing number of oranges. Count the total number of apples in boxes with odd and even numbers. If the boxes with odd numbers contain at least half of all apples, choose them (there are exactly N boxes with odd numbers). If the boxes with even numbers contain at least half of all apples, take them and the last box (which contains the largest number of oranges). It's easy to see that in both cases the conditions of the task are fulfilled.
D. Tetragon
Let ABCD be the quadrangle that we're looking for, and K, L, and M be the middle points of equal sides AB, BC and CD, correspondingly. Let M' be the point symmetric to M with respect to L. Triangles BLM' and CLM are equal by two sides and angle, so BM' = CM = BL = BK, i. e. B is the circumcenter of the triangle KLM'.
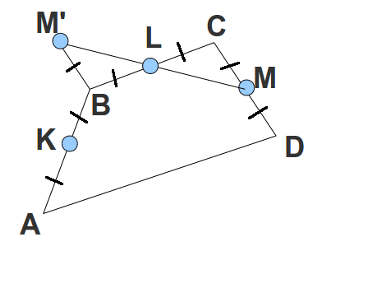
Knowing B, we can reconstruct the whole quadrangle, using the symmetries with respect to the points K, L, and M, and then check whether it satisfies all conditions.
Note that we don't know which of the given points is L, so we need to check all 3 cases.
E. Tree
Lemma. In one of optimal solutions there are no simple paths of length 3.
Proof. We can remove the middle edge from such a path. The connected component will split into two components of sizes a and b, where a ≥ 2, b ≥ 2, and therefore ab ≥ a + b.
We'll root the tree and calculate recursively the numbers hv = the solution of the problem for the subtree with the root v, and fv = the product of hu for all children of v. If v is a leaf, then hv = fv = 1.
We show how to calculate hv, given the solution for all subtrees of v. Consider the connected component of v in an optimal solution. It follows from the lemma that the component has one of the following types:
1. The single vertex v.
2. The vertex v and several children of v.
3. The vertex v, one child of v — w, and several children of w.
In the first case the result of the game is fv.
In the second case it equals Πfi · Πhj · k = Π(fi / hi) · fv · k, where i iterates over children belonging to the connected component, j iterates over the rest children, and k is the size of the component. Since we want to maximize the result, we're interested in children with the largest value of fi / hi. Therefore, the largest possible result in this case equals the maximum value of Πi ≤ s (fi / hi) · fv · (s + 1), where it's supposed that the children are sorted in descending order of fi / hi.
In the third case we can use a similar reasoning for every child w. The best result will be the maximum of the expression fv · (fw / hw) · Πi ≤ s (fi / hi) · (s + 2) as w iterates over children of v, and s iterates from 1 to the number of children of w; note that the children of w have already been sorted in the previous step.
Therefore, the number of operations necessary to calculate fv is proportional to the total number of children and grandchildren of v, which is less than n. The complexity of the algorithm, then, is O(n2) (ignoring operations with long numbers).











Hope that the lack of comments indicates that everything is clear rather than the opposite :)
I would be very grateful if someone could clear this up to me...
> whatever the configuration, there will be no one with exactly N friends, so everyone will have to leave...
When a person leaves, the number of friends for other people changes.
Then how can we get someone to have N friends in the incomplete graph so that person remains in the end? As I understood it, the number of friends for other people will be strictly decreasing as time goes on, so if someone is to have N friends at some point, he must have had at least N friends previously... Either that or I really can't understand the problem...
I think I should be able to understand it best if you could show me an example for a small N...
1--2--3
At the first step no one gets eliminated, since there are no vertices of degree 0.
At the second step the vertices of degree 1 get eliminated and only vertex 2 stays. Now 2 has degree 0.
At the third step no one gets eliminated, since there are no vertices of degree 2.
Thank you for your time and patience.
Can someone explain why the editorial solution to problem C is correct? I've thought about it for a while and still cannot get why selecting all the odd ones, or all the even ones guarantees that it will be correct.
Thanks.
Suppose 0 ≤ x1 ≤ x2 ≤ x2N - 1 are numbers of oranges. Sum the inequalities x1 ≥ 0, x3 ≥ x2, ..., x2N - 1 ≥ x2N - 2. We get x1 + x3 + ... + x2N - 1 ≥ x2 + x4 + ... + x2N - 2. It means that the left part of the inequality (boxes 1,3, …, 2N-1) contains at least half of all oranges.
Similarly, sum the inequalities x2 ≥ x1, x4 ≥ x3, ..., x2N - 2 ≥ x2N - 3, x2N - 1 ≥ 0. We get x2 + x4 + ... x2N - 2 + x2N - 1 ≥ x1 + x3 + ... + x2N - 3. It means that the left part of the inequality (boxes 2,4, …, 2N-2, 2N-1) contains at least half of all oranges.
Now the first subset 1,3, …, 2N-1 contains all odd boxes, and the second one 2,4, …, 2N-2, 2N-1 contains all even boxes. It means that one of them contains at least half of all apples and we may choose it to solve the task.
I am not able to get the logic as why should either of the first subset 1,3,...,2N-1 or second one 2,4,2N-2,2N-1 should contain atleast half of the apples.
Can you please explain ?
If the sum of two numbers is greater than or equal to s, then at least one of them is greater than or equal to .
.
i do not understand the explanation for problem E. please can any one give an easier explanation.
For problem E, an O(n) greedy algorithm is possible (ignoring big numbers). See my code for detail 25487437.
could you explain more ?
Yes. After DFS in a subtree completes, the solution will already make optimal cut in the subtree, and returns a reduced shape that still matter in later decision. Such shape is identified by a integer:
When recursion on all children finished, we keep track of all case numbers for children.
It won't be hard to prove that you can make globally optimal edge-cut decision by just looking at c0, cp, cn, and reduce the subtree into one equivalent case number to return.
what do you mean by [[]] '[' show what ?
each '[' and ']' pair is a node. child nodes are inside parent nodes.
alright ; but why this greedy algorithm works ; i mean why the best possible answer depends on the best answer of its child's ; consider now you are on vertex v and u is child of v ; maybe the best answer of u returns 1-1-fork-k ; but in the best answer of vertex v we have to use u as a leaf ;
That's why u-1-fork-k is one of the reduced cases.
When parent v finishes DFS and reduce its subtree, it can cut (1-fork-k) off, and return a two chain (v-u).
And the already cut part will contribute to answer immediately.
In one of optimal solutions there are no simple paths of length 3 ..
what it mean ?
can anyone please explain me 2nd and 3rd case formula ?
A simple path is a path in a graph which does not have repeating vertices
"Then all other people had more than d friends before he left, and after that they had less than d + 1 friends, i.e. not more than d."
Why couldnt they have had d+3 friends say before and consequently d+2 afterwards?
Because then they will leave at step d+2, and we assume only one person left.
Thanks.
"correspondingly. Let M' be the point symmetric to M with respect to L". Do you still have the picture describing this? Im finding the tutorial hard to follow.
Found it on archive.org: https://web.archive.org/web/20140715212706if_/http://img685.imageshack.us/img685/8097/task.png