Доброго времени суток, недавно я задумался над одной задачей, хочу поделиться с остальными: У вас есть два массива одинаковой длины n, вам нужно посчитать за какое минимальное количество операций обмена двух произвольных элементов первого массива из первого массива можно получить второй. (Элементы первого массива необязательно различны). В поисках эффективного решения Гугл меня ни к чему не привёл. Ясно как решать когда все элементы различны за O(n). Также предположительно есть решение за O(n) и для общего случая, но я не знаю как его проверить. Задача выглядит слишком баянисто. Знает кто как решать такое? Если знаете куда можно сдать, дайте ссылку.
Заранее спасибо!











Почему не [...]? // чет я другую задачу решал
Вот семпл:
2 3 4 5 6 7 1
1 2 3 4 5 6 7
Ответ здесь 6.
Так можно же свести задачу для общего случая к задаче без повторов просто перенумеровав все числа в уникальные (например заменив число на его индекс в отсортированном массиве, сделать это можно за O(n)). UPD. Упустил, что нужно минимальное кол-во
Check out this problem from AtCoder. It's quite possible that you can use a very similar approach (and the answer will be slightly smaller as you can swap arbitrary elements).
If all elements are distinct then solution is with dfs (cycle counting), am I right?
Yes
i know o(nlogn) solution by sorting and using fenwick tree, no matter if elements distinct or not ?
may you explain your o(n) solution for the problem if all elements is different ?
Here check my code for finding minimum swaps to sort (I think it is understandable from code, if you didn't get, write):
he didn't ask for converting the first array to a sorted array.
he asks that he will give you two different arrays, and you want to convert the first one to the second in minimum number of swaps.
like 1 6 3 4 2 to 6 3 1 2 4
ans will be 3
is there o(n) solution for that !
These problems are almost same, just fix array B to {1, 2, 3, .., n}
i think there are not the same,
and by the way, i tested your solution for 3 2 5 1 4 and it output 2, what that means, is it required 2 swaps to sort the element ? how ?
almost same ≠ fully same
Check code below
Btw, my code prints 3 for your array...
Here I just edited code for 2 arrays :)
when arr={1,2} and brr={2,1}, correct answer is 1 but this code gives -1. Can you please elaborate your solution? TooNewbie[user:TooNewbie]
Can we count the inversions of a permutation on N numbers in O(N) complexity?
No
Would you please elaborate that technique to me or share some links? ( I am TooNewbie :) )
Let's build directed graph G = (V, E). V ={a[i] | i = 1 .. n}. E = {(b_i, a_i) | i = 1 .. n}. Now we have to cover this graph with maximal number of edge-disjoint cycles.
Also we can generate arrays for each graph with income degrees equals to outcome degrees.
I think that this problem is NP-hard. But I would happy to know solution if I am not correct.
I couldn't found appropriate article. But for example here http://www.math.ucsd.edu/~jverstra/cycle2.pdf in Introduction is information that problem of packing maximal count of edge-disjoint cycles in graph (both directed and undirected) is NP-hard. I think that our problem is similar.
Yea, I think you can do a reduction from the problem you linked. Let's make a distinction:
Maximal cycle packing: Find a maximal number of simple edge-disjoint cycles in (V, A), not necessarily covering all arcs. Link claims this is NP-Complete*.
Maximal cycle cover: Find a maximal number of simple edge-disjoint cycles in (V, A), such that each edge is covered by a cycle. We want to prove this is NP-Complete.
Lemma 1: a graph has a cycle cover if and only if indeg(v) = outdeg(v) for all v (trivial)
Suppose we can solve the maximal cycle cover problem efficiently. Given a digraph (V, A) to solve the maximal cycle packing problem on, we add one extra vertex u', and for every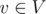 , if indeg(v) > outdeg(v) we add indeg(v) - outdeg(v) arcs** from v to u', and vice versa if the inequality reverses. This gives us a new digraph (V', A'). Note: clearly indeg(v) = outdeg(v) for all v (including u') in the end, so (V', A') has a cycle cover.
, if indeg(v) > outdeg(v) we add indeg(v) - outdeg(v) arcs** from v to u', and vice versa if the inequality reverses. This gives us a new digraph (V', A'). Note: clearly indeg(v) = outdeg(v) for all v (including u') in the end, so (V', A') has a cycle cover.
Now suppose that you have an optimal cycle packing on (V, A) with k simple cycles, then you can extend this to a solution for the cycle cover problem on (V', A') with k + indeg(u'): first we remove all these cycles from (V', A') (recall that (V, A) is contained in (V', A')). This doesn't change that fact that indeg(v) = outdeg(v) for all v, so the resultant graph still has a cycle cover. In addition, there are no cycles that don't pass through u' (otherwise, we could add this cycle to our packing for (V, A)). Thus, after removing the cycle packing on (V, A) from (V', A'), we can decompose the remains of the graph into exactly indeg(u') simple cycles (quickly, using e.g. Hierholzers algorithm). So we proved:
Thm 1: A optimal packing of k cycles in (V, A) gives rise to a cover of k + indeg(u') cycles in (V', A').
Conversely, suppose we have an optimal cover of k' simple cycles over (V', A'), then there must be exactly indeg(u') simple cycles going through u' (_exactly_ indeg(u') since this is a cover). Remove these cycles, and you end up with a cycle packing with k' - indeg(u') simple cycles in (V, A). Thus:
Thm 2: An optimal cover of k' cycles in (V', A') gives rise to a packing of k' - indeg(u') cycles in (V, A).
This clearly implies that the optimal solution to the cycle packing problem on (V, A) differs from the cycle cover problem on (V', A') by indeg(u') (a constant that depends only on (V, A)), and that we can efficiently reconstruct such a packing, given an optimal cover. Thus, the cycle cover problem is also NP-Complete.
*: The linked paper claims it is NP-Complete but doesn't provide a proof. I can't find any either (other than two more papers making the claim without a proof or citation).
**: Not sure if we're allowing multi-edges, but clearly you can replace k copies of (u, v) with (u, wi) and (wi, v) for k new vertices wi, without really affecting the problem.