A. You should iterate over all dices from up to down and restore answer. You can easily find number of the bottom side of the 1st dice. Using known sides of the 2nd dice you can find pair of numbets on top and bottom side of the 2nd dice. If one of them equal to number on bottom of the 1st dice, you can restore all numbers on the 2n dice. Then using this idea you can try restore numbers on the 3rd dice and so on. If you restored all numbers, you should write YES. If for some dice you cannot uniquely determine order of numbers on the top and botton sides, there will be at least 2 placing of numbers. In this case you shoyld write NO.
Author is Ripatti .
B. Firstly you should generate all k-bonacci numbers less than n. For k ≤ 32 you can do it straightforward, for bigger k you can see that all k-bonacci numbers less 109 are powers of two only (and 0). So you will have no more then 100 numbers.
Then you should use greedy algo. You should substract from n maximal possible k-bonacci numbers. You should repeat this operation while n is not decomposed. And in the end you will have answer.
Why all numbers will be different? One of possible proves:
F(k, n) = F(k, n - 1) + F(k, n - 2) + ... + F(k, n - k)
F(k, n - 1) = F(k, n - 2) + F(k, n - 3) + ... + F(k, n - k - 1)
You can substract the 2nd equation from the 1st one and you will recieve F(k, n) + F(k, n - k - 1) = 2F(k, n - 1), that equal to 2F(k, n - 1) ≥ F(k, n). This unequation also holds for n ≤ k.
Suppose than greedy also constricted 2 equal numbers F(k, x) in decomposition. But then in virtue of unequation we should take number F(k, x + 1) insead these 2 numbers. Сontradiction.
But you didn't need prove than greedy algo works, you might believe that it works:)
Authors are Gerald , Ripatti .
C. Firstly you should calculate number of white and black pixels in every column. After that you should calculate number of white and black pixels for every prefix in sequence of columns. Now you can calculate number of black or white pixels in every vertical line of any width in O(1).
Now you should use dynamic programming. Let's dp[i][j] will store numbers of repainted pixels in prefix from the 1st column to the j-th and color of the last column will be white for i = 0 and black for i = 1.
Than you can recalculate dp using forlulas: dp[0][0] = dp[1][0] = 0 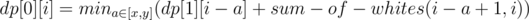
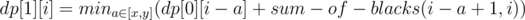
Answer will be min(dp[0][m], dp[1][m]).
This solution works in O(nm + m * (y - x)).
Author is Ripatti .
D. There is just BFS. State is head place and mask that store place of tail: using 2 bits you can code position of every segment in relation to previous segment. Mask will contain no more than 16 bits, and number of all states will be no more than 48 × 15 × 15 (also you can try understand that number of states no more than 38 × 15 × 15).
Then you should just carefully implement it.
Author is Ripatti .
E. You have z = [x / 2] + y + xy. That is equivalent to
z = [2k / 2] + y + 2ky, where x = 2k, k > 0
or
z = [(2k + 1) / 2] + y + (2k + 1)y, where x = 2k + 1, k ≥ 0.
z = k + y + 2ky, k > 0
or
z = k + y + (2k + 1)y, k ≥ 0.
Still more steps:
2z + 1 = 2k + 2y + 4ky + 1, k > 0
or
z + 1 = k + 2y + 2ky + 1, k ≥ 0.
2z + 1 = (2k + 1)(2y + 1), k > 0
or
z + 1 = (2y + 1)(k + 1), k ≥ 0.
From the 2nd equation you can see than z should be 2t - 1 because otherwise z + 1 will have odd divisor and we can build solution. From the 1st equation you can see that 2t + 1 - 1 should be prime, otherwise we also can build solution. If z = 2t - 1 and 2t + 1 - 1 is prime, obliviously there are no solutions.
Prime numbers like 2a - 1 are Mersenne primes. Only about 46 such numbers are found now. Powers of 2 for the firts 40 numbers you can find for example here.
Author is Ripatti .











about D,i have other solution,easy to implement. just do it as normal BFS first , and we can think now the snake adjust it's head. After adjustments , snake can go to the @ directly ans at this time we think it's tails as wall. In fact i use force to find 100,000 states first , and from every states i use another bfs to let snake try to eat food.
In problem D, I understood that using 2 bits we can encode that how can we get from a previous position to new position. 2 bits are used to represent whether the head moves left, right, forward. Next thing we need to encode in state is representation of present position of snake which I guess is done by mask. I couldn't understand how can we represent the mask using 16 bits.
We can use mask to describe the position of i-th segment of snake relative to the i-1-th segment(for example,0 for left, 1 for down, 2 for right and 3 for up.) There are at most 9 segments, we need to encode 8 of them. That's why we need 16 bits. After making such mask, you can go through all 4 directions and find, which mask we'll have after moving to this direction.
My english is very bad and i can't understand what the author means when he says in the solution of the problem C :"After that you should calculate number of white and black pixels for every prefix in sequence of columns." What does he mean for prefix? =(
Prefix means number of first elements, i.e one of prefixes for string "abcahkjdf" is "abc"
You can solve problem B using binary search.
There are 47 mersenne primes dicovered not only 46!
http://mathworld.wolfram.com/news/2009-06-07/mersenne-47/
For problem B, is there any proof why greedy works?
Also, do you understand, why there should be only 100 numbers at max?
Can anybody guide me, I am not able to pass test case #14 of DIV2 C. Here is my solution...
My submission
Can anyone explain me how we are ensuring that no column is less then x size in problem statement C ? I got AC however it was calculating for vertical lines being less than x but I am unable to understand how it is ensured.