AtCoder Grand Contest 019 will be held on Saturday (time). The writer is tourist.
The point values will be 300 — 500 — 900 — 1000 — 1700 (1200) — 2000 (1500). Note that the contest duration is unusual (150 minutes).
Let's discuss problems after the contest.











It is very pleasing as well as fearing to see you as a contest writer tourist.
Yesterday I had to cancel my weekend plans and got upset by that. Now I'm not that upset anymore.
tourist round? Oh Yeah!
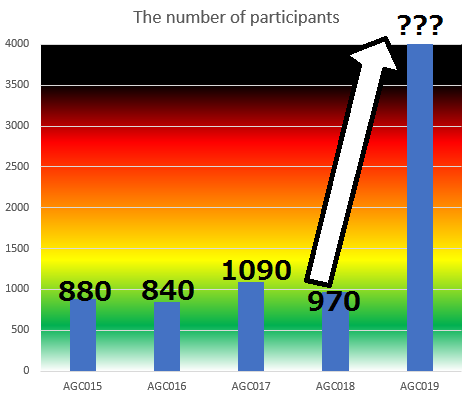
~ 1432 users
Special mention when tourist is the problem setter:
I hope to get well in this contest, this wink has to mean something..
Looks like the whole world is waiting for this contest -> I hope that servers will handle such a huge number of participants.
Did anyone else get WA in last 4 tests in C?
Case like that:
0 0 3 1
2
1 0
2 1
I think i considered that, so what's correct output?
402.831853071795862
And how can we achieve this?
Sorry, my mistake 407.123889803846897
I have the same, so i've missed something else
The last 4 cases were similar but with x & y swapped. Try this
0 0 1 3
2
0 1
1 2
Any hints for C?
x1 = x2 and y1 = y2 are not the only special cases.
how to solve B ? :)
Consider all contiguous regions.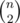 of them. Now a [l... r] is superfluous if a[l] = a[r] as [l + 1... r - 1] is already checked. Subtract these from that.
of them. Now a [l... r] is superfluous if a[l] = a[r] as [l + 1... r - 1] is already checked. Subtract these from that.
okay thanks :)
I get it :D
Good day to you,
well a good hint is, that as long as "borders" of reversed substring are equal, then the string after reverse will be same as if it was reversed without borders.
Also note that if this wouldn't happen, then |s|*(|s|+1)/2 (+1) possible solutions could apprear.
Hope it helped a little bit.
Good Luck & Have Nice Day ^_^
oh okay :P
I was so stupid :)
thank you :)))
Solution for B is so simple but too difficult to come up with. ;(
How did you come up with it?
It's obvious that if substring is palindrome reversing it won't change anything. And I noticed if s[l] = s[r], then reversing it will be same as reversing [l + 1, r — 1], so you need to substract such pairs.
The hard way:
My first three steps were the same as yours :)
Then atleast someone suffered like me. My steps:
Look at points : 500 => Easy.
Look at problem : WTF, how to solve?
Think for some time, figure out swapping palindromes is invalid.
Look at "abracadabra" : HTF is answer 44? How can 11 be bad?
Look at standings : People solving trivially in 8 — 10 minutes.
Start discarding Manacher. What is trivial and seems correct?
No idea, write brute force Python code, print all invalids.
Endpoints equal means invalid, scold yourself for being dumb.
Believe in God, and that your observation is the sufficient condition.
Code.
and these are my steps :D :
1.read problem !
2.WTF :D
3.after about 10 min think , I guess that it need some algorithm that I don't know !
4.close contest page and go to my bed and sleep :))))
My way:
Oh, that 54 is familiar :D I was afraid I'm the only one here, facing side effects of droptable coaching me for ICPC :)
I really loved this problem — it made me feel stupid, then I had to guess solution from standings (there are not so many simple things you can do with string in 2 minutes), and then after figuring out why is it correct (only after the contest) I was amazed how simple&obvious it is.
It is also funny how it uses some simple but not worn-out idea, but everybody goes into palindromes because they have been hyped a bit over last years :)
I also stuck with this problem , ended up by doing it bruteforce(print out all of the same strings with different left and right) and finally got it xD
I have an easy solution to E in O(n2) with a sufficiently small constant, without using NTT, unlike 998244353 suggested. (
p.s. I didn't bothered to check other solutions.It appears that first solvers have the same solution.)We first observe that any valid swap is either:
Let x be the number of (0, 1) and y be the number of (1, 1). Clearly the number of type 1 swaps is x, and the number of type 2 or 3 swaps is y. As type 3 swaps do not interfere with other types, we assume there are y - i of them, multiply the answer by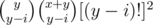 , and forget their existence.
, and forget their existence.
Now we're left with x of (0, 1), i of (1, 1), and only type 1 or 2 swaps. Let g(x, i) be the number of possible swap sequences. Clearly,
Let g(x, i) = (x!)2(i!)f(x, i). Then clearly,
And for the final answer, we must sum over 0 ≤ i ≤ y, i.e.
I think that tourist knew about this solution and made constraints lower for this to pass. If the only intended complexity was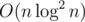 then why n is not up to 105?
then why n is not up to 105?
Better ask tourist directly for the reason.
Anyway, I'd still post the comment as long as most of the world didn't know about this solution.
Thank you for describing your solution! It's quite different from the editorial, so it's definitely worth explaining.
Indeed, we had only intended, but shortly before the round discovered that it's nearly impossible to separate it from O(n2). Thus, we decreased the constraints to make it obvious that O(n2) works.
intended, but shortly before the round discovered that it's nearly impossible to separate it from O(n2). Thus, we decreased the constraints to make it obvious that O(n2) works.
It took a lot of work, but I was able to squeeze in a solution of F in .
.
Let's first consider the case where N = M, and compute A[x] — the sum of the results over all possible Yes/No sequences. Clearly, A[0] = 0.
We model the Yes/No sequence as lattice path from (N, N) to (0, 0). What happens at point (x, x) for x > 0? There will surely be a point where the path crosses the main diagonal again for the first time, that is, we reach state (y, y) for some 0 ≤ y < x.
How many ways to do this are there, and how good they score? Let's assume that the we guess incorrectly at (x, x) and we move to a state (x - 1, x). Then, our path continues to (y, y + 1) and then continues to (y, y). It is the first time we reach the main diagonal, thus the path never crosses the "+1" diagonal. There are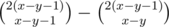 such paths. Since it is optimal to always guess the answer which has the most occurrences left, it is easy to see that this path scores exactly y points, plus whatever we expect to get from the path between (y, y) and (0, 0).
such paths. Since it is optimal to always guess the answer which has the most occurrences left, it is easy to see that this path scores exactly y points, plus whatever we expect to get from the path between (y, y) and (0, 0).
Similarly, if we guess correctly at (x, x), we have the same amount of paths to (y, y), but we score one more point (the one at (x, x)).
This combined yields the following recurrence: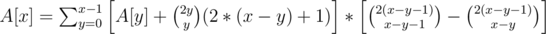
The second summand in the large sum times the right term can be computed first by a simple convolution. The term with A[y] can be then computed using linear convolution (of form ) in
) in 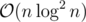 time.
time.
This yields 1500 points and fits quite comfortably into TL. To extend this to a full point solution, we need an extra linear step: for every point (x, x) we calculate how many paths there are for which this is the first point on the main diagonal from the path from (N, M) (again by using the above formula for lattice paths above the diagonal) and for each of them add M - x points to A[x].
The TL is very tight in this case, so one needs to have solid NTT implementation, and when doing the linear convolution using Divide & Conquer algorithm (described here), one needs to cut-off the recursion at around 26.
My quite convoluted (pun intended) solution: link
EDIT: The editorial seems not to be present anymore, so I wasn't able to verify how much my solution matches it :)
Maybe his mind is weak
could someone explain the "simple binary coefficient" for me :D
As expected, problems were very interesting. Words cannot explain the pleasure of a post-AC orgasm from this contest's problems.