It is needed just to implement actions described in statement. You had to read data and to calculate number of members of team, which were sure about the solution, for every task. If this number is greater than one, the answer must be increased by one.
231B - Magic, Wizardry and Wonders
Let's see, what will be the last number of array after i iterations. After the first iteration it will be an - 1–an (and total number of elements will be decreased by one). After the second iteration the last number will be an - 2–an - 1 + an. It is not hard to see, that after n - 1 iterations remain a1–a2 + a3–a4 + ... + ( - 1)n + 1·an. In a such way, our task is to put numbers from 1 to l in array so, that sum of numbers in odd positions minus sum of numbers in even positions will equal to given d. This means sum of numbers in odd positions must be equal 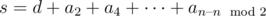 . But the minimal sum can be
. But the minimal sum can be 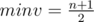 , and the maximal —
, and the maximal — 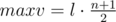 .
.
Because of this we should choose a2·k so, that s fits the boundaries. Constrains allow to do it in a such manner. Firstly, put ones on the even positions. If s > maxv after that, the answer is - 1. Otherwise, let's increase each a2·k by one until s = minv. If we put l in all even positions and s < minv, than answer is - 1 too. After we put numbers on even positions, let's write 1 in all odd positions, and while sum of this elements is less than s increase each one by fitting value.
One of the main observations, needed to solve this problem, is that the second number in answer always coincides with someone aj. Let's see why it is true. Suppose, the second number of the answer is aj + d for someone j and aj + d ≠ ai for all i. This means, we increased some numbers, which is less than aj, so that they became equal to aj, and then all this numbers and some numbers, which is equal to aj, we increased to aj + d. But if we didn't increase all this numbers to aj + d and remain they equal to aj, we'd perform less operations and the answer would be better.
Due to this fact we can solve problem in a such manner. Sort array in non-decreasing order. Iterate over ai and calculate, what is the maximal number of ai we can obtain. For maximizing first number of answer, we must increase some lesser numbers to ai and perform not greater than k operations. It is obvious that firstly we should increase such aj that ai–aj is minimal. So, if we can solve problem in O(n2), we would iterate j from i to 0 and increase aj to ai, while we could. But the solution must be faster, and we will use binary search. We will brute the number of numbers, which we must do equal to ai. Suppose we fix cnt this value. Now we have to check if we can do cnt numbers equal to ai by not greater than k operations. For doing this, let’s calculate 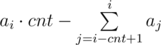 . If this value not greater than k, we can do it. For calculating sum quickly, we can save prefix sums and than si - cnt + 1, i = si–si–cnt. Finally we solved this problem in O(n·logn).
. If this value not greater than k, we can do it. For calculating sum quickly, we can save prefix sums and than si - cnt + 1, i = si–si–cnt. Finally we solved this problem in O(n·logn).
The main subtask of this problem is to check whether we can observe the center of face of parallelepiped from point p = (x, y, z). Let’s see the case, when the face belongs to plane z = z1. For performing all calculations in integer numbers, multiply all coordinates x, y, z, x1, y1, z1 by 2. Take the point 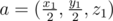 and normal to plane, containing the fixed face, which is directed out of interior of parallelepiped, that is
and normal to plane, containing the fixed face, which is directed out of interior of parallelepiped, that is 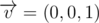 . Also take vector
. Also take vector 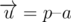 . If undirected angle between this vectors is less than 90 degrees, we can observe a from p. For checking this we can use scalar product. If scalar product of
. If undirected angle between this vectors is less than 90 degrees, we can observe a from p. For checking this we can use scalar product. If scalar product of 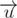 and
and 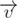 is strictly greater than zero, than that angle is fitting.
is strictly greater than zero, than that angle is fitting.
In this problem you should find the number of simple paths between some pair of vertices in vertex cactus. If you learn the structure of these graphs, it is not hard to see, that if we’ll squeeze each cycle in one vertex, we get a tree. So let’s squeeze all cycles in source graph and get this tree. Also every vertex of this tree we’ll mark, if it is squeezed cycle (let’s call this vertices 1-vertices) or single vertex in source graph (this vertices we’ll call 0-vertices).
Then, we’ll do the following to find the number of paths between vertices a and b in source graph. Suppose c is a vertex, corresponding to a in obtained tree (it can be a single vertex or a vertex, corresponding to a squeezed cycle with a), and d is a vertex, corresponding to b. Let’s denote deg is the number of 1-vertices in path from c to d in tree. Than it is easy to understand, that the answer for query is 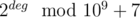 , because every cycle (1-vertex) increase the number of possible ways twice (you can go from one vertex to other by two ways in cycle).
, because every cycle (1-vertex) increase the number of possible ways twice (you can go from one vertex to other by two ways in cycle).
It means that we need to count the number of 1-vertex on the path from one vertex to other in tree quickly to answer a query. We can do it in a following way. Hang our tree for one vertex, which we’ll call a root. Denote for every vertex cntv is the number of 1-vertex on the way to the root (including root and vertex itself). Suppose we want to find the number of 1-vertex on the path from a to b. Denote c is the least common ancestor of vertices a and b. Than number of 1-vertex on the way from a to b is equal to cnta + cntb–2·cntc, if c is 0-vertex and cnta + cntb–2·cntc + 1, if c is 1-vertex. The least common ancestor can be found by standard method — binary method recovery. Finally we have O(m + k·logn) solution.











I solved Problem B by dfs :
Lets maintain two arrays ,d[] the array of differences and a[] the array of numbers . Initially d[0]=d . Now we know that a[0] lies in the range of [1...L] and a[0]-d[1]=d[0] => d[1]=a[0]-d[0].So we need to iterate over all possible values of a[0] i.e [1..L] and check if it is going good .Similarly we check for d[1] and keep digging deeper until we reach the base case ( index=n-1) . My code implementing the above idea code ..As you see the code exceeded time on pretest 10 (call it lucky or unlucky).
So other thing to observe is what is the maximum ans minimum values that the difference array can take. With this we can prune the tree into avoid going to some branches which are unncessary . Lets take the trivial values of max and min for the last location . i.e . d[n-1] as max[n-1]=L ans min[n-1]=1. Now max[n-2]=L-min[n-1] and min[n-2]=1-max[n-1] .So like this , we make up these two arrays . And everytime we are calling the dfs function we check if the d value is in the range of max and min .Code
It will be great if you can post the implementation code for these solutions as well.
If you really need them, you could see other participants' solutions in the standing page.
this is the solution of A.team
include
include
using namespace std; int main() { int n,i,j,c; vector v; cin>>n; int arr[n][3]; for(i = 0;i<n;i++){ for(j = 0;j<3;j++){ cin>>arr[i][j]; } } for(i = 0;i<n;i++){ c = 0; for(j = 0;j<3;j++){ if(arr[i][j] == 1){ c = c+1; } } if(c >=2){ v.push_back(1); } } int ans = 0; for(i = 0;i<v.size();i++){ ans = v[i] + ans; } cout<<ans; return 0; }
Why there is no English tutorial, I can't understand Russian...
http://codeforces.com/blog/entry/5486
Change the url from http://codeforces.com/blog/entry/5486 to http://codeforces.com/blog/entry/5486
Or simply press the British flag on the top right corner of the page
Warning — I am a complete newb at online coding competitions, so if dealing with people like me causes you lots of frustration, please just ignore my comment and pass on!
I competed in this competition (only submitted on 231A Team) I was wondering if someone might hop into a 'talk' me and help me understand why my solution was incorrect (my code is so ugly I dont want to post it here)? I had it working fine my version of Visual Studio, but when I submitted it didn't pass the first test...think it's probably something to do with how I read the stdin...
Any help gratefully received — thanks. ahab
There are spaces between the numbers in the input data. Your method of inputting data is weird. Why use
strings andstringstreams if you can read numbers directly fromcin?Thanks for the reply — you're right. It was weird to use
string(The perils of being newb coder!) and I just realised my error this morning with the spaces between the letters when I started stepping through someone else's succussful submission. Thank you for taking the time to look.Out of interest, when you are coding and debugging your potential submissions, how do you replicate the standard input? Do you set up the examples given in the problem in a file and point
cinto that, or do you type them in by hand as required by your code as you execute a trial run?One popular way to do it is to store test input in a file and then insert
#ifndef ONLINE_JUDGE freopen("input.txt", "r", stdin); #endifat the beginning of
main().Then you would use
cinas usual. TheONLINE_JUDGEmacro is defined on Codeforces, so this code will redirectcinif you compile it on your computer and will still read from standard input if compiled on Codeforces. You can also do the same for output withfreopen("output.txt", "w", stdout);.Then there is a problem of inputting multiple test cases. Many people deal with it like this: they store all tests in one file, and in the main program write
while (cin >> first_variable_of_input) { // Read remaining data for this test case // Process data and print the answer }While there is something yet to be read from file, this loop will begin anew, allowing to process many tests at once. But be careful to re-initialize all global variables each time. I won't say this is the best solution, but it is simple and quick enough to write.
Could somebody help me with the sample for problem E: points 3-5, isn't the number of simple paths equal to 3? 3-2-1-4-3-5, 3-4-1-2-3-5, 3-5? what am i missing?
For E — Cactus, can someone explain the algorithm needed to "squeeze" the cycles?
Could anyone explain this part in the editorial for 231C please?
" Suppose we fix cnt this value. Now we have to check if we can do cnt numbers equal to ai by not greater than k operations. For doing this, let’s calculate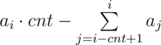 . If this value not greater than k, we can do it. For calculating sum quickly, we can save prefix sums and than si - cnt + 1, i = si–si–cnt."
. If this value not greater than k, we can do it. For calculating sum quickly, we can save prefix sums and than si - cnt + 1, i = si–si–cnt."
P231C is possible in O(n) using two pointers. First Input n,k,array (a). Sort array a.
You need mocc and mnum.
I didn't understand the part:
please explain, thank you.
we are restoring back the total difference, tdiff.
While your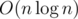 ..., the time complexity still same as the official solution:(
..., the time complexity still same as the official solution:(
sortis inSolution to div2 C using 2 pointers . Works in O(n) apart from sorting
code
Can you explain how you used two pointers in this?I solved using the author's solution
sort() == O(nlogn)
apart from sorting
A much easier to solution D is to simply check for each dimension whether the observer's position for that dimension is less than 0, more than x1/y1/z1, or in between.
For example, if observer's x is less than 0, the a5 side will be visible no matter the observer's y and z, if the observer's x is more than x1 (where the cube ends) then the a6 side will be visible no matter the observer's y and z. Do the same for the other 2 dimensions and you get the sum. No angle calculations necessary.
Program: https://codeforces.com/problemset/submission/231/53533694
Pls, tell me whether my logic for E is correct or not.
Since it is a cactus, we can detect all cycles within o(n), I will mark different cycles with different colors(such that the nodes within the same cycle have the same colors), such coloring is possible cuz one vertex is a part of at most one cycle.
To respond to the query, I would check 3 cases. I) Suppose their color is the same, then there are 2 possibilities to reach from end x_i to y_i.
ii) Suppose their color is different color then there would be always 4 possible ways.
iii) if some node is not colored, it means it is not part of any cycle, thus there would be only one path to reach that node (if both the nodes are not colored), 2(if one node is colored and the other is not(