As the title says, there are these two types of queries. number of values (n) <= 100000 and number of queries <= 200000, the solution that came to my mind is using a segment tree, where each node of the segment tree is an AVL tree that stores the elements of the segment tree node interval in ascending order, and each node of any AVL tree will store the sum of elements of the subtree rooted at this node.
So if I need to update an element (write a new value to it), I go to the segment tree nodes whose intervals contain the position of the element (log(n) nodes) and update the AVL tree of each of these nodes (each update is log(n)), so in total (log(n))^2.
And if I want sum of numbers less than x in interval l to r, I do a query operation so that when the segment tree node is totally inside l to r, I use the AVL tree of this node to get sum of elements less than x in log(n) complexity, and the higher level segment tree nodes will return the summation of these lower level segment tree nodes' sums (so in total (log(n))^2).
If number of queries/updates is Q, their complexity becomes Q*(log(n))^2. am I walking in the right path or is there something wrong in this approach ?










Compressed segment tree, counting points (ai, i) in the rectangle [0, x] × [l, r]. Complexity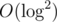 per update/query. It was used in several problems, mainly IOI'13 Game.
per update/query. It was used in several problems, mainly IOI'13 Game.
Would you please provide a good link for this?
It's an IOI problem ffs, can't you look it up yourself? Here
I mean a link for compressed segment tree.
Same link. Last problem, Game. It uses a compressed segment tree. The code should be there too.
If the problem is already available in an OJ, could you please share the link?
You can try implementing the solution to 848C - Goodbye Souvenir after reading the editorial on how it can be reduced to this problem.