phoaiphuthinh's blog

Maximum Sum Subsequence Non-Adjacent
By phoaiphuthinh, history, 6 years ago, In English

I've a big problem: Given N number a[1],a[2],..,a[N] and M queries. (N,M <= 10^5)

Each query, change a[v] to x, and find the maximum sum subsequence such that no two elements are adjacent.

Example: a = {1,1,1,1,1,1}

  • First query, change a[5] to 3, thus a = {1,1,1,1,3,1} -> the answer is 5 (choose a[1],a[3],a[5])

  • Second query, change a[2] to 4, thus a = {1,4,1,1,3,1} -> the answer is 7 (choose a[2],a[5])

  • And so on..

I think use DP to solve this problem, but the complexity is O(N*M) can't run with N,M <= 10^5.

Could you help me? Thanks all.

UPD: I've solved this problem, thanks for all.

  • Vote: I like it
  • +13
  • Vote: I do not like it

Comments Comments (6)
| Write comment?
»
6 years ago, # |
← Rev. 3   Vote: I like it +24 Vote: I do not like it

To handle updates we will use a segment tree. Each node [l;r] will contain the following:

  • answer if ar is the last chosen element and al is the first chosen element
  • answer if ar is the last chosen element and al + 1 is the first chosen element
  • answer if ar - 1 is the last chosen element and al is the first chosen element
  • answer if ar - 1 is the last chosen element and al + 1 is the first chosen element

For shorter notation I will use f(i, j) as the answer if the first included element is ai and the last is aj. Then in other words in a node we will keep f(l, r), f(l + 1, r), f(l, r - 1) and f(l + 1, r - 1).

Now the merging of two nodes can be done in constant time. Lets have two adjacent nodes (L1, R1) and (L2, R2). The conditions L1 ≤ R1 < L2 ≤ R2 and R1 + 1 = L1 hold. Then the merged node will have:

f(A, B) = max(f(A, R1 - 1) + f(L2 + 1, B), f(A, R1) + f(L2 + 1, B), f(A, R1 - 1) + f(L2, B))

Where the pair (A, B) is being one of the (L1, R2), (L1 + 1, R2), (L1, R2 - 1) or (L1 + 1, R2 - 1).

And now the update is done by simply updating a leaf's node and the nodes from it to the root resulting in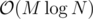 complexity. The answer after each update will be the maximal of the 4 values for the root node.

PS: This solution works only if for every i, ai ≥ 0.

PS2: f(x, x + 1) = 0 for every x as we cannot chose 2 adjacent elements.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Thanks a lot. I'll try to solve the problem with your idea.

    → Reply
  • »
    »
    3 weeks ago, # ^ |
      Vote: I like it -14 Vote: I do not like it

    yo this saved me big time during this leetcode contest

    → Reply
  • »
    »
    3 weeks ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    PS: This solution works only if for every i, ai ≥ 0.

    Why is this the case? In any case, we can treat negative a[i] as just zero since it's always better to discard negative numbers. But the original solution seemed to work regardless of whether a[i] is positive or negative.

    → Reply