I've recently come across the following problem in a real life scenario:
You are given a regular expression with two special characters: * matches any sequence of characters (including the empty sequence) and ? matches any one character.
For example, a?b matches acb, but it does not match abc, accb or ab. a*?b however does match accb. abc*f?h matches abcdefgh.
You have to write a program that checks if a pattern and a string match.
Obviously, we can write an O(n^2) algorithm which looks like this:
bool matches(const char *pat, const char *s) {
if (*pat == 0)
return (*s == 0);
if ((*pat == '?' || *pat == *s) && (*s != 0))
return matches(pat + 1, s + 1);
if (*pat == '*')
return ((*s != 0) && matches(pat, s + 1)) || matches(pat + 1, s);
return false;
}
For the scenario I have encountered, O(n^2) is more than enough, however I've been wondering for a while if a linear time algorithm (or anyway something better than quadratic) exists. I've been giving it some thought and can't seem to come up with anything. It looks like so it seems like some linear algorithm should exist, right?











According to http://publications.csail.mit.edu/lcs/pubs/pdf/MIT-LCS-TM-041.pdf, it is possible to solve the problem involving only characters and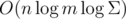 (where n is the length of the text, m is the length of the pattern, and Σ is the alphabet size).
(where n is the length of the text, m is the length of the pattern, and Σ is the alphabet size).
?in timeA way to solve the full problem is to split the pattern in blocks separated by
*. Then, we can loop over blocks, search for the first occurrence of each block in our text, and remove all characters that are before or inside that occurrence.In order to obtain a subquadratic algorithm, we need to be able to find the first occurrence of a pattern with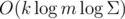 , when the pattern is matched in the first k characters of the text. To do so, it is enough to use the offline algorithm for the first 1, 2, 4, ... characters of the text, until the pattern is matched or we know that the pattern is not matched in the whole string.
, when the pattern is matched in the first k characters of the text. To do so, it is enough to use the offline algorithm for the first 1, 2, 4, ... characters of the text, until the pattern is matched or we know that the pattern is not matched in the whole string.
?in timeThe resulting algorithm for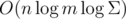
?and*should work in timeThis seems like it should work.
I don't really understand the part about using "the offline algorithm" (since our text changes (by removing characters from the start) after every token I don't see how we can do offline computations), but at any rate you can do binary search which I think would bring the complexity to
O(n logn logm log(sigma)), which is still sub-quadratic.Please note that I haven't read the linked paper (only the abstract and a few lines).