It is well known that given points (x, y) and you need to calculate the Manhattan distances between them, instead of using |x1-x2|+|y1-y2| you can first convert all points (x, y) into (x+y, x-y) and the distances will become max(|x1-x2|, |y1-y2|) (also known as Chebyshev distance). Can this trick apply to higher dimensions?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 02:46:02 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Oh, interesting trick. Can you give me a link to a problem that can be solved using this trick?
https://code-festival-2017-quala.contest.atcoder.jp/tasks/code_festival_2017_quala_d https://www.codechef.com/problems/TELEPORT
Codeforces Round #468 Div1D
Oh, thanks! I solved this problem, But it's not about max(|x1-x2|, |y1-y2|)
Actually it is.
sanya, luchshe sotku verni
Well, the unit circles in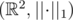 and
and 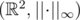 are both squares (although one of them rotated and shrinked by
are both squares (although one of them rotated and shrinked by 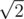 ) and therefore isomorphic as stated in the question.
) and therefore isomorphic as stated in the question.
But, the unit circle in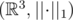 is an octahedron, while the unit circle in
is an octahedron, while the unit circle in  is just a regular cube. I don't see an elementary formal proof that this implies that there isn't a bijection with wanted properties in dimensions higher than 2, but intuitively it seems that this is the reason the trick doesn't work in higher dimensions.
is just a regular cube. I don't see an elementary formal proof that this implies that there isn't a bijection with wanted properties in dimensions higher than 2, but intuitively it seems that this is the reason the trick doesn't work in higher dimensions.
That's a nice way to see it! Maybe someone who deals with topology can help here? There may be some kind of non-trivial isomorphism between the 2 spaces (not exactly the aforementioned manhattan distance one).
IOI 2007 pairs. As I can remember, to solve this problem you should consider 4D space. Transform point (x, y, z) to the point (x + y + z, x + y — z, x — y + z, -x + y + z).
nice trick!! but do you have any proof for that? I thought about it but nothing came to mind
suppose you have been given two 2-dimenstional points $$$(x1,y1)$$$ and $$$(x2,y2)$$$
in the new coordinate system these points become $$$(x1 + y1, x1 - y1)$$$ and $$$(x2 + y2, x2 - y2)$$$
for convenience let $$$a1 = x1 + y1$$$, $$$b1 = x1 - y1$$$, $$$a2 = x2 + y2$$$ and $$$b2 = x2 - y2$$$.
the points in the new coordinate system are $$$(a1, b1)$$$ and $$$(a2, b2)$$$
we have to prove that $$$|x1 - x2| + |y1 - y2| = max(|a1 - a2|, |b1 - b2|)$$$
Consider the $$$RHS$$$
$$$RHS = max(|a1 - a2|, |b1 - b2|)$$$
substituting the values for $$$a1, a2, b1, b2$$$ we get
$$$RHS = max(|(x1 + y1) - (x2 + y2)|, |(x1 - y1) - (x2 - y2)|)$$$
$$$RHS = max(|(x1 - x2) + (y1 - y2)|, |(x1 - x2) + (y2 - y1)|)$$$
to simplify this let $$$n = x1 - x2$$$ and $$$m = y1 - y2$$$
We get $$$RHS = max(|n + m|, |n - m|)$$$
We can also rewrite the $$$LHS$$$ in terms of $$$n \text{ and } m$$$ as $$$LHS = |n| + |m|$$$
Now we have to prove $$$|n| + |m| = max(|n + m|, |n - m|)$$$
This can be proven by considering the four cases
case 1. $$$n >= 0, m >= 0$$$
case 2. $$$n < 0, m >= 0$$$
case 3. $$$n >= 0, m < 0$$$
case 4. $$$n < 0, m < 0$$$
thanks, this helped me a lot XD