What Mo's algorithm essentially does is this:
Given a set of q points in the plane, where the i-th point is (xi, yi) and 1 ≤ xi ≤ yi ≤ n, find a permutation of those points such that 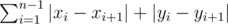 is minimized. So, the first question is this:
is minimized. So, the first question is this:
Does Mo's algorithm give us the optimal solution for this problem, or just an approximation of the optimal solution? The first problem is somewhat similar to the rectilinear (Manhattan distance) travelling salesman problem.
The second question is this: If Mo's algorithm actually gives us an approximation of the optimal solution (which seems to be the case), how much better is the optimal solution? (i.e. let's assume that the total distance in Mo's algorithm is x, and the total distance in the optimal solution for some set of points is y. What is the greatest value of y - x or  ?) Also, what are some interesting observations about the optimal solution?
?) Also, what are some interesting observations about the optimal solution?
Question 3: What's the best algorithm that gives an exact solution to the first problem?










Auto comment: topic has been updated by f2lk6wf90d (previous revision, new revision, compare).
Auto comment: topic has been updated by f2lk6wf90d (previous revision, new revision, compare).
I'm not sure on how to apply Mo's algorithm to this problem. I believe the classical application is to find the most frequent element in an interval. As for the problem you described, I can't think of any solutions other than the TSP... maybe there is a solution similar to the JOI 2016 — Skyscraper problem, though I'm not so sure.
By Mo's algorithm, I mean the well-known comparator
return (l1 / BLOCK_SIZE) < (l2 / BLOCK_SIZE) || ((l1 / BLOCK_SIZE) == (l2 / BLOCK_SIZE) && r1 < r2);. It is obvious how this gives an approximation to the solution to the first problem.It gives optimal solution for worst instance of given problem. Consider O(n) points with coordinates of form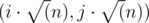 . Distance shortest distance between pair of points is
. Distance shortest distance between pair of points is 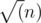 , so minimum value of the function above is
, so minimum value of the function above is 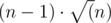 and MO will find solution like that. In other cases MO will find permutation with cost that not worse than optimal solution for worst case, but maybe worse that optimal solution for given case.
and MO will find solution like that. In other cases MO will find permutation with cost that not worse than optimal solution for worst case, but maybe worse that optimal solution for given case.
if you change your compare function to bellow, you will get answer about 2 times faster:
you can see this with compare this submissions
1.35150789 : 1216 ms
2.23682619 : 2246 ms